Linear Algebra 6. Determinant

determinant https://youtu.be/Ip3X9LOh2dk?si=BoU2eib6WvVzoQCD

linear transformation을 사용하다보면 공간을 찌그러뜨리거나 늘리고 있다는 것을 느낄 수 있는데 이와 관련된 정량화 된 값이 determinant이다.

• 특정 지역의 크기를 증가/감소 시키는 factor(요인)값을 측정해보는것!
• unit square이 기준일 때 2차원 영역에서는 넓이가 얼마나 증가했냐를 측정

Determinant

2차원과 3차원이든 상관없이 scaling이 얼마되었는지를 보여주는 factor로 차원이 다를 때는 단지 scaling되는 것의 차원이 올라가고(넓이→ 부피) ,negative value를 가질때의 기준이 달라진다.(오른손 법칙)

2-Dimension

---

linear transformation에 의한 영역(area)의 변화를 나타내는 factor

• determinant=3: unit square영역의 넓이가 3배 증가한다고 생각!
• determinant=0: 넓이의 크기가 0배되게 만드는 factor이므로 선, 점이 된다는 것을 의미한다.

이때 determinant는 negative value(음수 값)도 가진다. 이때 음수는 다음과 같은 성질을 의미한다

• 방향(orientation)과 밀접한 관게! (설명하는 여러가지 방법)

1. 공간이 flip될 경우 음수값 = invert of tranformation space
2. basis vector을 이용해 이 vector의 순서가 유지되는지
   • $\hat{i}$이 $\hat{g}$ 오른쪽에 있다가 변환 후 왼쪽으로 이동했다면 invert가 된 것으로 보고 음수값을 갖는다.
   • 이렇게 순서가 바뀌도록 transformation을 생각해보면 공간이 flip됐다는 것을 직관적으로 느낄 수 있음

• 절댓값 자체는 scaling에 관한 정보를 담고 있음

3-Dimension

---

unit cube(1X1X1)를 기준으로 부피가 얼마나 변할지를 알려주는 scaling factor가 determinant가 된다

• determinant=0 : 하나의 면적, 선, 점이 되는 것으로 차원 축소가 이뤄질 때 나타난다.
  • 이는 곧 vector들이 부피를 만들지 못하며linearly_dependent 한다는 것을 의미한다ㄷ
  • Linear Algebra 2. Linear combination, span and basis vectors

negative value는 어떤 기준으로 결정될까? 이것 역시 방향과 관계가 되어있으며 flip될 경우 음수 값을 가진다고 볼 수 있다

• 오른손법칙= 검지: $\hat{i}$, 중지: $\hat{j}$, 엄지: $\hat{k}$
• 변환 이후에도 방향이 똑같으면 +, 왼손으로 가능하면 방향이 flip된 것이므로 -값을 가진다

Compute Determinant

$det([a,b],[c,d])=ad-bc$(2차원)

• 만약 b와 c가 0이라면 각 좌표는 basis vector위에 있게 되고 곧 직사각형의 넓이와 같게 됨(det=ad)
• 만약 b와 c 중 하나만 0이라면 평행사변형의 넓이를 구하는 것과 같게 됨(det=ad)
• 만약 b와 c 모두 0이 아니라면 bc는 대각선 방향으로 얼마나 늘려지거나 찌그러지는지를 알려줌
  • 이때는 신발끈 공식을 생각하면 됨!

Sal khan 동영상에 determinat 계산방법이 자세하게 나와있으며 아래는 3차원일때 determinant 구하는 방법

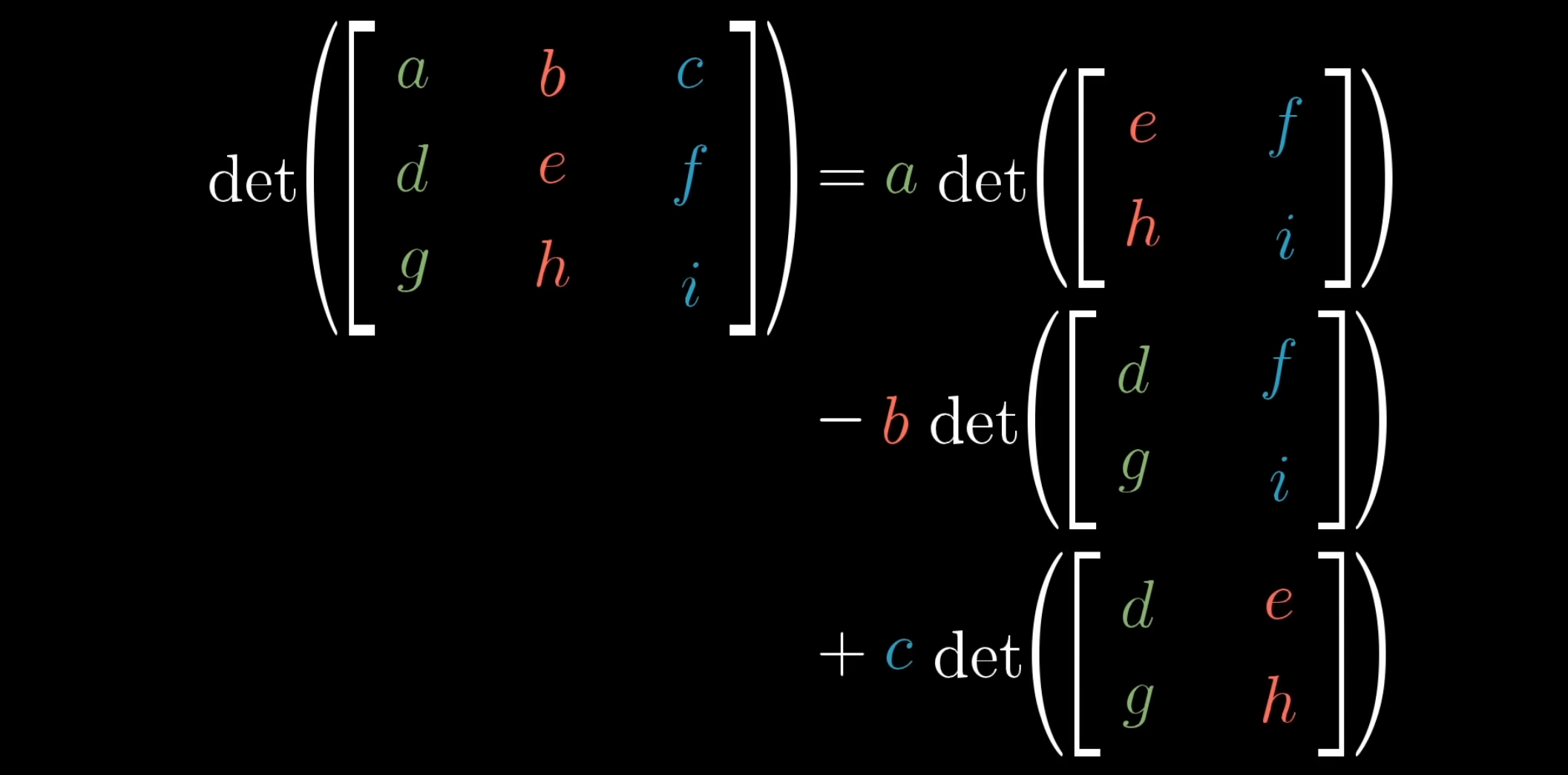
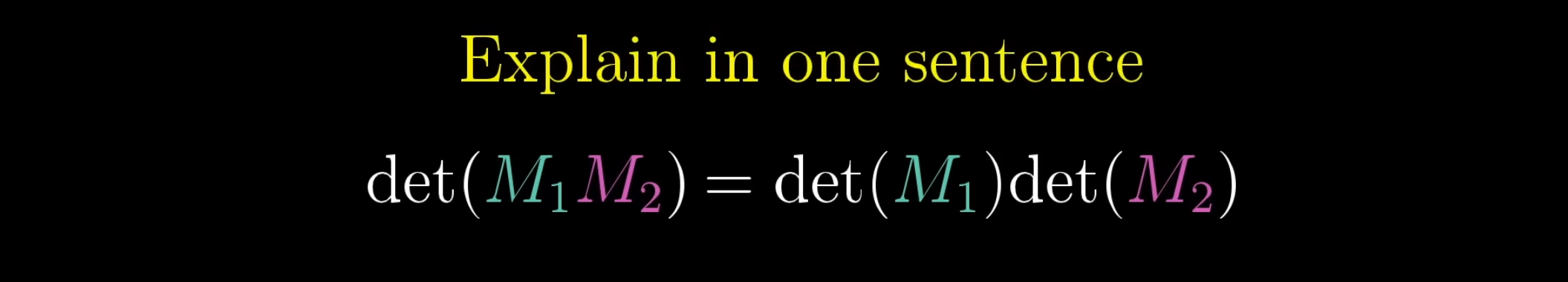
• [?] 왜 그럴까?