🪴 Quartz 4.0

Search

SearchSearch

CS231n 5. Convolutional Neural Network (CNN)

Dec 22, 202421 min read

Question

https://velog.io/@cha-suyeon/cs231n-5강-정리-Convolutional-Neural-Networks 정리 잘해놓은 블로그!

기존 Multi-layered neural network(MLP)가 가지고 있던 문제점은 다음과 같다.

  1. weight와 input간의 연산을 진행할 때고차원의 input 이미지 정보를 1차원으로 바꿔 데이터의 형상을 무시함
  2. weight(parameter)의 수가 매우 많아져 모델의 복잡도가 증가하고 일반화 능력이 떨어져overfitting 가능성 올라감 (항상 큰 크기의 weight를 이용하며, 이를 최적화하는데 오랜 시간이 걸림
  3. 기존의 input이 조금만 바뀌어도(이미지가 회전하거나 크기가 달라질 때) 새로운 데이터로 인식하여 학습을 다시해야하고 일반화 능력이 떨어짐 (물론, feature transformation으로 어느 정도 해결할 수도 있지만 한계가 존재함)

CNN이란?

기존 classifier과 neural network와 다른 점은 ConvNet의 layer들이 3차원의(width,height,depth) 뉴런으로 이루어져 input data의 spatial structure을 유지하며 학습한다는 것이다. (기존에는 하나의 긴 vector로 만들었음) 즉, 각 layer은 3차원 volume을 입력으로 받아 미분 가능한 함수를 거쳐 다시 3차원 volume을 출력한다. 이때 각 layer의 뉴런들이 input의 특정 지역(small region)과 연결되어 이 부분만 학습을 진행한다.

이런 기술이 나오게 된 역사를 간단하게 살펴보면 다음과 같다

  1. 고양이 실험에서 시각 피질 안에 많은 뉴런이 local receptive field를 가진다는 것을 알게 되었다. 즉, 하나의 neuron이 들어온 시각 데이터의 일부분만을 특정하여 담당한다는 것이다
  2. 이때 receptive field는 겹쳐질 수 있고 곧 전체 시야를 이루는데 고수준의 뉴런이 이웃해있는 저수준의 neuron의 출력에 기반한다
  3. 뉴런은 계층구조를 가짐: 이 아이디어를 이용해 컴퓨터 비전에서 활용하였으며 이때 구조에 깊은 부분에 들어감에 따라 이미지의 간단한 구조인 전체적인 선등에 반응하다가 점점 모서리의 더 끝점에 반응하게 됨을 통해에 계층적 구조로 된 것을 다시 확인할 수 있었다

왜 "Convolution"인가?

convolution은 해석하자면 합성곱이라는 의미로 두 함수나 신호를 결합해 새로운 함수를 만들어내는 과정을 의미한다. 이때 수학적의미와 컴퓨터에서 사용하는 의미가 서로 다르다.

  1. 수학적 정의: 두 함수 와 가 있을 때 두 함수 중 하나는 고정된 상태로, 다른 하나는 뒤집혀서 이동하는 동안 두 함수가 겹치는 부분의 값을 적분하는 과정
  2. 딥러닝에서의 정의: 여기서는 수학적 정의와는 다르게 뒤집다에 초점을 두기보다는 겹치는 값을 결합에 초점을 두어 image와 filter 사이의 연산을 한다는 것을 의미한다

Parameter sharing

spatial structure을 유지한다는 CNN의 특징 이외에도 중요한 특징이 있다. 바로 parameter sharing으로 동일한 계수(weight)를 갖는 filter가 같은 layer에서 똑같이 반복적으로 이용되는 것이 특징이다. 이 filter의 결과는 이동할 때마다(sliding) 하나의 단일 값을 만들어내어 이것들의 모음이 activation map의 하나의 depth가 된다.

이를 통해 다음과 같은 장점을 가지게 된다.

  1. parameter의 수가 줄어듦 ⇒ 만약 filter을 반복적으로 사용하지 않는다면 parameter의 수가 input의 면적만큼 커져 이전에 classifier와 크게 다른점이 없게 된다
  2. 위상(topology)와 무관한 값을 학습: 같은 filter의 값으로 계산하기 때문에 일반화 능력이 상승하며 이는 input 이미지의 지역적 특징을 감지하고 학습을 통해 전체 일반적인 패턴을 학습하여 variation이 생겨도 동일한 것으로 분류할 수 있게 되기 때문이다 (하나의 neuron이 input의 특정한 부분과 연결되어 그 부분만 학습을 하게 됨)
  3. 재사용 가능: 학습 후에 어떤 부분이 중요하다고 감지할 경우, 이 filter을 가지고 학습이 가능하므로 성능이 올라갈 수 있다.

참고로, input data의 공간적 구조는 유지가 되지만 filter가 돌아다니면서 내적연산을 하는 것을 실제로 구현할 때는 filter를 하나의 긴 vector로 펼쳐 계산하게 된다.(그럼으로써 하나의 값을 만들어내고 이것을 반복적으로 진행하여 결과적으로 공간적 구조는 유지됨)

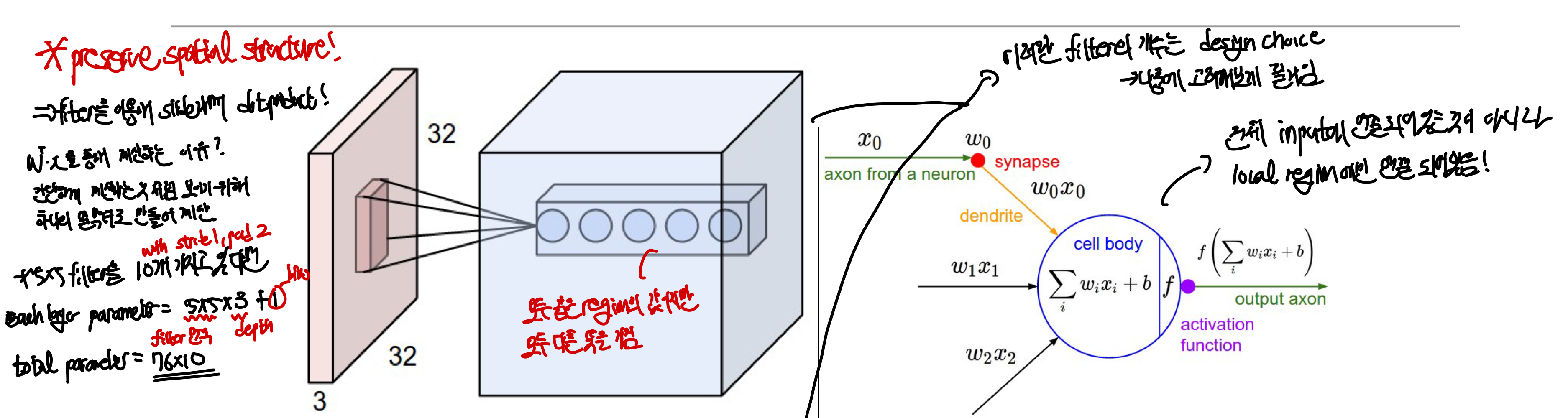
Convolutional Layer

CNN에는 여러가지 layer들이 존재하는데 그 중에서 가장 특징적이고 중요한 것이 바로 Convolutional Layer이다. 이 Convolution layer에서 어떻게 forward pass가 이루어지고 학습이 진행되는지는 다음과 같은 과정을 통해 이루어진다.

  1. 내적 진행: forward pass를 하는동안 filter가 input의 공간속을 slide를 하면서 filter의 parameter값과 input의 값 사이에 내적을 진행한다.
  2. activation map 생성: 각 layer의 결과값을 통해activation_map 을 만든다. 이때 activation이란 nueron(특정 위치에서의 내적 값)이 fire을 한 정도를 나타내며, 이 내적한 값이 클 수록 그 부분의 데이터를 많이 활용한다고 보면 된다. 결국 어느 부분이 분류하는데에 활용이 잘되는지를 기록한다고 생각하면 된다.

activation map의 특징

이때 한 layer에서 여러가지 filter들을 이용해 activation map을 사용하게 되는데 이렇게 함으로써 각각의 filter가 특정한 template이나 특징들을 알 수 있게 만든다.

➡️ activation map의 차원이 많은 이유+ linear classifier에서 w의 크기가 매우 컸던 것과 유사하게 여기서는 w의 크기는 작지만 여러개를 사용한다고 생각하면 되며 이때 filter의 개수는 사용자의 선택에 따라 달라지게 된다

이때 input의 depth가 존재하므로 filter 역시 input의 depth와 같은 크기의 depth가 존재해야한다. 만약 32x32X3 input에 5X5 filter을 사용하기위해서는 filter가 5X5x3이어야 하며 filter 6개를 사용하게 되면 activation map은 28X28X6이 되어 depth가 6이 된다`

  • 참고로 최근의 트렌드는 작은 filter들과 깊은 모델 구조라고 한다
  1. 과정 반복: 최종적으로 activation map은 다음 layer의 input이 되어 이 과정을 반복한다.
    • 예를 들어 5개의 filter가 있다면 output depth volume은 5가 된다.
    • 모두 같은 region을 학습한 값이지만 filter마다 parameter가 달라 activation map안에 있는 각각의 neuron들은 다른 값을 가진다
    • 결국 기존의 classifier은 input의 모든 영역을 보고 그것을 하나의 output으로 만들어냈다면, CNN에서는 input의 특정 영역만을 이용해 output을 만들어낸다는 뜻으로 이렇게 만들어진 activation map이 다시 input으로 들어가게 된다.

이때 input과 가까운 얕은 layer들은 주로 간단한 low-level feature(단순한 모서리, 선)들을 학습하게 되는 반면에 output가 가까운 깊은 layer들은 주로 복잡한 high-level feature(모서리, 선들의 조합)들을 학습하게 된다. 즉, 앞에서 언급한 계층구조를 활용한 것을 알 수 있다. 이때 아래 이미지는 neuron이 input image에서 어디를 보고 있느냐라고 생각하면 된다

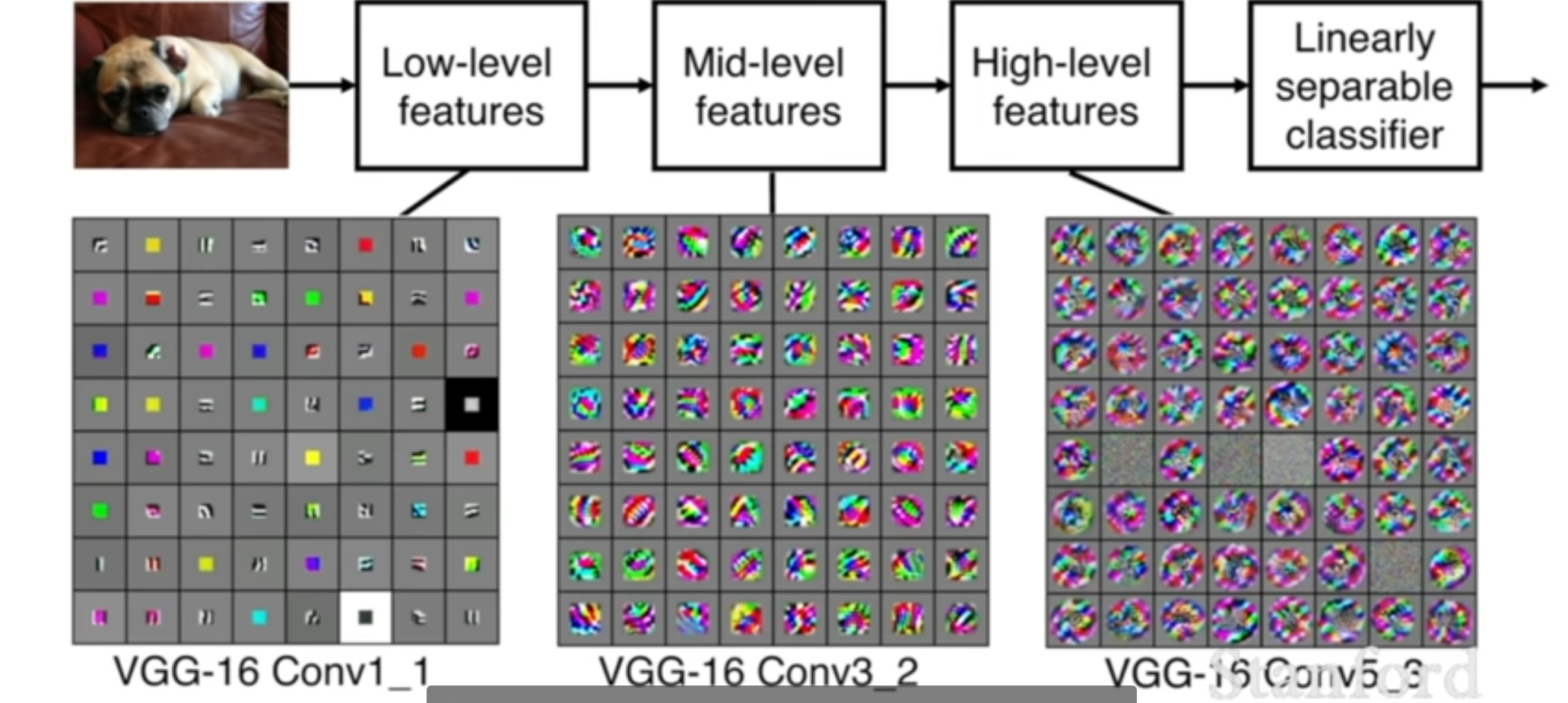
Local Connectivity (Locality)

Convolutional layer의 또 다른 특징은 바로 Locality이다. Locality란 픽셀을 주변 픽셀값과 비교하여 정보를 추측할 수 있는 특성을 말한다. input 이미지의 픽셀은 일관된 순서를 가지는데, filter을 통해, 이 filter의 receptive field만큼의 픽셀들과의 연산을 통해 단일한 값을 내기 때문에 인접한 픽셀끼리 영향을 준다는 것을 확인할 수 있다. 이 점이 모든 픽셀마다 독립적인 weight를 가져 주변 픽셀값과 독립적인fully connected layer와의 차이점이다.

Spatial arrangement

Convolutional layer이 어떤 특성을 가지고 있고 어떤 hyperparmeter가 있는지 알아보고, 이것들이 CNN의 영향을 어떻게 미칠지 알아보고자 한다.

  1. depth: Convolutional layer에서 depth는 몇개의 filter을 사용했는지를 의미한다.
    • 같은 depth column의 뉴런들은 input 이미지에 동일한 영역과 연결되어 있지만, 각 filter의 parameter들이 달라 각각 무엇을 의미하고 중점적으로 보는지는 다르다.
    • 예를 들어, 기존의 input의 고 이때 8개 filter을 이용해서 layer을 구성했을 경우, output은 이 된다.
  • [!] depth를 얼마나 할지는 몇개의 filter가 있어야지 학습이 온전히 가능할지에 대한 여부와 관련이 깊다. 너무 depth가 깊어지면 parameter의 수가 늘어나고, 너무 얕아지면 학습이 온전히 가능하지 않을 수 있다.
  1. stride: filter을 slide하는 정도를 정하는 것으로 이때 input에 따라 가능한 stride가 정해져 있다.(stride만큼 움직였을 때 input이 남거나 가지 않은 부분이 있으면 안됨)
    1. 해상도와 관련이 있으며 이것을 통해 output volume의 조절이 가능하다.
      • stride가 크면:downsample 의 효과 & activation map의 size를 줄임
      • stride가 작으면: output volume의 크기가 상대적으로 크게 됨
    2. downsample의 한가지 방법이 됨!
    3. 이때 가로와 세로의 stride값을 다르게 해도 상관없지만 (ex: 3X5 stride) 가로,세로가 같은 stride를 사용하는 것이 일반적이다. (주로 input도 정사각형인 경우가 많다)
  • [!] stride를 어떤 값으로 정할지는 때에 따라 다른데 1) down sample을 원하는지에 대한 여부 혹은 2) 전체 parameter의 수를 줄이는 것과 성능 사이에 trade-off(stride가 작아지면 parameter 수는 줄지만 단순해져 성능이 나빠질 수 있음)등을 고려해야한다.
  1. zero-padding: 입력데이터 주변을 특정값으로 채워서 늘리는 방법으로 꼭 0으로 채울 필요는 없지만 0으로 채우는 것이 자주 사용되는 방법으로 알려져있음
    1. input volume의 공간적 크기를 유지하기 하여 input data를 온전히 활용해 학습을 할 수 있게 만든다.
      • CNN 특성상 layer을 거쳐갈 수록 downsample이 되는경향이 있는데 이를 방지(특히 딥러닝에서 심각해질 수 있음!)
    2. 가장자리의 정보를 잃지 않기 위함
      • 가장 자리 부분은 filter가 연산되는 횟수가 가운데에 비해 적어가운데 값만 집중될 수 있음
      • 가장 자리에 있는 중요한 정보를 잃지 않기 위해서 필요함
    3. 이때 주로 padding하는 개수는 stride가 1일 때 공간의 사이즈를 지키기 위해 를 filter size라고 했을 때 를 사용한다.
  • [!] zero-padding을 언제하는지 역시 때에 따라 다른데, 만약 deep learning에서 input data를 온전히 활용하고 가장자리의 정보를 잃지 않고 싶다면 사용할 수 있지만 , 반대로 일부러 downsampling을 노려 zero-padding을 하지 않을 수도 있다.

Activation Map의 크기 구하는 법

  1. 한 layer에서 각각의 filter가 몇번 이동하게 되는지 구하기
  • [!] : input 사이즈, : receptive field 크기(fiter 크기), : stride의 크기, : 사용된 padding의 수

이때 는 x축으로 filter가 몇번 이동하면서 연산을 하는지에 대한 크기이며 만약 input이 정사각형이라면 총 연산의 횟수는 가 된다. 만약 값이 정수가 아니라면 불가능한 경우로 stride나 padding의 수를 바꾸어야 한다. 이때 와 는 정해져 있는 값임!

  • 가 주어졌을때 input volume을 똑같이 만들기 위해 P값을 조절하는데 쓰임
  • 가 주어졌을 때 가능한 S의 값을 계산하는데 쓰임
  1. Parameter Sharing을 사용할 때 사용되는 parameter의 수 구하기
  • [!] : receptive field size ,: depth ,: filter(layer)의 개수= , : bias의 개수

Pooling Layer

CNN에서 또 다른 layer에는 pooling layer가 존재한다. 이 layer은 출력값에서 일부분만을 추합하는 일종의 sub sampling으로downsample 의 효과를 얻어 input의 size를 줄이는 역할을 한다.

특징으로는 다음과 같다.

  • activation function을 거쳐 나온 출력 map을 압축하는 하여 크기를 줄이는 역할을 하며 이때 depth의 크기는 변하지 않는다. 예를 들어 2X2자리 pooling layer을 사용할 경우 75%가 날라가고 25%만 남게된다
  • filter을 곱해 값을 구하는 것이 아니라 평균/최댓값을 뽑아 사용하기 때문에 parameter가 없다
  • 가장 자리값을 채울 필요가 없기 때문에 padding을 하지 않는다
  • [!] pooling하는 것 역시 design choice! 너무 pooling을 많이하게 되면 간단해지지만 기존 image 데이터의 정보가 사라지며 주로 사용하는 setting은 & 혹은 & 이다.
  • [!] 다만 최근에는 pooling대신에 stride를 이용해 downsample을 하는 경우가 많아졌다

결국 pooling layer을 사용하는 이유는 1) spatial size를 줄이고 2) parameter의 수를 줄임으로써 연산의 양과 시간을 줄이고 3) overfitting의 정도를 조절할 수 있기 때문이다

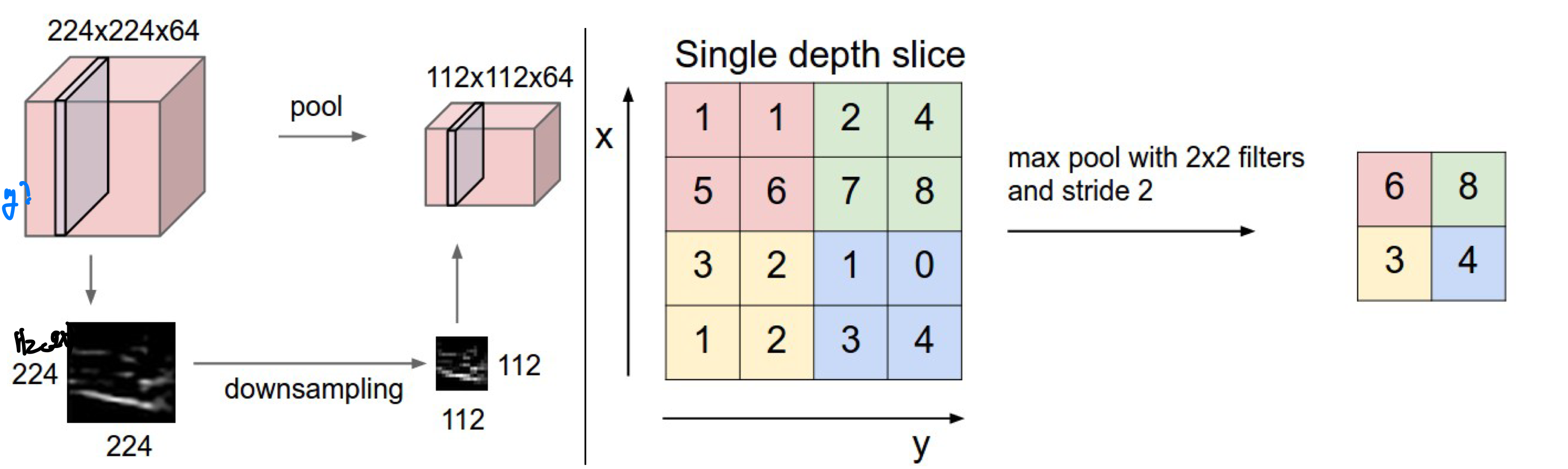
주로 max pooling을 하는 이유?

예전에는 average pooling이 많이 사용되다 현재는 max pooling이 자주 사용되고 있다. 현재 max pooling을 사용하는 이유는 결국 우리가 알고자하는 것은 image의 어떤 지역에서 뉴런이 fire가 많이 됐는지, 즉 학습을 하는데에 어떤 부분이 가장 주요하게 사용이 되었는지이기 때문에 max를 사용한다. 즉,

  1. 학습을 하는데에 사용되는 정도를 확인하는 것이 중요하기 때문에 max를 이용하는 것이 더 나은 선택
  2. backpropagation 에서 max의 gradient는 forward pass에서 높은 값과 같아 연산이 쉬움 의 이유로 주로 사용이 된다

CNN의 사용(예제)

Covnet은 여러가지의 layer들로 이루어져있는데 이 layer들이 모여 하나를 이루게 된다

  1. Input layer: 원본 이미지 그 자체이며 32X32X3으로 이루어져있음(color channel이 3개여서 depth=3)
  2. CONV layer: input의 local region과 연결되어 내적을 이용해 결과를 저장 32x32X12(12개 filter 사용)
  3. RELU layer:activation_function 을 사용하는 부분으로 volume size는 일정하다
  4. POOL Layer: spatial dimension을 downsampling을 하는 역할을 함 16X16X12. 결국 RELU의 결과가 POOL layer에 들어가는데 단지 downsampling만 했기에 크기가 달라지고 사진의 형태는 비슷하게 유지된다
  5. FC Layer: 전에 다뤘던 layer로 더 이상 공간 정보를 유지하지 않고 class score을 계산하기 위해 사용된다

Aside

ConvNetJS demo: traing on CIFAR-10 activation에 대한 직관을 얻을 수 있음 https://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html 처음에는 그냥 모서리를 확인할 수 있다가 나중에는 정확히 코너를 찾는 것과 같이 layer가 깊어질 수록 더욱 더 복잡한 것을 발견 가능하다. 다만 activation map을 보게 되면 처음에만 사람이 이해할 수 있는 형태가 되고 그 후에는 사람이 보기에 어떤 의미가 있는지 확인하기 어렵다

Graph View

Backlinks