CS229 9. Approx, Estimator Error & ERM

이번 강의에서는 머신러닝이 어떻게 작동이 되는지 그 속을 살펴볼 것이다, 또한 어떻게 variance와 bias를 바라볼지와 이를 통해 error를 어떻게 줄일 수 있을지 수학적 개념과 함께 살펴볼 것이다. 그 전에 머신러닝에 깔려있는 가정(assmption)에 대해서 알아보자!

Assumption

CS229에서 다루는 대부분의 알고리즘은 다음과 같은 가정을 따르고 있다.

1. Data distribution D, (x , y) ~ D

즉, 지난 8강에서 언급했다싶이 training set과 test set 모두 같은 distribution을 가진다는 뜻이다. 이는 supervised learning과 unsupervised learning 알고리즘 모두에게 적용되며 이 가정이 없다면 data generating process(학습과정)에서 모델이 굉장히 복잡해지거나 학습이 매우 힘들어진다.

2. Independents Samples

Data distirbution에서 sample한 subset들끼리 서로 independent하다.

Data generating process

Data가 어떻게 sample되어 알고리즘을 거쳐 hypothesis를 만들어내는 일련의 과정을 의미하며 주어진 데이터가 어떻게 생성되었는지를 나타내는 모델이나 과정을 의미한다. hypotheis와 같이 모델의 예측값, 즉 random variable을 어떻게 생성할지에 대한 과정을 나타낸다고 생각하면 된다. 이에 대한 과정을 요약하면 다음과 같다. 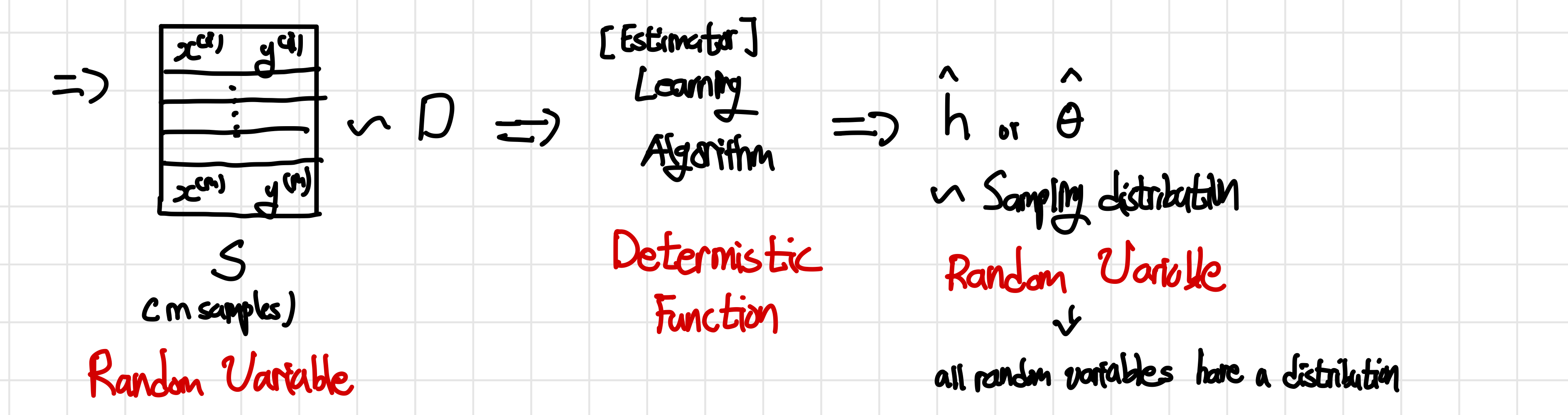과정을 간략하게 설명하면 주어진 data distribution D를 따르는 example에서 m개의 example을 sampling하여 이를 learning 알고리즘의 input으로 넣는다. 그리고 learning algorithm에 결과로 $\hat{h}$ ,$\hat{\theta }$가 나오게 된다.(x를 input으로 받아 y를 예측하는 $\hat{h}$이 나오는 것이 맞는데 만약 특정 알고리즘에 특정 hypothesis로 제한시키면 parameter $\hat{\theta }$를 구하는 것이 $\hat{h}$과 같다)

이때 assumption에서 나와있다싶이 input data에서 m개의 example을 sample할 때와 learning algorithm의 output 모두 같은 distribution을 공유하며 이때 이 두 경우 모두 특정 확률 실험의 결과(Sampling from distribution) random variable(변수는 특정한 값을 갖지만 어떤 값이 될지 예측할 수는 없음)인 것을 알아야한다. 다만 learning 알고리즘은 random variable이 아닌데 동일한 입력에 대해 동일한 출력을 생성하는 함수인deterministic_function 이기 때문이다.

여기서 learning 알고리즘은 지금까지 우리가 배웠던 여러 알고리즘이 될 수 있을 뿐 아니라 input data를 받아 output data를 내보낼 수 있는 deterministic function이면 모두 가능할 수 있다.

결국 이 data generating process에서 생각해볼 수 있는 것은 true parameter $h^{\ast }$ 과 ${\theta }^{\ast }$가 존재할 것이라는 것이다 (Frequenist 의 관점! CS229 8. Data Splits, Models & Cross-Validation ) 이때 $h^{\ast }$ 과 ${\theta }^{\ast }$는 learning 알고리즘의 output이 되길 바라는 parameter로 실제로 무엇인지 우리는 알 수 가 없다. 또한 이 값들은 probability distribution이 없기 때문에 random variable이 아니라 constant이다.

Frequenist 관점에서 바라본 data generating process

Frequentist 통계학은 데이터를 여러번 수집했을 때, 추정치가 얼마나 실제 parameter과 가까운지에 주안점을 둔다. 이런 관점에서 true parameter $h^{\ast }$ 과 ${\theta }^{\ast }$ 는 무한히 많은 데이터를 수집했을 떄 나타나는 진정한 parameter라고 생각할 수 있다

hat(^)과 star(*)의 차이

• hat(^): 우리가 직접 평가하거나 계산한 결과의 의미로 random variable이 된다
• star(*): true/ right answer을 의미하며 하나의 constant가 된다

Data view VS Parameter view

여기서는 8강에서 배웠던 bias와 variance를 각각 데이터가 축이 되는 data view와 parameter가 축이 되는 parameter view(관점)에서 새롭게 다시 확인하고자 한다. 이를 통해 bias와 variance를 더 보기 좋게 시각화하고 이해를 도우며, 후에 나올 estimator error를 직관적으로 이해할 수 있게 될 것이다. CS229 8. Data Splits, Models & Cross-Validation

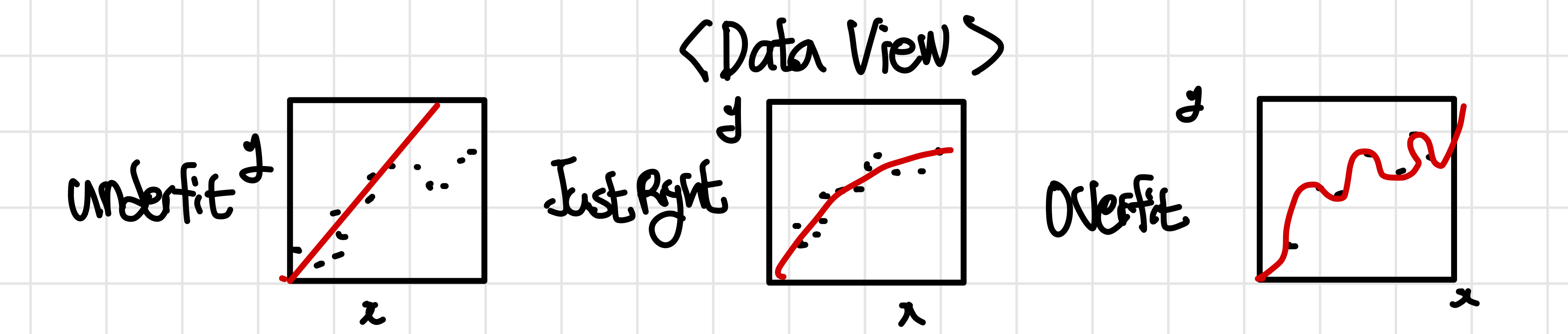
이는 우리가 underfitting과 Overfitting과 관련해서 공부를 할 때 자주 봤던 관점으로 Data들의 관점들을 통해 bias와 variance가 어떤 형태인지 알아보는 방법이다.

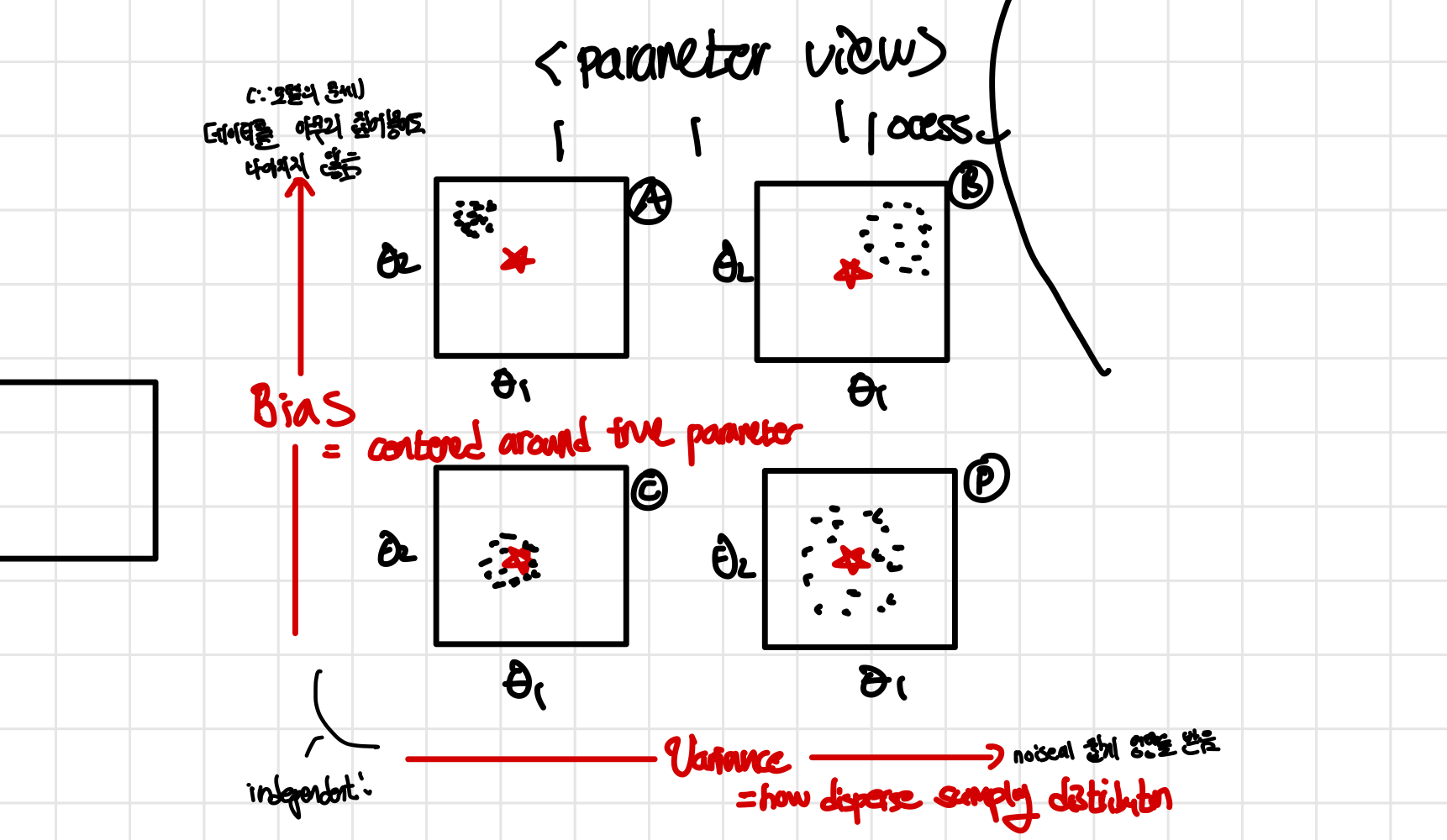
이는 parameter($\theta$) view로 bias와 variance가 어떤지 알아보기 더 쉬운 관점이다. 이때 bias는 실제 true parameter star’*(${\theta }^{\ast }or{h}^{\ast }$)에 얼마나 가까이 있는지를 나타내는 지표이고 variance는 sampling distribution이 얼마나 분산(disperse)되어있는지를 나타내는 지표이다. - dot(점) : distributiiobn에서 sampling한 결과 - dot(점)의 수 : experiment 수 (시행횟수)

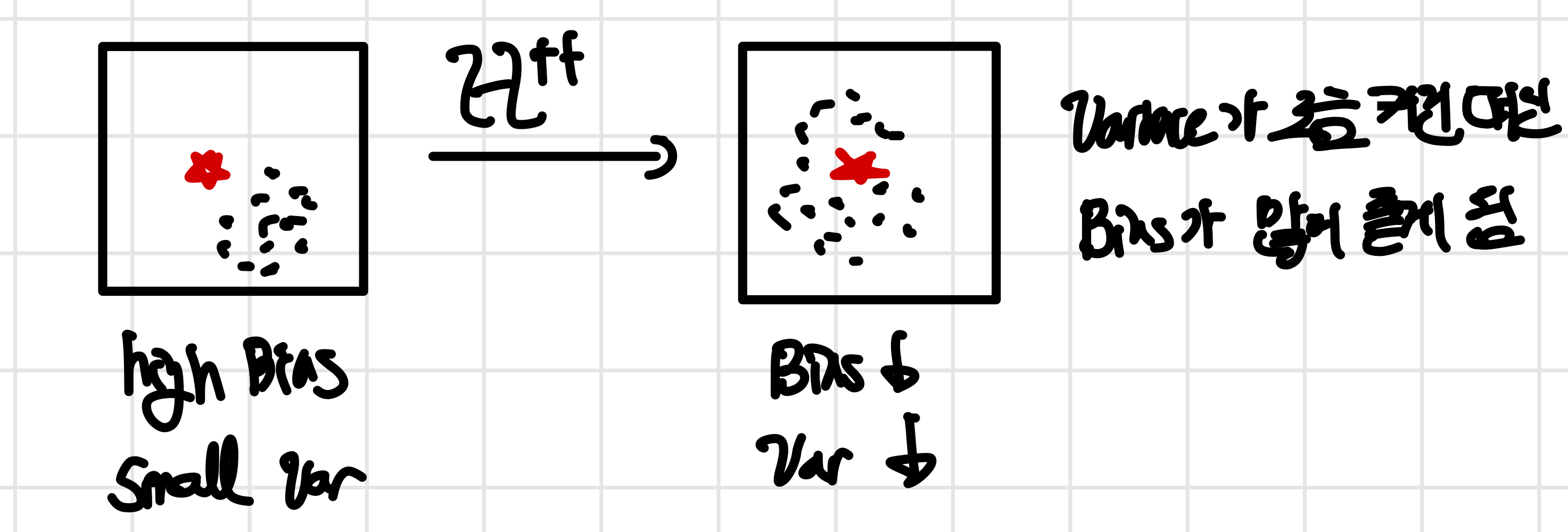
결국 bias가 높은 문제는 데이터를 아무리 집어넣어도 나아지지 않기 떄문에 모델이 문제가 되며 variance의 문제는 sample size m과 관려한 문제라는 것을 알 수 있다.

우리는 m개의 example을 sample하여 위 process를 진행하면 우리는 각 모델마다 $\hat{\theta }$룰 구할 수 있다

Statistical Efficiency 주어진 data에서 정보를 정보를 얻어 알고리즘이 얼마나 효율적인지를 나타내며 알고리즘에 따라 다른 값을 가진다.

• $m->\infty =>Var(\hat{\theta })\to 0$ : 즉, 한번에 sampling된 data의 수 (m)이 커질 수록 variance는 0에 가까워진게 된다는 뜻이다
• $m\to \infty ⟹\hat{\theta }\to {\theta }^{\ast }$ : 즉, 한번에 sampling data의 수가 무한대로 발산할 경우 한점(constant)로 모이게 되며, 그 한 점이 바로 true parameter ${\theta }^{\ast }$가 된다. (random variable에서 constant가 됨)
• 이 뜻을 조금 다르게 생각해보면 모든 m에 대해서 $E[\hat{\theta }]={\theta }^{\ast }$을 만족시킨다. (두 값 모두 constant)

참고로 sample size와 상관없이 sampling 분포가 true parameter에 있다면 unbiased estimator(algorithm) 이라고 한다.

결론적으로 여기서 variance는 sampling size m과 관련이 있다는 것을 알 수 있는데 과연 그 이유는 무엇일까? 그리고 이를 어떻게 증명할 수 있을까?

Fighting variance

variance 문제가 되는 부분은 high variance일 떄이다.이 경우에는 예측한 parameter들이 실제 parameter에 모여있지 않고 퍼져있는데 이럴 경우에는 sample을 할 때마다 hypothesis가 매우 달라져 overfiitng이 생길 수 있다. 이럴 때 해결하기 위한 방법은 다음 2가지가 있다.

1. m→ ∞ 즉, sample을 하는 example들을 늘려 한점을 예측하는 것으로, 이렇게 될 경우 각 sample을 할 때마다 겹치는 example들이 많아져 varinace가 감소하게 된다

2. regularization (L1, L2)

regularization을 통해 variance가 큰 경우의 penalty를 부여하여 varinace가 작아지도록 모델을 설계하는 방법이다. 다만 이럴 경우 bias와 trade off가 생기게 되는데 loss가 최소가 되지 않는 부분에서 최적의 값이 생기기 떄문에 true parameter와 조금 멀어지게 될 수 있다. 하지만 variance가 더 큰 비율로 문제가 된다면 bias를 조금 크게 만드는 대신에 variance를 많이 줄도록 만들어야한다.

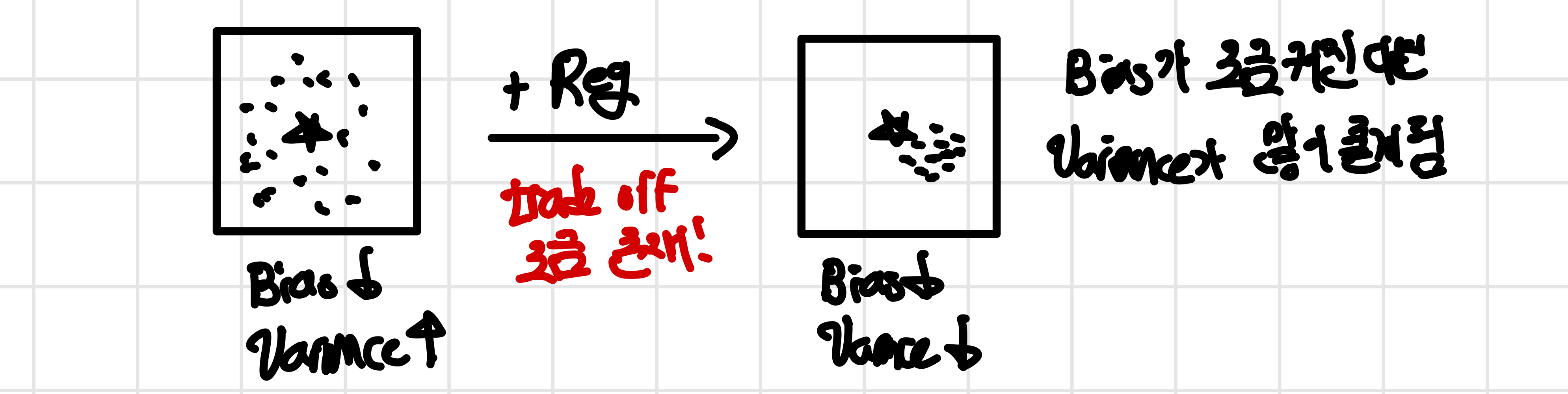
이를 뒤에서 언급한 hypothesis class와 연관지어 생각하면regularization 을 추가하게 될 경우 hypothesis class가 줄어들게 되어 일반적으로는 varinace가 줄고 bias는 늘어나게 된다. 다만 특별한 경우 영역이 마침 알맞게 줄어들게 될 경우 bias가 달라지지 않을 수도 있다. 이에 대해서는 estimator error와 함께 class of hypothesis를 배울 때 다시 언급하고자 한다.

Fighting bias

bias 여기서도 문제가 되는 부분은 bias가 큰 경우이다. 이럴 경우에는 가장 쉬운 한가지 해결방법이 존재한다

1. make H(class of hypothesis) bigger

뒤에서 언급할 hypothesis space와 연관이 되어 있는 내용인데 hypothesis class를 늘리게 되면 최적의 hypothesis($\hat{h}$)가 true parameter 혹은 best hypothesis($h^{\ast }$)에 가까워지게 되어 bias가 작아지게 된다.

다만 hypothesis class가 커지게 될 경우 가능한 hypothesis의 개수가 늘어나게 되어 (넓어져서 다양한 값 나옴)variance는 증가하게 된다. 그렇기 때문에 Fighting variance와 같이 Bias가 더 큰 비중으로 문제가 되는 경우에 variance가 조금 증가하고 bias는 많이 줄어들게 만들어 bias 문제를 해결할 수 있다.

Estimator Error

이제부터는 위에서 확인했던 bias와 variance를 해결하는 방법이 왜 타당한지에 대해서 class of hypothesis의 개념과 estimator/generalization error을 통해 설명할 것이다!

Space of Hypothesis

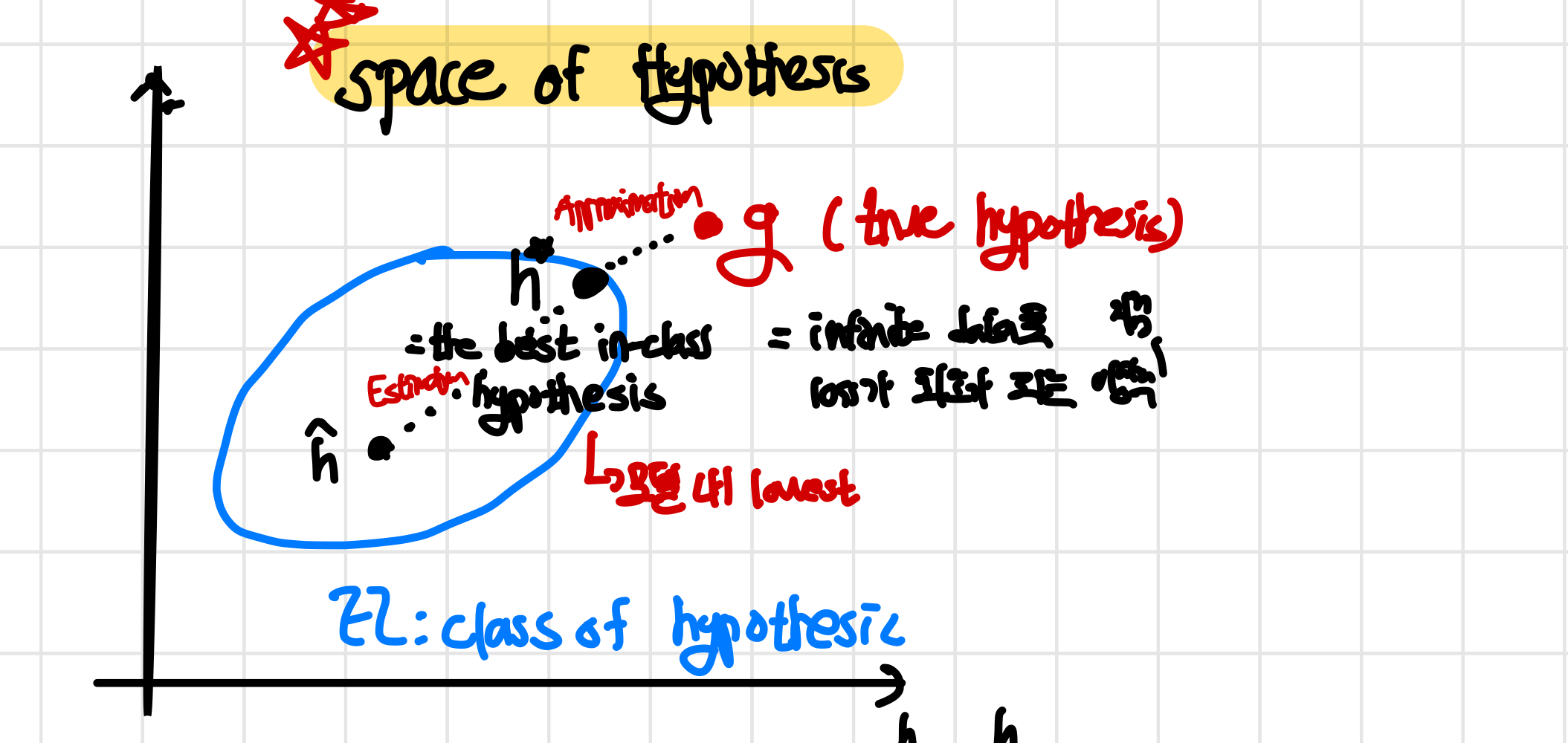
여기서는 hypothesis를 그래프 상에 배치시켜 hypothesis의 공간을 시각화해서 여러가지 개념들을 설명하게 된다. space of hypothesis를 나타내면 아래와 같은 그래프 같이 나타나게 된다. 참고로 이 것은 위에서 확인했던 parameter view의 더 일반화된 형태이다. (parameter θ에 대해서 나타낸 것이 아니라 parameter h에 대해서 나타낸거임!)

Error

이제부터는 여러가지 기호들과 error들에 대해서 알아보고자 한다! 위 사진의 space of hypothesis를 보면서 알아본다면 쉽게 이해 가능하다

<기호>

• g : best possible hypothesis (true hypothesis)
• $h^{\ast }$ : Best in class H 참고로 $h^{\ast }$가 어디인지는 알 수 없으며 hypothesis class에서 가장 최선의 값이다
• $\hat{h}$ : learnt from finite Data 흔히 우리가 training example을 통해 예측한 hypothesis이며 이 hypothesis가 $h^{\ast }$ 가 되기를 원한다
• ξ(h) : Generalization error (Risk= infinite process)generalization_error = $E(x,y)D[1(h(x)\ne y)]$ = E[make mistake] 즉, data generalization process중 distribution D에서 x,y를 sampling했을 때 예측값인 hypothesis가 실제값과 같은지에 대한 지표라고 보면 된다. 결국 예측이 실패할 확률, error가 날 확률이다
• $\hat{\xi }$ (h): Empirical error (Risk= finite process)empirical_error =$\frac{1}{m}\sum 1(h(x^i)\ne y^i)$ 실제 한정된 example을 input으로 넣어 hypothesis가 제대로 예측하는지에 대한 error를 나타낸다.

<error(에러)>

• ξ(g) : Bayes Error/ Irreducible Error best possible hypothesis가 error를 만들 확률! 아무리 best hypothesis라고 하더라도 0이 될 수는 없다 (error가 생길 수 밖에 없음 ex: x→ y1 값이 되기도 하고 x→y2 값이 되기도 할 때)
• $\xi (h^{\ast })-\xi (g)$ : Approximation Errorapproximation_error class내에서 최고의 hypothesis error에서 본래 최고의 error를 뺀 값으로 class내에 어떠한 hypothesis라도 최소한 이 error보다는 크다는데에 의미가 있다.
• $\xi (\hat{h})-\xi (h^{\ast })$ : Estimation Errorestimation_error empirical error에서 generalization error를 뺀 값으로 class 내의 hypothesis의 사실상 가능한 실제 성능에 대한 값을 의미한다

종합하자면 $\hat{h}$는 다음과 같이 표현이 가능하다. 그리고 이 generalization error를 여러 component로 나누어 보는 것이 여러 관점에서 이해하는데에 있어 중요하다. 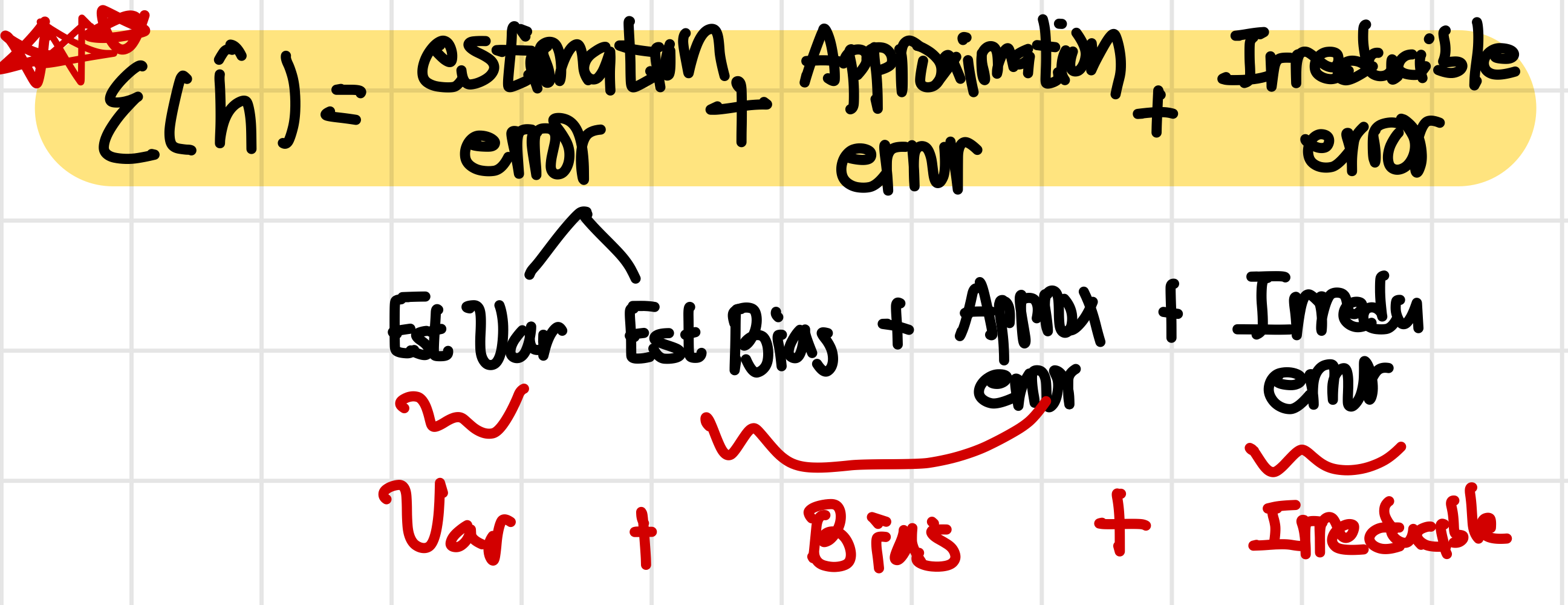error view: Irreducible error는 없앨 수 없는 값이고 Approximation error는 class를 정의하는 역할을 해서 알고리즘에 따라 달라지는 값이며 estimation error는 data의 제한된 정도와 알고리즘의 뉘양스에 따라 달라지는 값이다.

bias variance view: 이때 estimation error는 variance와 bias로 나눌 수가 있다. 그 이유는 어떠한 hypothesis를 선택하느냐에 따라 class 내에서 bias가 달라질 수 있으며 hypothesis class의 크기에 따라 variance가 바뀔 수 있기 때문이다!!

Approximation error는 결국 이상적인 g값과 얼마나 떨어져있느냐에 대한 문제이기 떄문에 bias와 관련이 있다. ($\hat{h}$는 class내에서 어쩔 수 없이 존재하게 되는 값이고 approximation error는 여기에서부터의 거리에만 관련이 있음, estimation error에서 이미 크기가 정해져 variance와는 관련이 적음)

CS229 8. Data Splits, Models & Cross-Validation 종합적으로 bias와 variance에 대해서 정리를 간단하게 하면!!!

bias는 $\hat{h}$가 g로 부터 왜 멀리 떨어져있는지를 생각해보면 된다. 즉 , hypothesis class가 너무 작아 approximation error가 큰 것이 영향을 미칠 수 있고 hypothesis내 data에 따라 estimation error가 증가한 것이 영향을 미쳤을 수 있다.

또한 variance는 대부분 data가 작아 hypothesis class가 커졌기 때문에 estimation error가 커져 증가했다고 보면 된다.

즉, generalization error를 통해 variance에 따른 효과(error)와 bias에 따른 효과(error)를 같이 합쳐서 생각해볼 수 있고, 왜 bias와 variance가 큰 것이 model에 나쁜지에 대한 설명이 가능하다는 점에서 의미가 있다

Empirical Risk Minimizer (ERM)

ERM 일종의 learning algorithm으로 모델을 학습시킬 때 사용되는 최적화문제에 나타내는 개념이다. 모든 learning algorithm중empirical_error 를 최소화 시키는 것을 목표로 하는 모든 algorithm을 말하며 이렇게 error를 줄이는 것을 목표로 할 때에 theorical result(어떻게 해야 error를 줄이고 error끼리 어떤 관계가 있는지 등)를 얻을 수 있다. 참고로 알고리즘이 무엇이든지 간에 위에서 언급한 bias-variance theory는 유지가 된다. 우리가 얻고자 하는 것은 hypothesis class내에 최적의 hypothesis $ϵ(\hat{h})$이며 이를 통해 estimation-approximation view 혹은 variance-bias view를 통해 모델 분석 및 error(loss)의 값을 추정할 수 있다 위에서 도식화한 것과 같지만 다른점은 learning algorithm이 ERM이라는 것과 그 결과로 나온 random variabe이 ${\hat{h}}_{ERM}$이라는 것이다. 그리고 ${\hat{h}}_{ERM}$은 다음과 같은 식으로 표현된다${\hat{h}}_{ERM}=arg{\max }_{h\in H}\frac{1}{m}{\sum }_i^{m}1\{h(x^i\ne y^i)\}$ 결국 ERM 알고리즘은 error를 최소화하여 accuracy를 높이려고 하며 logistic regression에서와 같이 maximize liklihood를 찾는다는 점에서 다르게 보일 수 있지만 결국 logistic loss를 줄여야하기 때문에 ERM에 근사가 가능하다

Tools

우리가 얻고자 하는 것은 hypothesis class내에 최적의 hypothesis $ϵ(\hat{h})$이며 이를 통해 estimation-approximation view 혹은 variance-bias view를 통해 모델 분석 및 error(loss)의 값을 추정할 수 있다

우리가 알고자 하는 것은 A) $\widehat{ϵ}$(training error)와 $ϵ(h)$ (generalizaiton error)와의 관계(training error을 줄이면 generalization error는 어떻게 되는지), 그리고 B) $ϵ(\hat{h})$ 와 $ϵ(h^{\ast })$ 와의 관계(learned hypotesis에서의 generalization error와 best possible hypothesis)이다. 이를 제대로 설명하기 위해서는 다음 2가지 이론을 알고 있어야한다!

Union Bound(합집합 부등식)

Union_bound 확률 이론에서 여러 사건의 확률의 합을 추정할 때 사용되는 부등식으로 어떠한 사건이 적어도 하나 발생할 확률을 추정하는데 사용된다. 참고로 각각의 확률 event들은 꼭 independent할 필요는 없으며 각각의 확률 event를 $A_1,A_2,\dots ,A_n$이라고 할 때 다음과 같은 부등식이 성립한다

$P(A_1\cup A_2\cup \dots \cup A_n)\le P(A{}_1)+P(A{}_2)+\dots +P(A_n)$

Hoeffding’s Inequality

Hoeffding_Inequality 큰 수의 법칙을 일반화한 결과로 표본평균(sample된 수들의 평균)이 기대값에서 멀리 떨어질 확률을 제한하는 부등식이다. 0과 1 둘 중 하나의 값을 갖는 $z_1,z_2,\dots ,z_m\sim Bern(ø)$이고 $\widehat{ø}=\frac{1}{m}{\sum }_i^m{z}_i$ 이며 $\gamma >0$(margin)일 때 다음과 같은 식을 만족한다.

$Pr[\stackrel{\text{maring r보다 큰 error에만 관심있음}}{\overbrace{\mid \underset{error}{\underbrace{\widehat{ø}-ø}}\mid >\underset{margin}{\underbrace{\gamma }}}}]\le 2\exp (-2{\gamma }^2\underset{\text{m이 커질수록 값 작아짐}}{\underbrace{m}})$

우측 항은 $\gamma$에 대한 식이고 자연스럽게 margin $\gamma$가 늘어나게 되면 이 margin보다 큰 error를 만들 확률은 줄어든다. 하지만 이것은 그렇게 되도록 식을 만든 것이고 어찌보면 당연하며 중요한 부분이 아니다. 중요한 것은 m으로 $\gamma$가 일정할 때 example의 수 m이 커져야만 error가 줄어든다는 것을 의미한다

ERM을 직관적으로 이해하기 위해 hypothesis(h)와 error($ϵ$)를 축으로 하여 generalization error와 empirical error를 표현하면 다음과 같이 나타낼 수 있다 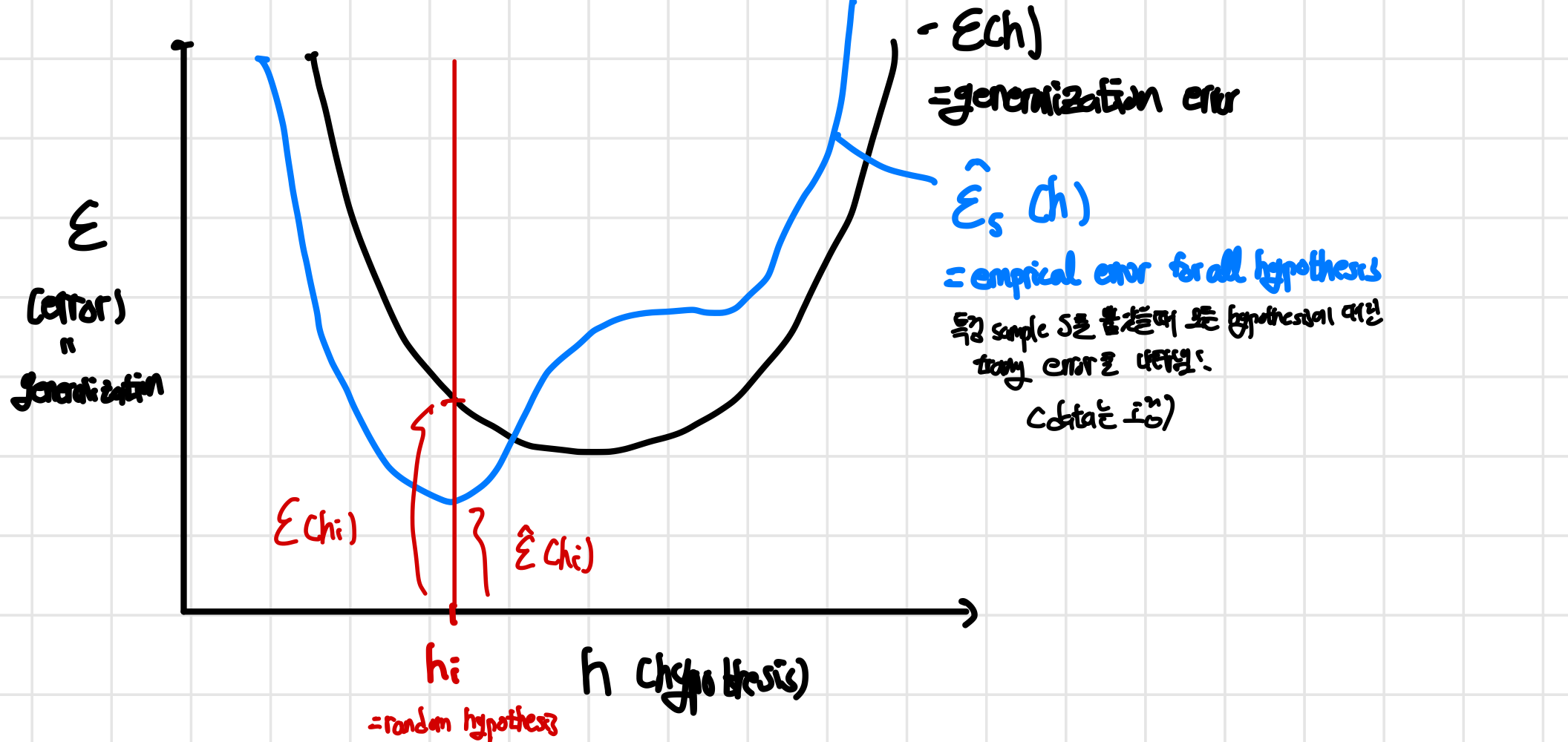각 error를 Hoeffding’s Inequality로 넣었을 때의 결과로 알 수 있는 것은 example의 수 m이 커질 수록 empirical error는 generalization error에 가까워진다는 것이며 위의 그림에서는 두 그래프가 인접해진다는 것이다. 사실 어떻게 보면 당연하게 generalization error은 모든 distribution의 값을 뽑았을 떄의 error이기 때문에 한번에 sample하는 개수가 많아지면 두 error는 가까워진다 Hoeffding’s Ineqaulity로 표현하면 다음과 같은 식이 나오게 된다

$Pr[\stackrel{\text{empirical과 generalization 관계}}{\overbrace{\mid \underset{\text{그래프 상에서 높이 차이}}{\underbrace{\widehat{ϵ}(h_i)-ϵ(h_i)}}\mid >\underset{margin}{\underbrace{\gamma }}}}]\le 2\exp (-2{\gamma }^2\underset{\text{m이 커질 수록 그래프 인접}}{\underbrace{m}})$

또한 수많은 S를 sample했을 때 그 S들의 empirical error의 평균은 generalization error와 같다. 이 뜻은 무한히 많은 empirical error 함수를 평균 냈을 때가 곧 generalization error와 같다는 것이고 Hoeffding’s inequality로 알 수 있는 것은 한번 sample할 때 많이 뽑게 된다면 두 error는 인접해진다는 것이다

$E[\widehat{ϵ(h_i)}]=ϵ(h)$

문제점: 하지만 지금까지 확인한 방법의 문제점은 random한 hypothesis에서 시작한 후 특정 sample S를 뽑았을 때 고정된 data의 평균을 계산했는데 실제로는 특정 data에서 시작해서 ERM을 통해 가장 error가 낮은 hypothesis h를 구해야한다!! 즉, 특정 empirical error 함수에서 가장 error가 낮게 만드는 hypothesis를 찾아야한다! (h random, S sample, Data 고정 → random Data , low h)

Uniform Convergence

Uniform_Convergence우리가 얻고자 하는 것은 hypothesis class내에 최적의 hypothesis $ϵ(\hat{h})$이며 이를 통해 estimation-approximation view 혹은 variance-bias view를 통해 모델 분석 및 error(loss)의 값을 추정할 수 있다

이러한 1) 문제점을 해결하고, 모든 h에 대해서 다룰 때(특정 h를 random하게 뽑아 확인X) bound가 어떻게 형성이 될 것인지와 2)이때에 어떻게 empirical risk curve(함수)가 일정하게(uniformly) generalization curve로 수렴(converge)하는지 알아보기 위해 Uniform Convegence에 대해 알아보자 한다.

1. 위에서 우리가 발견했던 문제점을 해결해야함
2. 1)에서의 문제점을 해결했을 때 위에서 우리가 Hoeffding Inequality로 얻은 결과가 새로운 방법에서도 적용이 되는지, 달리 설명하는지를 알아야함

여기에서 전에 언급했던 tool 2가지 중 첫번째, Union bound 성질을 사용할 수 있다. 즉, 모든 hypotheisis를 union한 것을 union bound에 적용하여 모든 h를 다룰 때도 bound를 얻을 수 있다는 뜻이다(1)이 가능하다! 그럼 어떻게?? )

Finite hypothesis class

hypothesis class의 크기가 finite(유한)할 때의 결과 자체가 크게 중요하지만 이것이 일종의 building block이 되어 infinite hypothesis class나 다른 결과를 유도할 떄 도움이 된다

Finite hypothesis class를 H라고 할 때 H의 크기(hypothesis의 개수와 유사) |H|를 k로 두고(|H|=k)Hoeffding_Inequality 를 적용하면 다음과 같은 식이 만들어진다

=&Pr[ \underbrace{ \forall h \in H }_{ \text{Union bound 이용!!!}}\mid \hat{\epsilon}(h_{i})-\epsilon(h_{i})\mid<\gamma]≥1-\underbrace{ 2k\exp(-2\gamma^2{ m }) }_{ \delta } \\ &\delta =2k\exp(-2\gamma^2{ m }) \text{ 라고 했을 때 이거에 대해서만 분석하면 됨} \end{align} $$ #Union_bound 를 이용하여 기존에 random한 h에서 시작한 것 대신에 모든 h에 대해서 Hoeffding Inequality를 사용할 수 있게 되어 이를 통해 모든 h에 대해서도 의미있는 결과를 도출할 수 있게 됐다(1&2). 참고로 어떤 h에서 모든 h로 바뀌면서 flip이 일어나 부등호의 방향이 바뀌게 되었다. 그리고 $\delta =2k\exp(-2\gamma^2{ m })$라고 했을 때 이에 대해서 분석만 하게 된다면 위의 식이 어떤 의미있는 결과를 도출할 수 있는지 알 수 있다. 그럼 알아보자!! - $\delta$ : probability of error (margin보다 큰 error들만 다룸) - $\gamma$ : margin of error - $m$ : sample size 여기서 2개의 변수를 고정시키고 나머지 하나를 알아보면 됨 **A) training error와 generalization error 비교** ($\hat{\epsilon}(h)$ vs $\epsilon(h)$) Fix $\gamma,\delta>0$ 했을 때 $m≥ \frac{1}{2r^2}\log \frac{2k}{\delta}$ ! 이 식을 만족시키면 (sample size m이 이것보다 크게 된다면)empirical error와 generalization error가 $\gamma$보다 작게 된다는 뜻이다! *sample complexity*: sample size m이 커지게 된다면 empirical error가 generalization error에 가까워진다는 것을 의미한다.(sample complexity는 sample size m이 정한다!) 즉, 1)에서의 문제점을 해결하면서 2)에서처럼 기존과 똑같은 결과를 얻을 수 있다!(똑같이 m이 커지면 generalizaton error에 가까워짐) **B) generalization error와 best possible error 비교** ($\epsilon(\hat{h})\text{ vs }\epsilon({h^*})$) 결국 generalization error을 알았을 때 이를 best possible error와 비교할 수록 식을 바꿔야한다. ![[Pasted image 20240307222331.png]] (1). 현재의 식은 empirical error 중 최소 error인 $\epsilon(\hat{h})$ 와 이때의 generalization error $\hat{\epsilon}(\hat{h})$ 사이의 관계만 알고있다. (Hoeffing Inequality에서 두 error가 margin보다 커야함) (2). 이를 empirical error curve(함수)에서 $\hat{h}$이 training set에서 가장 작기 때문에 ($\hat{\epsilon}(\hat{h})<\hat{\epsilon}(h^*)$) 부등식을 바꿀 수 있다. (3) 여기서도 margin $\gamma$ 보다 커야하기 때문에 새로운 부등식을 만들 수 있다. 이를 통해 empirical error간의 관계에 대해서 알 수 있고 이를 hypothesis-error 그래프 상에서 표현하면 다음과 같이 나타낼 수 있다! 결국 Hoeffing Inequality에서 처럼 $1-\delta$ 의 확률과 training size m을 통해 $\hat{h}$의 generalization error와 관련된 bound를 표현하면 다음과 같이 식을 쓸 수 있다. $$\epsilon(\hat{h})≤\epsilon(h^*)+2\sqrt{ \frac{1}{2m}+\log \frac{2k}{\delta} }$$ ![[Pasted image 20240307222607.png]] *즉, 알고리즘이 ERM(loss를 최소화하는게 목적)이라면 sample size만 바꾸더라도 error가 바뀌게 된다!!* (training error를 줄이고자 한다면 sample size만 바꾸면 됨) ### Infinite hypothesis class hypothesis class의 크기가 무한한 경우에 $\hat{h}$의 generalization의 bound를 정할 때는 VC dimension을 사용해야한다. 이때 #VC_dimension 은 infinite size를 평가하는 지표로, 모델이 얼마나 복잡한 패턴을 표현하고 복잡한 패턴을 학습할 수 있을지를 측정하는 지표이다. 즉, VC(H)= some number이 된다. $$\epsilon(\hat{h})≤\epsilon(h^*)+O\left( \sqrt{ \frac{VC(H)}{m} \log\left( \frac{m}{VC(H)}+\frac{1}{m}\log\left( \frac{1}{\delta} \right) \right)} \right)$$ 즉, infinite hypothesis class는 VC dimension에 의해 sample complexity가 정해지며 이를 통해 $\hat{h}$의 generalization bound를 한정시킬 수 있다. *우리가 얻고자 하는 것은 hypothesis class내에 최적의 hypothesis $\epsilon(\hat{h})$이며 이를 통해 estimation-approximation view 혹은 variance-bias view를 통해 모델 분석 및 error(loss)의 값을 추정할 수 있다. 즉 Uniform Convergence를 통해 $\epsilon(\hat{h})$를 구할 수 있다!*