🪴 Quartz 4.0

Search

SearchSearch

CS231n 6-1. Setting Up Architecture (Activation Functions)

Dec 22, 202415 min read

Question

지금까지는 classifier와 neural network가 어떤 것인지 배웠다면 이제부터는 이 neural network를 지금까지 배운 구조, 학습 방법들을 통해 어떻게 학습을 할 것인지 알아보고자 한다. 그러기 위해 앞으로 neural network를 만드는 방법(구조를 어떻게 짤 것인지), 학습 방법들(어떻게 parameter와 hyperparameter을 정할 것인지), 이렇게 만든 모델을 어떻게 평가할 것인지 알아볼 것이다.

먼저 여기서는 activation function에 대해서 알아보고자 한다!

activation function에서 문제가 되는 특징이 크게 2가지가 있는데, 이 2가지를 토대로 activation function들이 어떤 특성을 가지고 있는지 확인하고자 한다

  1. 역전파 소멸 문제 (gradient kill 혹은 dead neuron)
  2. activation function의 값들이 0을 중심으로 분포되어 있지 않는 문제

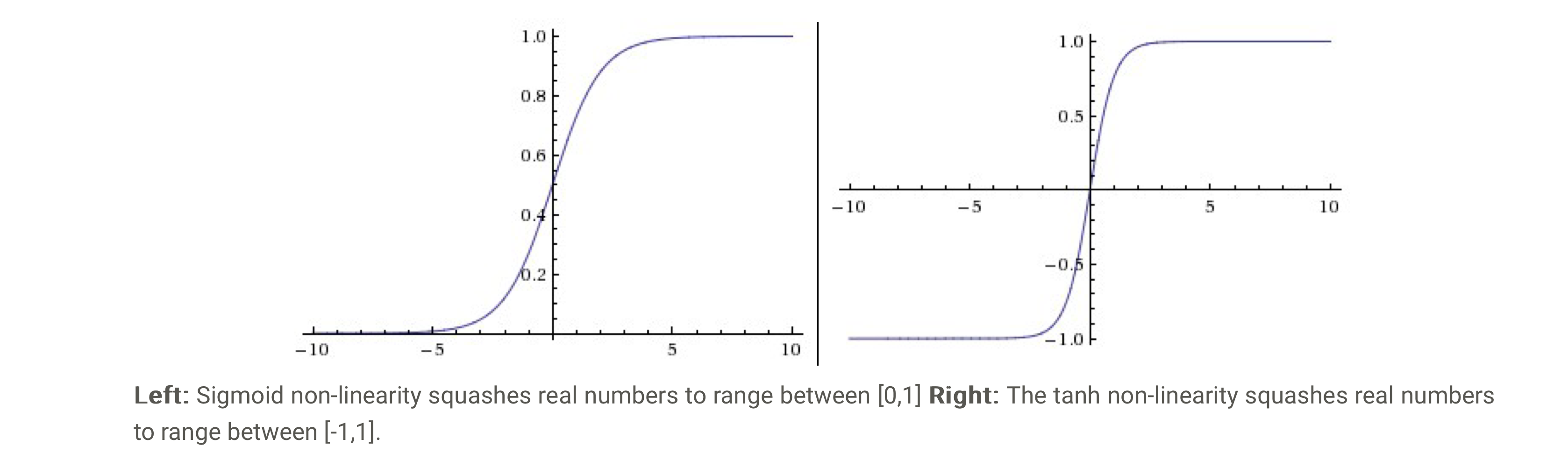
Sigmoid (1X 2X)

sigmoid : 함수값이 항상 양수이며 0~1 사이로 치역을 만들며 neuron이 얼마나 fire됐는지의 비율을 보여준다고 생각하면 된다. neuron이 아예 firing(반응)하지 않으면 0, neuron이 완전히 반응할 경우(fullysaturate) 1의 값을 낸다. 다만 sigmoid는 매우 초창기에 쓰였던 activation function으로 다음과 같은 이유들 때문에 현재는 거의 사용하고 있지 않다

단점

  1. kill gradient: input value(x)가 ∞나 -∞로 수렴할 경우(즉, 뉴런이 saturate될 경우) gradient가 0에 수렴하게 된다
    • backpropagation 에서 local gradient(almost zero) X upstream gradient로 계산이 되므로 이므로 local gradient가 0에 수렴하게 되면, 이 노드부터 아래에 있는 모든 노드들은 gradient가 0이 되는 문제를 가지게 된다
    • 또한 sigmod의 도함수의 최대값이 0.25이기 때문에 여러번 지나가면 값이 매우 작아짐
    • 이게 recursively하게 적용되어 모든 gradient의 값들이 kill되는 문제점을 가짐 weight initialization이 큰 값으로 될 경우 값들이 매우 커져 결국 포화되는 경우가 많음
  • [!] initalization에 대해서는 후에 더 자세하게 다루니 알고 있으면 됨
  1. Not zero centered: 식과 그래프에서 알 수 있듯이 이 함수는 원점에 대해 대칭이 아닌데 이것이 문제가 된다.
    • sigmoid의 함수값이 항상 양수이기 때문에 에 대한 local gradient 가 에 대한 식으로 나타나지고 이 값이 항상 양수가 된다
      • gradient= local gradient X upstream gradient인데 local gradient의 부호가 항상 양수이므로 최초의 upstream gradient에 따라 항상 부호가 양수이거나 음수로 결정
    • zig-zagging 일관된 방향으로 수렴하지 못하는 현상으로 parameter 가 갈 수 있는 방향에 제약이 생긴다
      • 가중치가 update될 수 있는 방향이 정해지며 밑에 그림에서 w가 갈 수 있는 원점에서부터 시작되는 vector들의 합으로만 실제 최적의 w vector를 표현이 가능하다.
      • 항상 치우친 출력을 거쳐(양수/음수) 가중치 업데이트가 되어 일관된 방향(결과값)으로 쉽게 가지 못함
  2. 지수함수의 연산: Sigmoid는 exp함수가 존재하는데 이 연산이 연산적으로 복잡한 편이지만 실제 내적연산이 더 복잡한 편이기 때문에 그렇게 큰 문제가 되지는 않는다.

그렇기 때문에 평균이 0인 (zero-mean) activation function을 도입하여 이러한 문제를 해결하고 Tanh 함수가 나오게 되었다.

Tanh (1X 2O)

Tanh 함수의 값을 -1~1 사이로 만드는 함수로 Sigmoid의 2) zero-centered하지 않는 특성을 보완했지만, 여전히 1) gradient가 죽는 특성이 있다. 결국 이 함수는 zero-centered하기 때문에 항상 Sigmoid 보다 선호되지만 여전히 역전파 중에 gradient가 소멸되는 현상을 해결하지는 못한다

ReLU (1O 2X)

ReLU: Recified Linear Unit의 줄임말로 요즘들어 가장 많이 쓰이는 함수 중 하나로, 특히 실제 뉴런의 동작과 비슷하다는 특징이 있다. gradient killing문제를 반만 해결하고 zero-centered하지 못하다는 단점이 존재하지만, 연산이 빨라 쉽게 학습이 가능하며 gradient killing 문제를 반은 해결하여 자주 사용되는 함수이다.

장점

  1. Accelerate Convergence & Cheap Operation

    • gradient descet 과정에서 x가 0이하면 0, 0이상이면 1로 gradient를 구하기 매우 쉽고 빠르다.
    • 앞에서 본 함수들은 지수함수이기 때문에 연산 비용이 비싸지만, ReLU는 일차함수로 이루어진 non-linearity 함수이기 때문에 연산에 매우 효과적이다.

  2. Not be Saturated

    • x(input) 값이 무한대로 갈 때 gradient값은 0이되지 않아 neruon이 포화되지 않는다. 다만 saturated되지 않을 뿐 gradient vanishing(dying neuron 문제는 생길 수 있다.

  3. Sparse Network

    • input이 음수일 경우에 값이 0이 되기 때문에 weight가 sparsity 해지는 효과를 얻어 실제로 문서의 의미있는 부분을 처리할 가능성이 높아져 과적합의 가능성을 줄이고 효율성을 증가시킨다
    • 예를 들어, 사람의 얼굴을 감지하는 모델이 있을 때 얼굴 사진이 input일 때 귀를 식별하는 뉴런이 활성화되는 반면(1) 산을 식별하는 뉴런은 아예 활성화가 되지 않어(0) 효과적으로 구분 가능!

단점

  1. Dying Problem
    • 입력이 음수일 때 출력이 0이되어 다시 activate되지 못하는 문제가 생기며, 이로 인해 back pass에서 local gradient의 값이 0이 되어 사라지면 다시 살아나지 못하는 gradient vanshing(dying neuron) 문제가 생긴다
    • initalization과정에서 초기의 bias를 0.01로 잡아 시작하자마자 죽지 않도록 만들거나, learning rate를 줄이는 것이 해결책 중 하나이다.
    • 실제 구현해서 10~20% 정도 dead neuron들이 발견되지만 이 정도는 실제 성능에 크게 영향을 주지 않는다고 하다 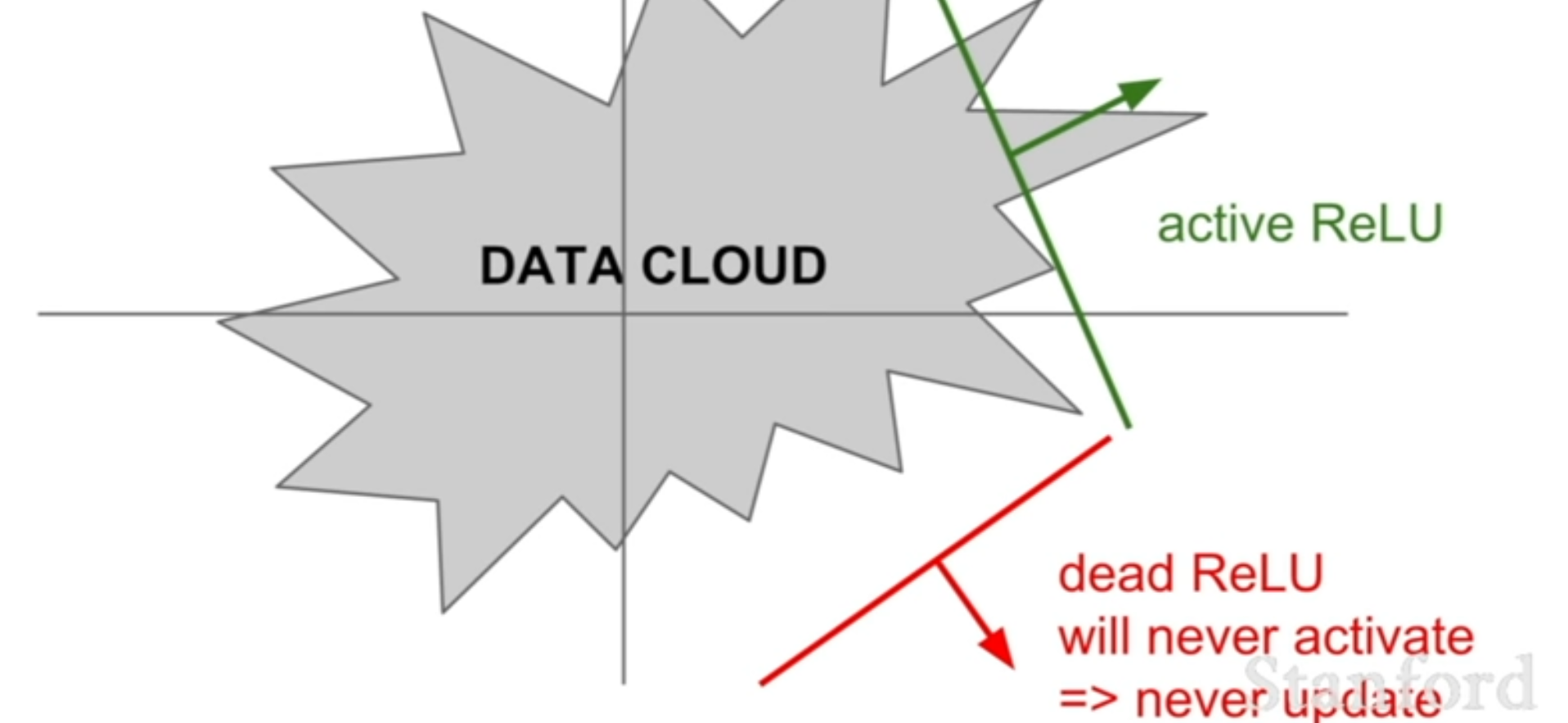위 사진에서 data cloud란 training data를 의미하며 ReLU가 이 data cloud 내에 존재해야만(x>0) 유의미한 값을 의미하여 죽지 않는 반면에 이외에 존재할 경우 activate하는 경우가 없기 때문에 절대로 update되지가 않아 죽는문제가 생긴다.

즉, input data와 관련이 없는 부분으로 weigth가 초기화될 경우 처음부터 neruon이 죽을 수 있으며, 높은 learning rate는 neuron이 데이터가 들어가있는 부분에서 벗어나게 만들어 빠르게 음수인 구간으로 빠지게 만들 수 있다

  1. Accumulate Large Error(Exploding)

    • 큰 오류 gradient가 누적되어 가중치(weight)가 매우 크게 업데이트 되기도 함
    • 상대적으로 gradient의 크기가 큰 편(0혹은 1)

  2. Not zero-centered

Saturate VS Dying

  • Saturate: Activation function의 x가 ∞나 -∞로 갈 때 도함수(gradient)가 0 혹은 매우 작아져 기울기가 거의 변하지 않는 상태이다. 즉, 너무 값이 커져서 그러는 것이 아니라 gradient가 작아져서 생기는 문제
  • Dying: ReLu함수에서 입력이 음수일때 출력이 0이 되어 뉴런이 죽어버는 상태이며 즉, back pass에서 local gradient=이므로 x에 대한 식에서 x는 0이 되어 gradient가 전파되지 않고 업데이트 되지않는 상태이다.

⇒ReLU는 saturate(X), dying(O),killing(X) Sigmoid는 saturate(O), dying(X), killing(O) 이며 미묘하게 각 함수의 상태를 나타내는 용어가 다르다는 것을 유념해야한다.

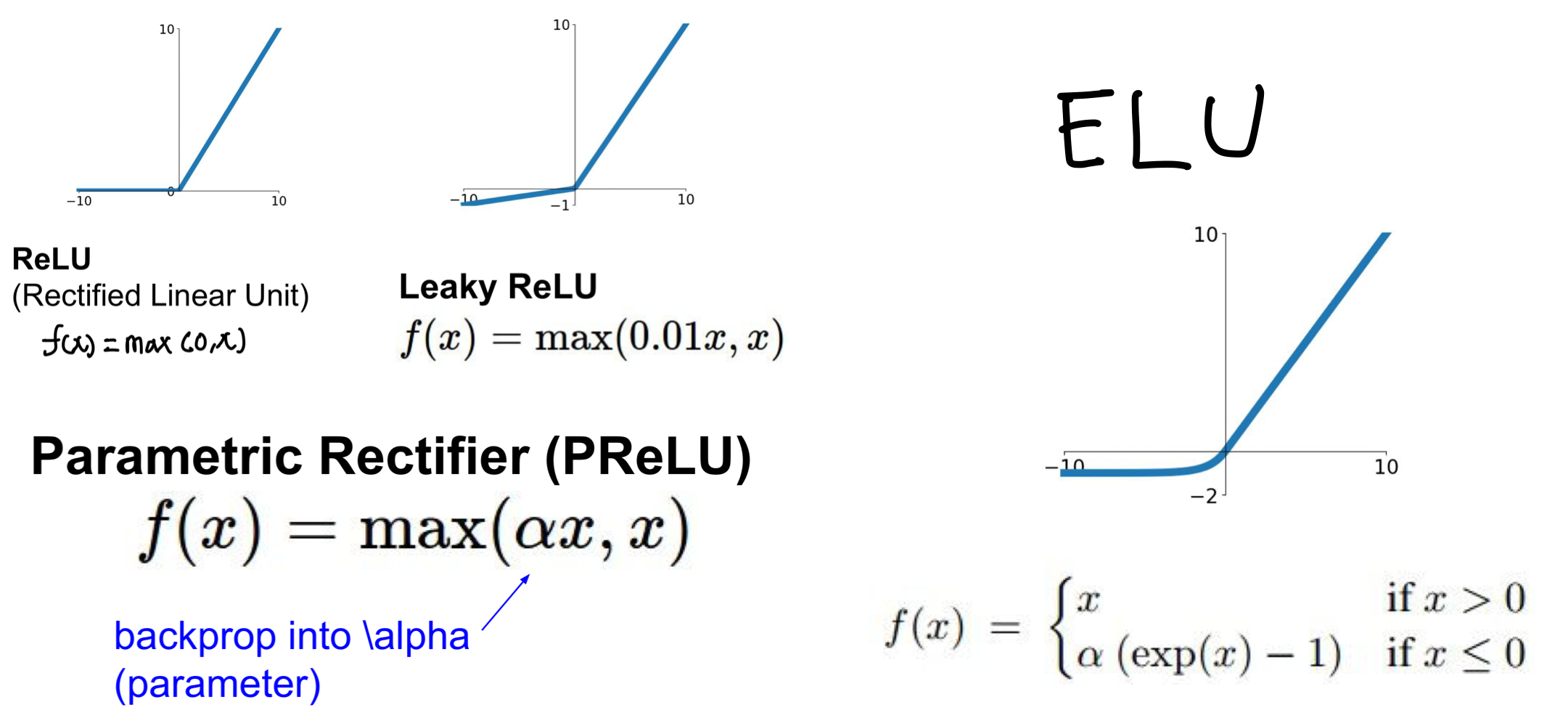
Leaky ReLU

ReLU의 단점 1) Dying problem을 해결하기 위한 방법으로 고안이 되었으며 x의 값이 0보다 작을 때 함수를 사용하여 함수 꼴을 가진다. ReLU의 장점은 가지면서(연산과 학습에 유리) input x가 0보다 작을때 neuron이 dying하는 문제를 해결한다.

PReLU

꼴을 가지며, Parameteric ReLU 라는이름에서도 알 수 있다 싶이 도 하나의 parameter로 보아 훈련중에 작은 값으로 학습가능하다는 flexibility를 가지고 있는 것이 특징이다. parameter에 더 잘 적응할 수 있도록 input이 0보다 작은 값일 때 사용자가 알맞는 값을 찾을 수 있다.

ELU

ELU Expotential Linear Unit의 약자로 이름에서 알 수 있다싶이 0보다 작은 input에 대하여 linear 함수를 사용하는 것이 아니라 지수함수를 사용하여 LeRU의 문제점인 2.exploding과 3. not zero-centered를 해결한다. ReLU와 Leaky ReLU 사이에 형태를 띈다. 3) 이 함수로 인해 함수의 평균이 0으로 이동됨 2) 음수값 포화상태(negative saturation regime)가 존재하지만 오히려 이 포화영역이 noise에 강건성(robutness)를 높이는 역할을 한다.

단, 지수함수라 계산속도가 느리지만 함수의 평균이 0이되어 zero-centered의 효과로 빠르게 최적의 값으로 수렴된다고 주장

포화영역(saturate)이 좋을 수도 있는가?

위에서 보았던 ReLU에 경우 음수 입력에서 완전히 0이 되어 neuron이 죽은 상태가 되지만 ELU는 부드럽게 포화되도록 만들어 nueron이 죽는 상태를 막으면서도 gradient가 0이 되는 현상을 최소화한다.

이에 더해 ELU의 음수부분은 학습 중에 약간의 노이즈가 포함이 되더라도 출력에는 큰 영향을 미치지 않아 안정적인 출력을 제공한다. 즉, ReLU의 neuron이 죽는 현상을 없애는 동시에 포화됨으로써 나타날 수 있는 문제점을 최소화하고 오히려 새로운 장점을 제시하게 된다

Maxout (1O, ReLU 결점보완)

Maxout 여러개의 linear function을 조합하는 형태로 이 중 최댓값을 계산하여 하나의 function을 만든다. 즉, ReLU와 Leaky ReLU 등의 일반화된 형태로 만약 k=2로, 하나의 함수는 0, 하나의 함수를 x로 둘 경우 ReLU와 같은 형태가 된다.

또한 결국 선형 함수들의 최대값을 취하기 때문에 비선형성을 유지하면서 기울기가 0이 되는 문제를 없앨 수 있다. 이때 k만 정하면 사용되는 선형함수들은 모델이 학습과정에서 역전파를 통해 최적화하여 자동으로 학습하게 된다.

ReLU의 모든 장점을 가지면서 gradient가 saturate 되거나 neuron이 죽는 단점을 가지지 않으며 단점이라 하자면 function의 배수 만큼 parameter의 수가 증가하게 되고 gradient의 계산이 복잡해지며, 결국 를 최적화해야하므로 모델의 학습 시간이 더 걸릴 수 있다.

Conclusion

  • learning rate에 신경을 쓰며 ReLU를 사용하는 것이 좋다!
  • Leaky ReLU , Maxout , ELU를 한번쯤 시도해보는 것이 좋다
  • tanh를 시도해보는 것은 좋지만 크게 기대하지 않는 것이 좋다
  • sigmoid 는 쓰지마!

Graph View

Backlinks