Summary

score의 값이 실제 값과 얼마나 차이나는지 확인하고, 실제 값과 유사하게 만들기 위해 나온 함수가 loss function이다. 이 Loss function에는 정답인 class와 그렇지 않는 class의 score의 차이와 margin을 비교하여 loss를 만들어내는 SVM 함수와 score 자체를 의미부여하여 cross entropy loss를 이용해 확률적으로 해석을 한 Softmax 함수가 존재한다.

Loss Function

score이 실제 값과 얼마나 차이나는지 확인하고 현재 classifier가 얼마나 좋은지 확인하기 위해서 새로운 function이 필요하게 되었고 그것이 바로 loss function이 되었다. 즉, W가 얼마나 좋은지(얼마나 분류를 잘하는지)를 확인하는 척도가 된다. 만약 loss가 높다면, 이는 training data를 분류하는데 잘못하고 있다는 것이다.

현재까지는 Linear Classification에서 score을 어떻게 내는지 확인했지만 이 스코어가 얼마나 좋은것인지, 이에따른 classifier가 얼마나 좋은 것인지, 우리가 조절할 수 있는 parameter인 W,b를 어떤 수로 넣을지를 배우지 않아 이것을 Loss function을 통해 알아보고자 한다.

1. Multiclass SVM loss (Support Vector Machine)

CS229 6. Support vector machine (SVM)에서는 binary class에 대한 경우를 주로 다루는데 이를 현재 이 강의에서 다루고 있는 10가지 이상의 class에 대해 적용하기 위해서는 일반화가 필요하다. 간단하게 SVM의 개념을 얘기하자면, 어떤 margin $\nabla$ 에 대해서 정답인 class score가 정답이 아닌 그 어떤 class의 class score에 margin을 더한 값보다 커야만 loss가 0으로 간주하며, 그렇지 않은 값들은 모두 합하여 SVM loss가 나오게 된다.

$s_{j} = f (x_{i}, W)$ :즉 $s_{j}$ 는 input x에 대해 j번째 class의 score을 의미
다른 class의 score값이 정답인 class의 score값보다 높게 측정한다면, 이는 parameter W가 잘못되어있고 update되어야 할 여지가 있다는 것을 의미하며 이를 loss로 penalty를 줘서 update할 수 있도록 만들어준다.
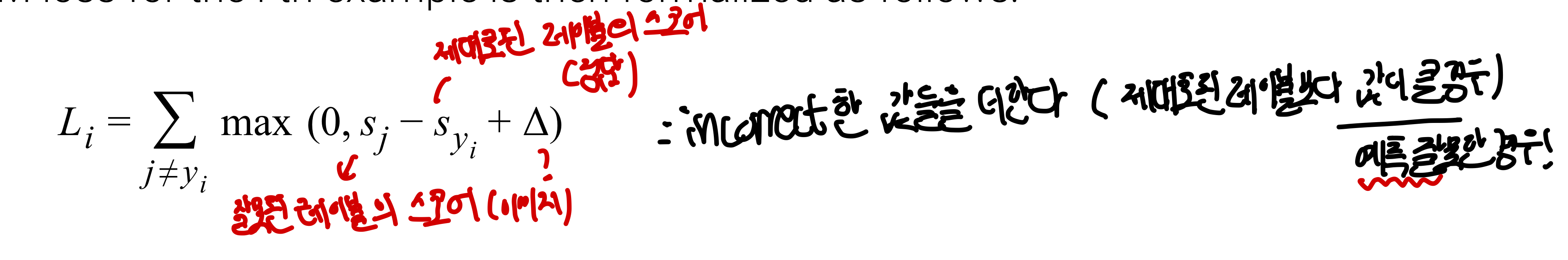
그렇다면 어떤 기준으로 loss를 줘야할까?? ➡️맞은 class에는 높은 점수를 주고(loss를 안줌), loss는 줄이는 것이 목표 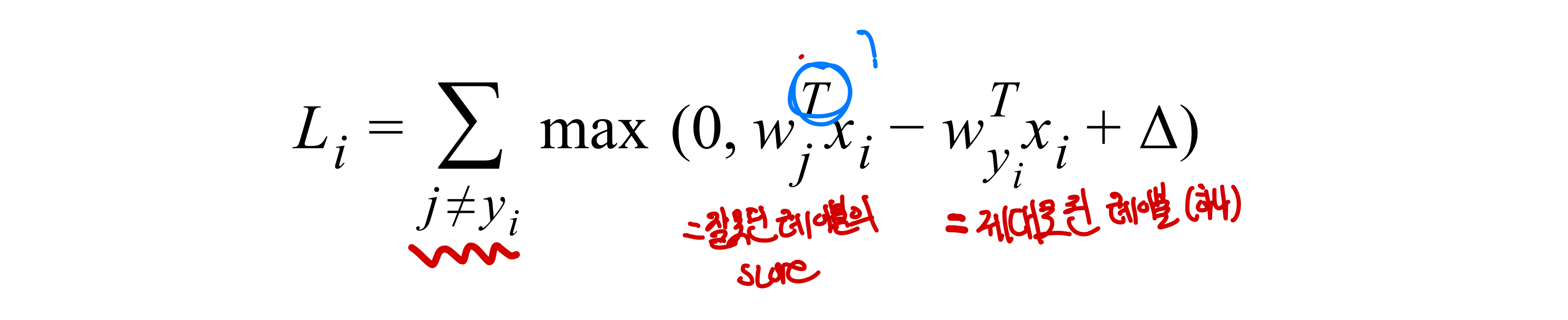즉, $s_{j}$ (다른 class의 score)+ $\nabla$ < $s_{y_{i}}$ (맞는 class의 score) 이어야 Loss가 생기지 않음
$S_{j}$ : 잘못된(정답이 아닌) class의 score
$S_{y_{i}}$ : 정답인 레이블의 스코어값
$\nabla$ : margin, $L_{i}$ : loss의 총합 (두 사진은 똑같은 식인 것을 나타내고 있음)

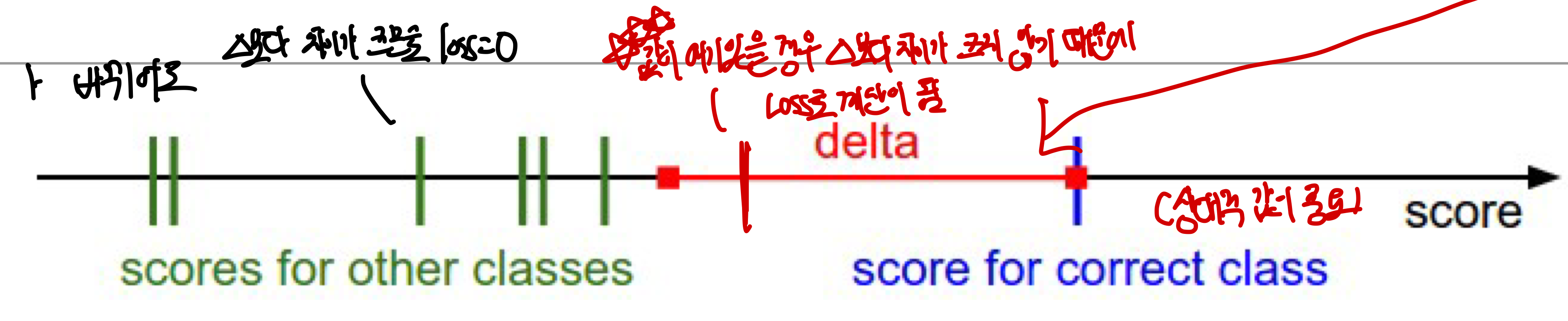
SVM loss의 종류

hinge_loss: 맞는 class의 score값이 특정값 이상이면 loss가 0, 특정값 이하면 직선의 방정식(linear)에 따라 loss가 결정되는 함수로 주로 $ma x (0, f (x))$ 꼴에 함수에서 나타남
squared hinge loss SVM(L2-SVM): $ma x (0, f (x))$ 값에 제곱을 한 경우로 margin(차이)에 더 많은 penalize할때 주로 사용이 되며 기존의 SVM loss와는 다른 loss function이 되기 때문에 상황에 따라서 다르게 사용할 수 있다. (특히 매우 안좋은 경우를 심하게 싫어해야할 때 사용)

SVM loss의 특징 및 한계점

loss의 절대적 값이 중요하지 않음! == loss로 나온 숫자들이 무슨 의미를 가지고 있지 않음
- 상대적 값이 중요하며 상대적인 비교가 중요하기 때문에 🔺(델타)의 값이 큰 영향을 주지는 않음
- 주로 arbitary한 choice를 하게 됨
만약 아래 그림처럼 car 점수가 다른 값에 비해 score이 높을 때 이 score가 바뀌어도 loss에는 영향 없음
학습 초기에 W의 값이 매우 작게 초기화되어 score가 0에 가깝게 모두 나온다면 loss의 값은 $\nabla$ 이 된다.(score가 0이 될거고, 델타만큼은 커야함) 즉, $s_{j} = W X x$ 인데 이때 W가 0에 가까우면 score가 0이 됨 ➡️ 디버깅 전력으로 사용이 되는데 처음에 loss가 $\nabla$ 가 나오지 않는다면 loss를 잘못계산하고 있다는 말이 되기 떄문이다.
최솟값은 0이며 최대값은 무한대

Loss가 0인 weight W가 있다고 한다면, 이러한 W는 무수히 많아서 어떤 W가 가장 좋은지 알 수 없게 되는 문제가 생기게 된다. (만약 W의 크기를 n배 증가한다고 하면 score 사이의 간격도 n배 증가하여 Loss는 계속해서 0이 된다)

➡️ 오직 train data에 대해서 나온 값들에 의해 loss가 정해지므로 classifier가 어떤 W를 사용해야하는지 알 수 없다. 실제로 중요한건 test data에서 실제로 잘 동작을 하는지이다!

➡️ regularization을 이용하여 모델이 더 간단한 W를 뽑게 만들어 overfitting이 되지 않게 만들고 새로운 데이터가 왔을 때 제대로 된 분류를 하게 만듦(Occam's Razor-simplest is the best). train data로만 학습할 경우 overfitting 문제가 생기게 된다. (2차원 그래프에서 생각해볼 경우 각 data point들이 연결된 매우 구불구불한 선이 생기게 되어 실제 test에서는 효과를 얻지 못함)

Multiclass SVM loss동작과정

이 예시에서는 margin=1로 잡고 있다!

$x_{1}$ , 고양이의 경우: $s_{y_{c a t}} = 3.2$ 인 것을 알 수 있는데 loss가 없기 위해서는 다른 모든 class의 값들이 2.2이하여야 한다. 하지만 car의 점수 5.1점이기 떄문에 loss가 발생하고 loss를 구해보면 $L_{1} = 5.1 - 3.2 + 1 = 2.9$ 임을 알 수 있다.
$x_{2}$ 자동차의 경우: $s_{y_{c a r}} = 4.9$ 이므로 loss가 없기 위해서는 다른 모든 class의 값이 3.9이하여야하는데 실제 이 값보다 적으므로 loss=0이 된다
$x_{3}$ 개구리의 경우: $s_{y_{f ro g}} = - 3.1$ 이므로 loss가 없기 위해서는 다른 모든 class의 값이 -4.1 이하여야 한다. 하지만 실제로 그렇지 않으므로 loss를 구해보면 $L_{3} = (2.2 - (- 3.1) + 1) + (2.5 - (- 3.1) + 1) = 12.9$
전체 Loss $L$ : 결국 구해지는 전체 loss는 각 데이터 $x$ 에서의 loss들의 평균이므로 $L = \frac{2.9 + 0 + 12.9}{3} = 5.27$

그럼 이 margin $\nabla$ 는 어떻게 정할까?

$\nabla$ 의 값이 얼마로 잡아야 좋을지는 확실하게 알 수 없으며 무작위한 선택으로 할수 밖에 없다! 다만 여기서 score의 절대적인 값이 중요한 것이 아니라 상대적인 차이가 중요한데 weight값이 rescaling됨에 따라 margin이 무시되기도 함으로 크게 중요하지는 않다고 얘기한다. 다만 어느정도의 margin이 존재해야만 일반화에 유리하다고 한다

2. Softmax classifier

Score 자체에 의미가 있는!! classifier라는 점에서 multiclass SVM과 차이가 있다. CS229 4. Generalized Linear Model (GLM) (Softmax ) 여기에서 자세하게 그 방법을 다루며 주로 deep learning에서 더 주요하게 다룬다. 특징으로는 주어진 입력에 대한 각 class score을 계산하고 이 점수들을 확률로 변환한다는 것이다.

SVM과의 차이점 및 특징

function mapping $W X x_{i}$ (실제 연산)에는 아무런 차이가 없지만 score가 이제는 각 class에 대해 확률값으로 정규화되지 않는 확률을 나타내는 log값이 된다. 즉, score 값이 특정 범위 이상이거나 이하일 때 의미 있었던 SVM과는 달리 그 값 자체로 의미가 생기게 됐다.
loss 역시hinge_loss 에서cross-entropy_loss 로 바뀌었으며 이때entropy 란 데이터의 불확실성을 정량화하는데 사용이 되며 1) 확률이 한 곳에 집중되어 있으면 불확실성이 없기 떄문에 0이라고 볼 수 있고 2) 모든 class가 동등한 확률을 가질 경우에는 정보가 너무 다양하게 되어 예측이 어렵고 데이터가 불확실하며 엄청나게 많은 정보들을 추가적으로 얻어야만 분류를 한다는 것을 의미해 entropy가 최대값을 가진다.
Classification에서 자주 사용되는 방법으로 smooth하게 loss가 변하지 않아 SGD에서는 사용불가능함6. Binary Classification(cross-entropy-loss는 probability 분포 사이의 거리를 구해 이 거리를 최소화하는 것을 목표로 하며 잘못된 probability prediction에 대해서 penalize한다)
출력함수를 정규화된 class 확률로 해석!!(cross-entropy loss를 이용)

SVM 동작 방식!

스코어 자체를 loss로 쓰는 것이 아닌 지수화를 시킴 (각 점수를 양수로 만듦) score: unnormalized log probability => unnormailized probability ➡️주어진 데이터에 대한 상대적인 확률을 log라는 이름을 이용해 표현한 거임!
정규화 진행 : 모든 점수의 합으로 각 점수를 나누어 정규화시키고 이를 통해 class score을 확률로 나타낸다unnormalized probability => normalized probability
-log를 씌움: 이를 통해 cross-entrophy-loss를 구하게 되며 범위가 0~~1에서 0~~ $\infty$ 로 바뀐다. 이때 -를 추가한 이유는 2) 정규화 단계에서는 정답 class의 score 비중이 높을 때(정답이 확률이 높을 때) softmax function 값이 커지지만, loss는 정답에 가까울 수록 줄어야하기 때문이다.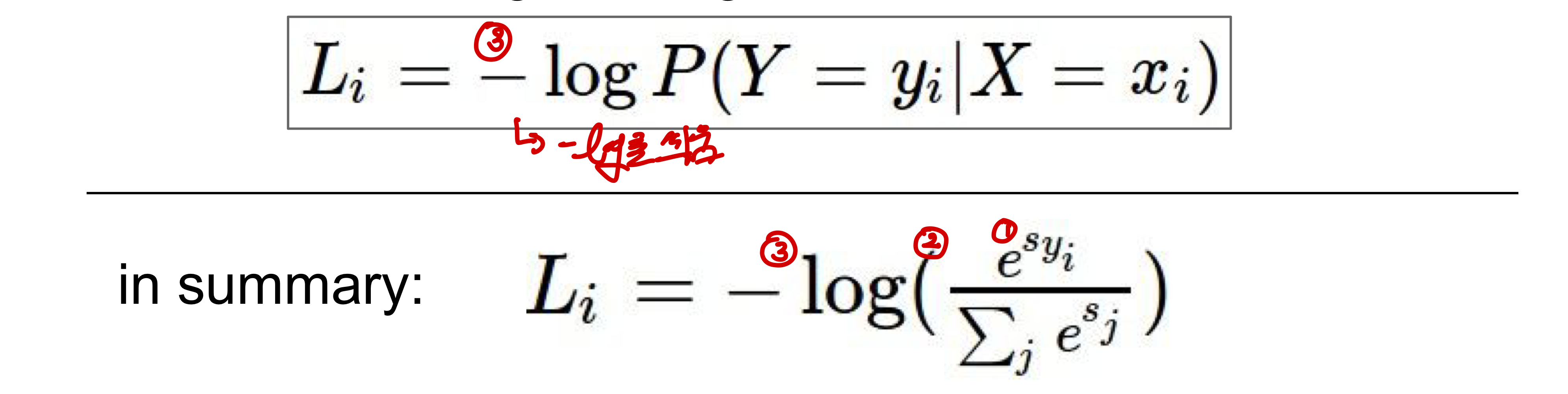

실제 구현을 할 때 조심해야할 점

softmax의 최솟값:softmax의 최대값은 ∞, 최소값은 0이 되는데 이때 실제 구현을 할 떄 최소값이 0이 되기 위해서는 정답인 class는 ∞의 score을, 나머지 class에 대해서는 -∞를 가져야하므로 실제 학습이 이와 같이 되기 어려울 뿐만 아니라 컴퓨터 역시 계산이 쉽지 않아 0이 나오는 경우는 거의 없다.

W 초기화했을 때los때는 $lo g (C)$ : 맨 처음 W를 초기화할 때 주로 W의 값이 작아 대부분의 score가 0에 가깝게 측정이된다. 그렇기 때문에 이를 지수화한다고 하더라도 모든 값이 1이기 떄문에 이를 normalize하여 loss를 내며 loss= $lo g (C)$ (C는 class의 개수)가 되며 이를 통해 debugging을 해본면 된다

정보이론적 관점(Information theory view)에서 바라본 Softmax

#cross-entropy_loss 최소: 하나의 image에 대해 1) 각class마다 계산한 정답 확률(q)과 2) 실제 class 분포(p) 사이의 확률 분포를 최소화하는 것을 목표로 하는 loss라고 보면 된다.entropy

사진에서의 q를 의미: 모델을 통해 나온 결과값
올바른 class에 모든 확률 질량이 분포(정답인 곳만 값이 1!!) p 백터는 $y_{ㅑ}$ 즉, i번째 위치(정답인 사진의 위치)에 1이 있고 나머지는 0이 백터로 실제 class에 모든 확률 질량을 두는 분포와 예측 확률 사이의 차이를 줄이는 것을 목표로 한다

이는 KL divergence를 이용한 식으로 표현이 가능하며 $H (p, q) = H (p) + D_{K} L (p ∣∣ q)$ 로 표현이 가능하다. 사실상 H(p)는 0(분포에서 1이 단 하나)이기 때문에 이 값은 곧 p와 q 사이의 distribution의 차이라고 볼 수 있으며 결국 cross-entrophy loss를 줄이는 것은 p와 q 두 distribution의 차이를 줄이면 것이라고 생각하면 된다. (KL을 이용한 엔트로피 해석 방법)

확률적 해석(Probabilistic interpretation)에서 바라본 Softmax

Softmax function의 결과를르 주어진 입력에 대한 각 class의 정규화된 확률로 해석하며 강의에서 그리고 위에서 언급했다 싶이 결국 correct class에 대해 negative log 값이 최소화되는 것을 목표로 한다는 관점이다.

즉, 이는 MLE(Maximum Likelihood Estimation)MLE 라고 볼 수 있으며 x에서 y를 뽑을 분포(distribution)을 W로 표현한 것이라고 볼 수 있다. 오른쪽항에 있는 식이 곧, input x들의 분포에서 정답인 y class를 sample하는 확률을 나타낸다고 보면 된다 CS231n 14. Deep Reinforcement Learning 에서 Q-learning을 해석하는 과정과 유사하다 위에서 설명한거랑 똑같음!

[!] 정규화: 지수함수를 통해 양수를 만들고 모든 점수의 합이 1을 만들어 확률로 만드는 과정!
[!] 실제 구현시 고려사항: softmax function을 계산할 때 수치적 안정성을 위해 정규화 트릭이 필요(분모와 분자에 동일한 상수를 곱함)

SVM vs Softmax

공통점

똑같은 score vector f(matrix multiplication)로 계산한다. 즉 내적 연산은 똑같이진행한다
score값이 비교가능하지 않음: 같은 classifier과 같은 data 안에서만 loss가 비교 가능할 뿐이다. score가 비교가능한 것과 값에 의미가 있는 것은 다르며 softmax의 경우 score가 의미가 있을 뿐 score가 직접적으로 비교 가능한 것은 아니다

차이점

score 해석 여부

SVM: Class Score으로 해석하여 loss function을 이용해 한 input image x에 대해 정답인 class score가 다른 class score에 비해 margin보다 크도록 만든다
Softmax: 각 class에 정규화되지 않은 log probability으로 해석을 하며 정규화된 log probabilty가 높도록 만들어 loss가 낮도록 만든다. 2.Meaning
SVM: 의미가 없다.
Softmax: 확률로 나타나지기 때문에 의미를 가진다

regulation hyperparameter $λ$ 의 역할

확률이 얼마나 분산되어있는지가 regularization strength( $λ$ 에 의존한다. 즉 일종의 tradeoff가 되며 CS231n 2-3 Linear Classification(Regularization) 다음과 같은 과정으로 어떤 것의 비중이 크게 할지 정한다:

람다의 값이 큼 → W가 큰 값에 패널티를 갖음(Regularization)→ 작은 가중치(W)를 갖게 만듦(일부 가중치들이 매우 작아져서 모델이 더 간단한 구조가 됨!)→ 한쪽에 몰려있는 값(variance)가 줄게됨

람다의 값이 줄어들게 된다면 더 분산된 결과를 갖게 되어 분산이 커진다(regulation의 효과가 적어 모델 학습이 일반화되지만 새로운 데이터에 대한 분류를 제대로 못함)

[!] 람다의 값이 매우 커지면 모든 가중치가 거의 비슷한 크기로 수렴하게 됨(0쪽에 수렴하는 값들이 많아짐)

3. 목적

SVM: local objective로 함수가 각 sample에 대한 loss를 개별적으로 살피는 경향이 있어, 각 data point 주변의 지역적인 정보를 활용하는 방향으로 학습이 된다. 즉 단순한 score값의 비교를 한다
- margin을 만족하면 추가적인 세부조정에 신경쓰지 않는다
- 각 클래스간의 경계를 명확히 나누는데 초점을 둔다(값이 margin보다 작다면 아무런 상관을 안쓰고 0) ex) (10,-100,-100), (10,9,9)똑같이 생각(델타가 1일때)
- 결정경계(decision boundary)를 만들어 샘플 근처의 데이터에 민감하게 만들
Softmax: Class에 대한 확률을 지속적으로 최적화하려는 경향이 있음
- 점수차이에 민감하여 항상 correct class는 높은 확률을 가지려고 하고 incorrect class에 대해서는 낮은 확률을 가지게 만들어 계속해서 loss를 줄이고자 하는 특성이 있다
- 절대 현재 score에 만족하지 않으며 정확한 score을 계속해서 바꾸려고 한다

실제 SVM과 Softmax를 사용할 때 그렇게 큰 차이를 가지고 있지는 않지만 서로 동작방식이 다르다는 것을 알고 있어야한다!

과연 그럼 어떻게 이러한 parameter을 결정할 수 있을까??

🪴 Quartz 4.0

Explorer

CS231n 2-2. Linear Classification (Loss function)

Loss Function

1. Multiclass SVM loss (Support Vector Machine)

SVM loss의 종류

SVM loss의 특징 및 한계점

Multiclass SVM loss동작과정

2. Softmax classifier

정보이론적 관점(Information theory view)에서 바라본 Softmax

확률적 해석(Probabilistic interpretation)에서 바라본 Softmax

SVM vs Softmax

Graph View

Table of Contents

Backlinks