지금까지 배웠던 알고리즘 중 하나인 logistic regression을 Neural Network로 어떻게 해석할 수 있을지에 대해서 알아본 다음에 Neural network에 대해 설명하고자 한다!!
Deep learning: 최근 산업에서 사용이 매우 증가하고 특히 computer vision, natural language processing 등에 사용이 된다. 그렇다면 어떻게 그리고 왜 deep learning의 사용이 증가하게 되었을까?
- Computational power: GPU등을 이용하여 복잡한 computation이 가능하게 됨
- Data available: Internet등에서 데이터들이 많아지게 됨 → 특히 deep learning이 많은 데이터가 있을 때 효과적임
- Algorithm : 새로운 알고리즘이 생기게 됨
Logistic Regression
CS231n 4-2. Setting Up Architecture (Neural Network)
goal 1.0: 사진 속에 고양이를 찾기 (1: 고양이가 존재 0: 고양이 존재X)
- computer science에서 사진은 3차원 정보를 가진다(with RGB, 64X64X3)
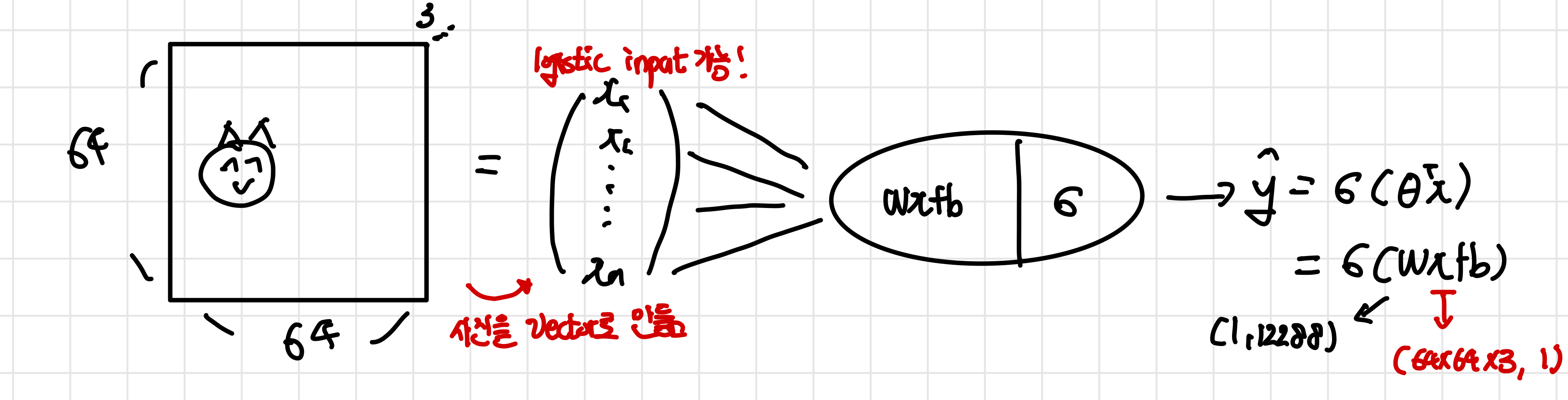 input image가 64X64X3의 크기(픽셀)을 가지고 있을 때 이를 vector로 만들어준다. vector로 만들어야지만 logistic regression에 input으로 들어갈 수 있기 때문이다. 이 값을 특정 weight와 곱해준 후 이 값을sgimoid 를 이용해 값을 0과 1 사이로 만든다.(logistic regression이 classification에 사용) 이때 logistic regression에서 를 이용해 hypothesis를 만들었지만 여기서는 이 값들의 집합인 weight w()로 표현을 한다. 참고로 이때 w의 size는 (1,64X64X3)이 되는데 sigmoid의 input은 하나의 실수 값이어야하기 때문이다.
input image가 64X64X3의 크기(픽셀)을 가지고 있을 때 이를 vector로 만들어준다. vector로 만들어야지만 logistic regression에 input으로 들어갈 수 있기 때문이다. 이 값을 특정 weight와 곱해준 후 이 값을sgimoid 를 이용해 값을 0과 1 사이로 만든다.(logistic regression이 classification에 사용) 이때 logistic regression에서 를 이용해 hypothesis를 만들었지만 여기서는 이 값들의 집합인 weight w()로 표현을 한다. 참고로 이때 w의 size는 (1,64X64X3)이 되는데 sigmoid의 input은 하나의 실수 값이어야하기 때문이다.
이 함수(특히, weight w,b)를 학습시키는 방법은 다음과 같다
- parameters w,b를 초기화 시킨다
- 최적의 parameters w,b의 값을 찾는다 defining loss function(최적값의 proxy-근사값) ➡️ fromMLE 결국 이 loss function을 최소화하는 것이 최적의 parmeter을 구하는 것과 같은 의미를 가짐 using Gradient Descent 각각의 step에서 조금씩 내려가 결국 loss가 최소화되는 지점으로 가게 된다. 를 이용!
- 찾은 최적의 parameter w,b를 이용해 예측을 진행한다
각각의 weight는 위 사진에서처럼 input과 선으로 연결되기 때문에 각 input마다 weight를 곱해서 모두 더해야한다. 따라서 이 logisitic regression의 parmeter의 개수는 12,228+1이다.(input마다 weight가 존재!) 결국 이 parameter는 input size와 연관이 있게 되는데 이도 추후에 수정을 거칠 예정이다.
Neural Network Vocab (neuron & model)
- neuron= linear + activation linear: wx+b 부분에 해당하며 이 linear한 부분에서의 output을 activation function에 넣는다
- model= architecture + parameters 위에서의 예시처럼 one-neuron network라는 architecture와 w,b parameters가 합쳐서 하나의 모델이라고 말한다. 즉, 내가 좋은 모델을 찾았다라는 것은 특정 문제에 알맞는 parameter과 알맞는 architecture을 찾았다는 것이다! 이때 architecture는 neural network등 오늘날 많이 발전했고 parameter들은 오늘날 더 많아졌다
goal 2.0: 고양이/사자/이구아나 사진을 이미지에서 찾기(중복가능)
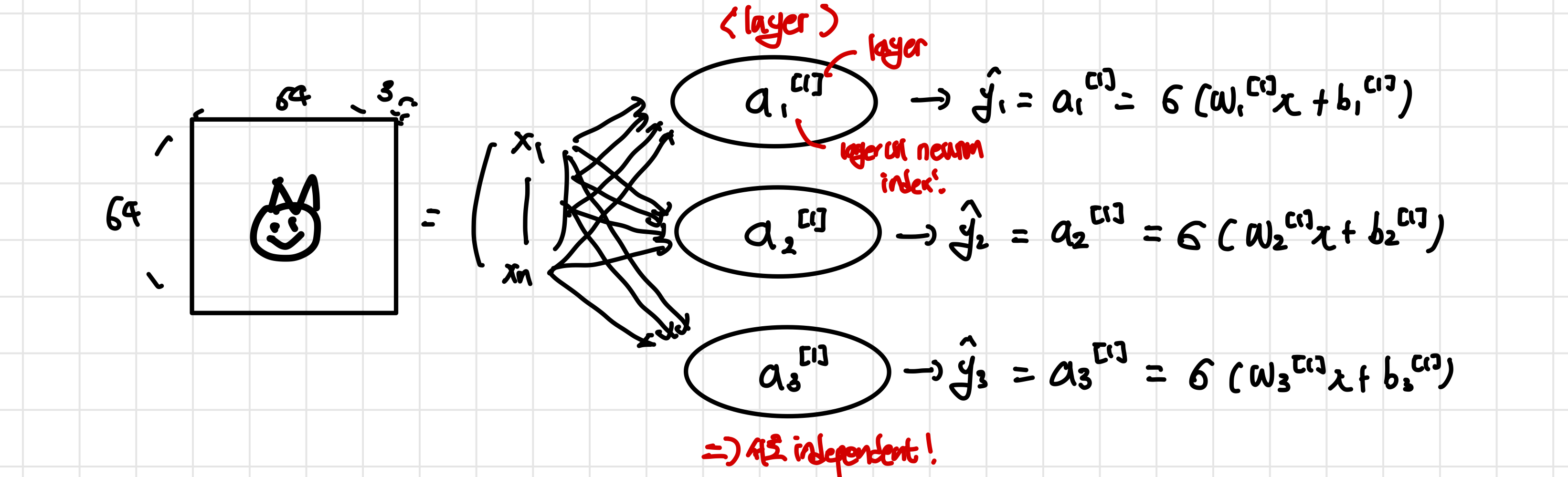 찾아야하는 object가 늘어났기 때문에 그 수에 맞게 새로운 neuron을 추가해준다. 이때 각각의 neuron은 모든 input vector들과 연결이 되어 있고 각각의 neuron은 고유한 parameter 을 가져 이 값이 activaiton function(sigmoid)에 들어가 학습을 진행해 예측을 내놓게 된다.
찾아야하는 object가 늘어났기 때문에 그 수에 맞게 새로운 neuron을 추가해준다. 이때 각각의 neuron은 모든 input vector들과 연결이 되어 있고 각각의 neuron은 고유한 parameter 을 가져 이 값이 activaiton function(sigmoid)에 들어가 학습을 진행해 예측을 내놓게 된다.
이때 같은 input을 공유하는 neuron들의 모임을 layer이라고 하며 layer들 안에 neuron들은 서로 indpendent하다는 특징을 가지고 있다. 그리고 각각의 neuron들은 의 형식을 지니는데 이때 j는 layer의 순서를 나타내며 i는 같은 layer내에서 index를 나타낸다.
이와 같은 모델에서 output은 더 이상 특정 실수가 아닌 vector(여기서는 prediction을 진행하는 가 3개이기 때문에 크기가 3인 vector)가 되고 각각의 neuron은 고유한 parameter을 가지기 때문에 parameter의 개수는 (12288+1)X3이 된다
logistic regression에서는 결국 vector로 표현된 label data가 필요하다. 그렇다면 여기서 각각의 neuron이 어떤 역할은 label vector에서의 object 순서와 관련이 있게 된다. 즉, 특정 순서의 뉴런은 곧 특정 object를 학습을 하는데 그 순서가 label data와 같다는 것이다. (이 예시에서!)
\end{pmatrix}=\begin{pmatrix}p(고양이)\\p(사자)\\p(이구아나) \end{pmatrix}\approx\begin{pmatrix}a_{1}^{[1]}\\a_{2}^{[1]}\\a_{3}^{[1]} \end{pmatrix} $$ 이런 특성 때문에 label이 되는 순서가 달라지게 된다면 각 뉴런이 학습을 하게 되는 object 역시 달라진다. 또한 neural network는 충분한 데이터만 있다면 우리가 알려주지 않아도 알아서 학습하게 되는데, 그래서 하나의 image에 여러가지 동물들이 있어도 이를 학습하여 사진 속에 있는지 없는지 알 수 있다. 또한 이 예시에서는 하나의 layer만 존재하고 이때 neuron들은 서로 독립적이기 때문에 여러가지 동물들을 학습 가능하다. ## goal 3.0 add contraint: unique animal on an image(하나만!) --- 우리가 원하는건 한 object를 정확히 분류하고 이를 이용해 예측을 진행하는 것인데 기존의 방식으로는 여러가지 답이 나올 수도 있고, training example에 특정 object가 적다면학습이 되지 않는 문제가 생긴다. 이런 문제를 해결하기 위해 #Softmax 를 이용해 오직 하나의 object(동물)만을 찾고자 한다! [[CS231n 2-2. Linear Classification (Loss function)]] [[CS229 4. Generalized Linear Model (GLM)]] ![[Pasted image 20240313105632.png]] 가장 큰 변화는 바로 activation function이다. 기존에 sigmoid 함수 대신에 softmax알고리즘을 이용하여 모든 neuron의 output합이 1이 되도록 만들어 각 neuron들이 dependent하게 만든다. 즉, 각 neuron의 output이 단 하나의 object가 뽑힐 확률이 되는 것이고 **일종의 probabilistic distribution이 된다**.(가장 output 값이 높은 것이 해당 사진의 object가 됨). 이때 label data는 goal 2.0과는 다르게 다음과 같이 나타낸다. 그리고 이러한 모델을 *Softmax multiclass network*라고 말한다 $$\text{고양이}\implies\begin{pmatrix}1\\0\\0 \end{pmatrix}\text{ , 사자}\implies\begin{pmatrix}0\\1\\0 \end{pmatrix}\text{ , 이구아나}\implies\begin{pmatrix}0\\0\\1 \end{pmatrix} $$ 참고로 parameter의 수는 goal 2.0에서와 같이 *(12288+1)X3*개가 된다 ## How to train parameters? (loss function) --- **Goal 1.0** :기존 logistic regression에서 loss function의 식은 다음과 같다! $$L=-[y\log{\hat{y}+(1-y)\log(1-\hat{y})}]$$ **Goal 2.0**:하지만 이 식은 문제가 존재하는데 바로. y와 $\hat{y}$ 모두 0 혹은 1의 값을 가지기 때문에 neural network에서의 labdeling을 제대로 할 수가 없다(기존의 식은 하나의 수가 나오는데, neural network에서는 vector가 나와야함) 따라서 loss function을 바꾸면 다음과 같이 바뀐다 $$L_{3n}=-\sum_{k=1}^3[y_{k}\log{\hat{y_{k}}}+(1-y_{k})\log(1-\hat{y_{k}})]$$ 즉, 기존의 loss를 label vector의 size만큼 수행한 것을 더하도록 바뀌었다. 이런 식으로 하여 모든 labeling object에 대해서 loss를 구해 최적화가 가능하게 할 수 있다. 다만 새로운 loss function에서 $\frac{{\partial L_{3n}}}{{\partial w_{2}^{[1]}}}$을 구하는 것과 $\frac{\alpha{\partial}L}{\partial w}$를 구하는 것 사이의 복잡도는 똑같게 되는데, 결국 $L_{3n}$ loss function에서 $w_{2}$에 dependent한 항이 하나밖에 생기지 않기 때문이다. **Goal 3.0**: Softmax loss function 하지만 Softmax에서는 각각의 neuron들이 서로 영향을 미치는(weigth들끼리 서로 영향을 줌!) 일종의 probability distribution이기 때문에 loss function을 미분하는 것이 더 어렵다. 이 loss function을 작성하면 아래와 같고 이를 *softmax cross-entropy*라고 부른다 #cross-entropy_loss $$L=-\sum_{k=1}^3 y_{k}\log{\hat{y_{k}}}$$ 기존 logistic regression에서의 식과 유사하지만 모든 class를 더하고 있다는 것이 다르고 이에 대한 미분(derivates)는 추후에 다룰 예정! 이 loss function은 multiclass classification에서 많이 사용됨! >[!question] **classification이 아니라 regression을 사용해할 때는 어떻게 모델을 바꿀까?** > >예를 들어 사진 속 고양이의 나이를 알고 싶을 때 가능한 방법으로 우리가 기존에 배웠던 ML regression 알고리즘을 사용할 수도 있다. 하지만 우리가 지금까지 알아본 architecture를 어떻게 변형하면 될지 살펴보자! >- **나이의 값은 고유** => Goal 3.0의 softmax architecture을 사용해야함(Goal 2.0은 나이가 여러개 될 수도) >- **activation function의 변화** => 가능한 output의 값이 0보다 큰 실수여야하기 떄문에 sigmoid 함수를 바꿔야한다. 단순히 linear function을 사용할 수도 있고 혹은 #ReLU function을 이용! >- **loss fucntion의 변화** => $\hat{_{y}}-y$ 혹은 $\mid\mid {\hat{y}-y}^2$ 을 이용해 regression에서 최적화를 더 쉽게 만들어 줄 수 있는 loss function으로 바꿔줌 # Neural Network ## Model --- goal: 이미지에 고양이가 있냐없냐!! 기존의 architecture에서 layer들과 neuron을 추가했다. 이때 **parameter의 개수는 input data의 개수와 관련이 있기 때문에 layer2와 layer 3에서는 각각 (그 전 단계의 output+1) X (layer의 개수)** 가 된다. 그리고 대부분의 neural network가 그렇듯 앞쪽 layer이 차지하는 parameter 개수의 비중이 높다 ![[Pasted image 20240313143605.png]] 이때 *layer* 은 서로 연결되지 않는 neuron들의 집합이라고 볼 수 있으며 cluster of neurons라고 일컷는다. input layer은 맨 첫번째 layer, output layer은 맨 마지막 layer을 뜻하며 그 사이에 있는 모든 layer들을 hidden layer이라고 부른다. (input이 무엇인지 잘모르는 abstraction한 상태) 이 hidden layer에서 무엇이 일어나고 있는지 알 수는 없지만 충분한 데이터가 있다면 효과적으로 학습을 진행함 [[CS231n 12. Visualizing and Understanding]] 에서 이 hidden layer가 어떤 뜻을 가지고 있는지 알아보고자 함! >[!question] **architecture의 구조(layer의 수 등)은 어떻게 정해?** > >어떤 architecture가 가장 좋은지, 특히 layer의 수가 몇개가 필요한지는 아무도 알 수가 없다. 다만 cross validaiton과 같이 직접 성능을 평가를 하면서 layer이나 neuron의 개수등를 직접 알아봐야한다. (**Neural Network model= Architecture + Parameter인데 Parameter은 뒤에 나올 propagation과 gradient등을 이용해 최적화된 값을 알 수 있다** ) >그렇기 때문에 *주어진 문제의 복잡도(complexity)*를 미리 예상을 한 뒤 그에 맞는 architecture size를 정하는 것이 좋다! 주로 **input layer**은 이미지의 근본이 되는 개념에 대해서 학습을 진행하여 주로 *edge*로 나타난다.(pixel 단계에서 이들을 가지고 학습한 결과 edge정도를 구별할 수 있게 됨!).그리고 **hidden layer**에서 각각의 결과들을 합쳐 또 다른 결과를 얻어낸다.(귀, 입과 같이 고차원의 정보) 특히 neuron이 많고 layer들이 더 많을 수록 더 고차원의 학습을 할 수 있다. 그 후 마지막으로 **output layer**에서 찾고자 하는 object의 모습을 학습하게 됨 ![[Pasted image 20240313143526.png]] 위 그래프는 neural network의 각 layer에서어떤 일이 일어나고 있는지를 이해하기 쉽도록 만든 예시이다. 집 값을 예측하려는 모델을 만들 때 여러가지 input이 합쳐져 새로운 관계를 찾을 수 있다. 예를 들어 침실의 수와 집의 사이즈를 통해 가족 구성원의 수를 학습하고 이것을 집값과 연결지을 수 있다는 것이다. 여기에 fully-connected layer로 만든다면 우리가 알지 모르는 특성들을 network가 알아서 학습할 수 있다 >[!note] **Neural network의 별칭** > neural network는 주로 **black box** 모델이라고 얘기를 많이한다. 그 이유로는 hidden layer가 어떻게 학습을 진행하거나 무엇을 진행하는지 전혀 알 수 없고 단지 도출해낸 결과가 최선이라고 설명을 하기 떄문이다 또한 **end to end learning** 이라고도 불리는데 input과 output만을 알 뿐 나머지는 알 수 없기 때문이다. 이러한 별칭에서 벗어나기 위해 [[CS231n 12. Visualizing and Understanding]]에서와 같이 여러가지 시도를 하는 중이다. ## Propagation equation [[CS231n 4-1. Backpropagation (gradient for neural network)]] 각 parameter들, neuron에서의 linear 부분과 activation function 부분을 (vector)을 통해 나타나면 다음과 같다 $$\begin{aligned} \text{1. }\underbrace{ z^{[1]} }_{ (3,1) }=\overbrace{ w^{[1]} }^{ (3,n) }\underbrace{ x }_{ (n,1) }+\underbrace{ b^{[1]} }_{ (3,1) }\text{ , } a^{[1]}=\sigma(z^{[1]})\\ \text{2. }\underbrace{ z^{[2]} }_{ (2,1) }=\overbrace{ w^{[2]} }^{ (2,3) }\underbrace{ x }_{ (3,1) }+\underbrace{ b^{[2]} }_{ (2,1) }\text{ , } a^{[2]}=\sigma(z^{[2]})\\ \text{3. }\underbrace{ z^{[3]} }_{ (1,1) }=\overbrace{ w^{[3]} }^{ (1,2) }\underbrace{ x }_{ (2,1) }+\underbrace{ b^{[1]} }_{ (1,1) }\text{ , } a^{[3]}=\sigma(z^{[3]}) \end{aligned}$$ 괄호로 들어가 있는 것은 vector의 크기를 나타내며 우리는 이것을 더욱 **vectorize**할 것이다. #stochastic gradient와 #batch gradient의 차이점을 생각해보면 stochastic gradient는 하나의 example만을 보고 update를 진행해 noisy하다는 문제점이 있는 반면에 batch gradient는 모든 example들을 본 뒤에 update를 진행하기 떄문에 더 정확하다. ### Input batch! m개의 example들의 input batch에게 어떤 일이 일어날까? 하나의 example들을 가지고 gradient를 구하는 것이 아니고 모든 example들을 한번에 확인해서 gradient를 진행해야하기 떄문에 새로운 matrix X를 정의한다. (X는 모든 example들의 vector 값들이 모여져있음) $$X=\begin{pmatrix} \vdots &\vdots &\vdots\\ x^{1} \ & x^{2} {\text{}}\dots \ &x^{(m)} \\ \vdots&\vdots&\vdots \end{pmatrix}$$ 이때 neuron의 linear한 부분(gradient 계산이 되는 부분)을 살펴보면 아래와 같이 식이 나타내지는데 형태는 같지만 각 vector의 크기가 상이하다. 또 layer이 많아질수록 연산시간이 오래걸리기 때문에 식을 최대한 일정하고 간단하게 만들었다. **이때 input의 개수가 얼마이든지 상관없이 parameter의 개수는 똑같다**. 그렇기 때문에 w와 b의 크기가 각각(3,n), (3,1)로 고정이 되는 것이다. 하지만 여기서 문제는 바로 b인데 3Xn matrix와 3x1 vector사이에 덧셈 연산이 불가능하기 떄문이다! $$\begin{aligned} \underbrace{ Z^{[i]} }_{ (3,m) }&=\underbrace{ w^{[i]} }_{ (3,n) }\overbrace{ X }^{ (n,m) }+\underbrace{ b^{[i]} }_{ (3,1) }\\ &= \begin{pmatrix} \vdots &\vdots \\ z^{[1][1]} \dots &z^{[1][m]} \\ \vdots &\vdots \end{pmatrix} \end{aligned}$$ *broadcasting*을 이용하는데, parameter의 수는 바꾸지 않지만 위 연산이 가능하도록 바꾸는데 사용이 된다. 이때 똑같은 b를 m번 써줌으로써 matrix로 만들어 문제를 해결한다. (식을 최대한 간단하고 일정하게 사용하도록 만듦) 참고로 numpy에서는 #broadcasting 을 사용자가 구현하지 않아도 자동으로 broadcasting을 해서 연산이 됨 $$\tilde{b^{[i]}}=\begin{pmatrix} \vdots &\vdots \\ b^{[1]} \dots &b^{[m]} \\ \vdots &\vdots \end{pmatrix} \implies \text{column의 개수가 m개}$$ 즉, 이를 통해 식들을 대문자 변수들로 만들어서 최대한 간단하게 표현이 가능하여 연산 효율의 향상을 가져올 수 있다 ## Parameters! (Optimization) ### Loss function --- 앞서 세운 식은 propagation equation이라고 부르며 forward propagation이라고 우리는 부른다. 여기서는 각 step마다 loss를 구하기 위한 gradient를 구하는 식을 사용할 것인데 이 과정을 backward propagation이라고 부른다. 이때 우리가 하고자 하는 것은 parameter들의 최적화된 값을 찾는 것이고 그러기 위해 우리는 loss/cost function을 사용한다. 참고로 **loss function**은 batch에 하나의 example만 존재할 때, **cost function**은 batch에 여러개 example이 있을 때 사용되는 용어다. cost function을 정의하면 $$\begin{aligned} \overbrace{ \hat{y}=a^{[3]}=\sigma(z^{[3]}) }^{ \text{마지막 layert의 output} }\text{ 일때, } J(\hat{_{y}},y)=\frac{1}{m} \overbrace{ \sum_{1}^m L^{(i)} }^{ batch! }\\ \text{ with } L^{(i)}=\underbrace{ -[y^{(i)}\log{\hat{y^{(i)}}}+(1-y^{(i)})\log(l-\hat{y^{y^{(i)}}})] }_{ \text{logistic loss!} } \end{aligned}$$ 즉, propagation과정에서 parallized된 식등을 통해 모든 example을 보는 batch gradient를 진행하여 cost funtion을 계산하고 gradient의 방향을 정한다. >[!important] $\frac{{\partial J}}{\partial w^{[2]}} \text{ VS } \frac{{\partial L}}{\partial w^{[2]}}$ > >**이 neural network의 cost function은 기존의 logistic loss를 단순히 더한 형태이다(linear!)**. 그렇기 때문에 결국 logisitc loss L를 $w^{[2]}$에 대해 미분하는 것과 loss function J를 $w^{[2]}$에 대해 미분하는 것이 같은 복잡도를 가지고 있다. *결국 모든 미분값을 J에서 계산하지 않고 L에 대해서 계산을 해도 같은 결과가 나오게 된다!* ### Backward Propagation [[CS231n 4-1. Backpropagation (gradient for neural network)]] loss function을 정의했기 때문에 backward propagation을 통해 optimization을 진행한다! **이때 시작은 가장 output과 가까이 있는 layer에 대해서 진행하는데(output layer)**, 우리가 알고 있는 것은 전체 function의 loss이기 때문에 가장 거리가 가깝고 중간에 우리가 계산하지 못하는 parameter가 없기 떄문이다. 이 예시에서는 w3와 loss function의 관계로부터 시작한다 $$\begin{aligned} { z^{[1]} }={ w^{[1]} }{ x }+{ b^{[1]} }\text{ , }& a^{[1]}=\sigma(z^{[1]})\\{ z^{[2]} }={ w^{[2]} }{ x }+{ b^{[2]} }\text{ , }& a^{[2]}=\sigma(z^{[2]})\\ { z^{[3]} }={ w^{[3]} }{ x }+{ b^{[3]} }\text{ , }& \hat{y}=a^{[1]}=\sigma(z^{[3]})\\ \end{aligned}$$ 인 상황에서 각 parameter에 대해서 미분을 진행하면 다음과 같이 나타낼 수 있다 ![[Pasted image 20240314112502.png]] 즉, 기존의 계산한 것들을 이용해서 새로운 parameter의 gradient를 구할 수 있고 나머지 따로 구해야하는 부분은 연산하기 쉬운 부분만 남는다. 즉, chain-rule을 이용해 쪼개서 gradient를 구하고 여기서 구한 값을 재활용함으로써 효율적으로 backward propagation을 진행한다