CS231n 2-3 Linear Classification(Regularization)

loss만을 이용하여 loss function을 만들었을 때의 문제점은?

weight W가 loss가 0을 만들어낸다면 (특히 SVM) loss가 0인 여러 다른 W가 있을 수 있다. a>1인 a에 대해서 aW 역시 값을 0으로 반환하여 같은 결과를 낼 수 있기 떄문이다. score 역시 a만큼 증가시키게 되고 이로 인해 절대적 차이 역시 똑같이 scaling 되며 만약 a<1이면 차이가 줄어들어서 SVM에서 loss 값이 증가하게 되어 0이 아니게 될 수 있다.

그렇다면 여기서 문제가 생기는데 여러 W가 모두 loss를 0으로 만든다면 어떤 W가 가장 좋은 W일까? 그리고 loss를 최소로 만드는 W가 있다고 하더라도 이 W가 실제 학습에서 분류를 잘하게 만드는 W일까?

실제로 loss를 최소로 만드는 W의 경우 train data에 대한 과적합(overfitting)의 위험이 있으며, 결국 모델이 하고자 하는 바는 새로운 데이터가 들어왔을 때 얼마나 잘 분류하느냐이기 때문에 정확도가 높은 것(loss가 낮은 것) 뿐만 아니라 모델이 얼마나 일반적이며 단순한지가 중요하다는 것이다.

즉, W의 차원성이 높아지면 classifier가 고차원에서 학습을 하게 만드는 가능성을 열어주지만 너무 복잡해져서 실제 test data에 대한 성능이 떨어질 수 있으므로(soft penalty) regularization 항이 추가하여 더 정확성을 높이는데 도움을 줄 수 있게 한다. 결국 1) 차원이 높아지면서 발생하는 복잡성과 2) 그로 인해 성능이 좋아지는 것 사이의 trade off를 통해 성능을 향상시키게 만드는 항이라고 생각하면 된다.

Regularization

위에서 제기한 질문과 같이 loss를 최소로 하는(혹은 0인) 여러가지 W가 같은 결과값을 낼 수 있기 때문에 이러한 모호성 (ambiguity)을 해결해야한다. 이 뜻은 곧 W가 하나의 값으로 일반화하지 못해 새로운 데이터에 대한 일반화 성능이 보장하지 못한다고 볼 수 있다. 이런 경우애는 어떤 feature가 중요한지, 어떤 패턴을 학습했는지 확인하기 어려우며 과적합(overfitting)의 위험도 존재한다

• [!] 다시 간단히 정리하자면 loss만을 최소로 하게 할 경우 다음과 같은 문제가 생기게 된다
  1. 같은 값을 만들게 하는 W로 인해 모호성이 생긴다 ➡️ Test data에 잘 맞기 위한 더 simple한 W를 원함
  2. loss가 0은 곧 training data에 완벽한 W이므로overfitting 을 유발할 수 있다 ➡️ overfitting 문제를 해결해야함
  3. training data를 완벽히 학습하는 것이 목표가 아니다 ➡️ 중요한 것은 train set이 아닌 test data에서의 성능임

즉, loss가 0인 것이 항상 좋은 것이 아니며 다음과 같은 문제들을 해결하기 위해 W값에 대해 평가하는 Regularization 항이 loss function에 필요하다는 것을 알 수 있다.

$R(W)$: Regularization 항의 추가!

• 결국 이 regularization 항이 어떤 역할을 하는지 간단히 말하자면 이 penalty가 있는데도 너가 복잡한 모델을 계속 쓰고 싶으면 이 penalty를 감수해야할거야! 이라고 나타낼 수 있다.
• $R(w)$는 오직 W(weight)에만 영향을 받고 입력받은 데이터에 영향을 받지 않음
• 패널티를 어떻게 줄 것인지 정하는 부분에 대해서는 여러 함수에 따라 다르게 나타날 수 있으며 이는 바로 아래에서 간단하게 다룬다.

참고로 W와 다르게 b(bias)는 input 차원과 관련이 없기 때문에 이를 regularize하지는 않는데 이는 bias의 역할이 단지 각 class의 의존성을 줄여주는 것일 뿐 학습 과정에서 일반화에 영향을 주지는 않기 때문이다. 또한 $R(W)$ regularization 항의 추가로 인해 loss가 0이 될 가능성이 없어졌다(W=0일때만 가능해짐)

Regularization 종류

단순 classifier에서 가장 많이 사용되는 regularization 함수는L2L1 함수이며, 딥러닝에서는dropout 을 통해 regularization을 구현한다.

• L2 regularization: $R(w)={\sum }_k{\sum }_l{W}_{k,l}^2$ ⇒ 주로 가장 많이 사용이 된다
• L1 regularization: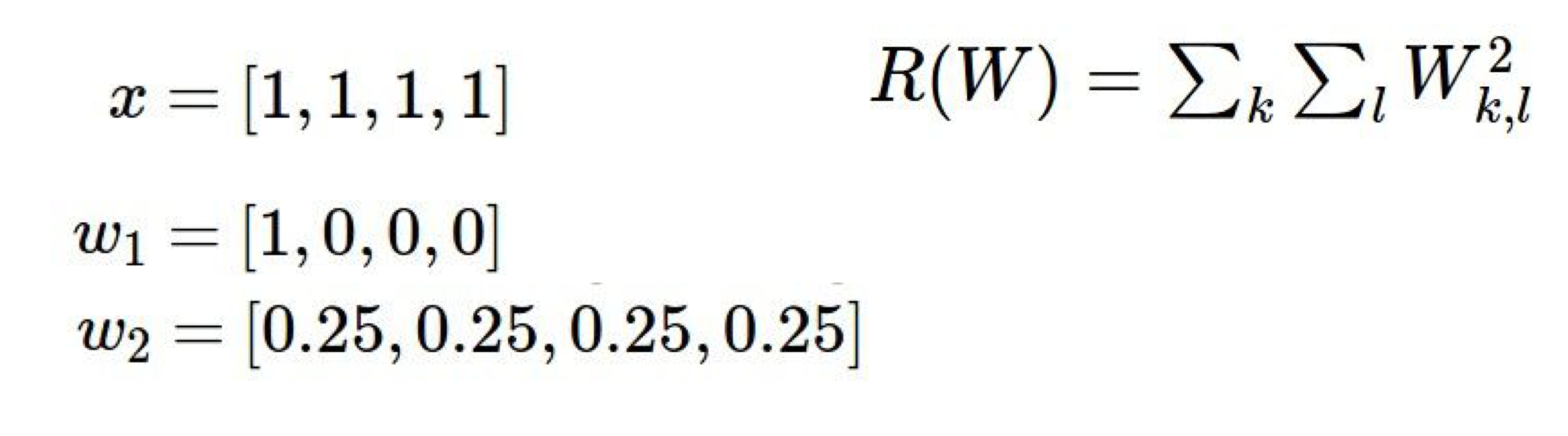 $R(w)={\sum }_k{\sum }_l|W_{k,1}|$

1. L2 regularization: 가장 흔한 regularization penalty R(W)로, parameter W안에 있는 모든 항에 대해 자기자신을 제곱하여 더한다. L1과 구별되는 가장 큰 특징은 큰 가중치를 가지는 것에 대해 더 많은 패널티를 부과하는 것으로 이것이 w의 간단함, 모델의 단순함을 더 효과적으로 표현할 수 있어 더 일반적인 regularization이 되는 것 같다.
   • max margin(최대특성마진)을 만드는 경향이 있음
   • ⭐️큰 가중치에 페널티를 부과해 generalization(일반화) 을 이끈다.
     • 큰 가증치 패널티 ➡️w 값이 고르게 분포 ➡️ w가 input x 값을 고르게 영향을 받아 결과 도출 ➡️ 학습에 유리
     • 큰 가중치 패널티 적음 ➡️ w 안의 특정 부분에만 값이 몰림 ➡️ w가 input x에 특정 값만을 고려하여 결정 ➡️학습에 불리
   • 가중치의 크기를 제한하여 하나의 특성이 너무 큰 영향력을 갖지 않도록 방지하며 특정 특성에 독립적인 중요도 감소하게 만들어 모델이 최적화 과정에서 큰 가중치를 줄이는 경향이 있음
   • 과적합(overfitting) 방지
     1. 같은 Score을 가지고 있더라도 고른 분포의 경우 제곱의 합이 더 적은 경향이 있음
     2. 결정이 여러 분산되어있는 값들을 통해 이루어짐 ⇒ generalization(일반화) 개선하게 됨

• [?] CS229 8. Data Splits, Models & Cross-ValidationBayesian : 만약 bayesian이라면 L2 regularization이 Gaussian prior을 따르는 W를 이용하여 MAP 추론과 상응할 수 있다

2. L1 regularization
   • sparse한 solution을 고르게 됨(0이 많고 특정 부분에만 값이 몰려있게 만듦) ⇒ 어떻게 복잡도를 구해야하는지에 따라 L1과 L2의결정이 달라질 수 있음
   • 0이 많으면 좋다고 생각!

Full Mulitclass SVM loss 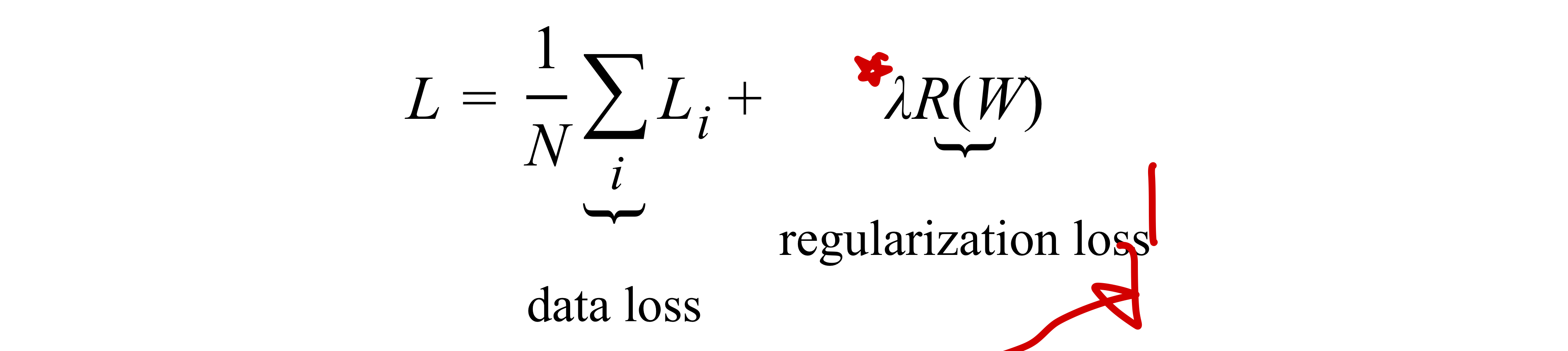Squared L2 norm을 이용한 loss fuction 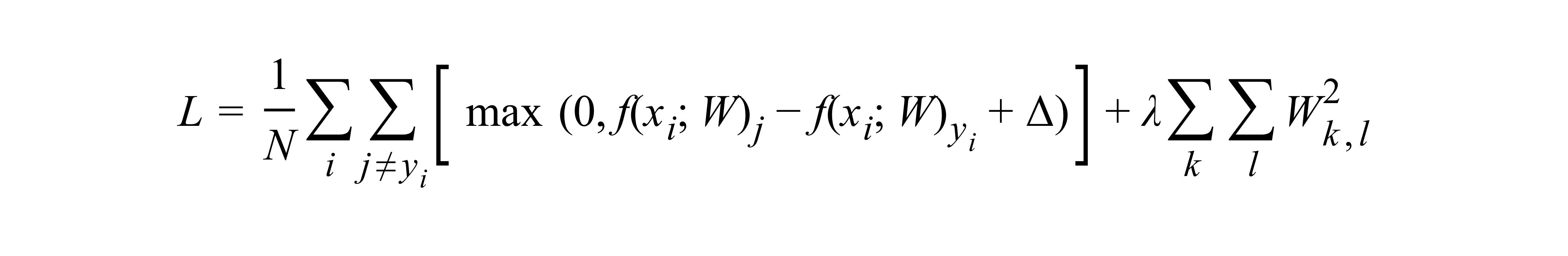여기에서 언급되는 람다를 지정하는 단순한 방법은 없고Cross_Validation 을 통해서 주로 결정된다 14-1. Cross Validation

Practical Consideration

1. 람다 설정: 데이터 손실(델타)과 정규화 손실(람다) 사이의 균형을 맞추며 무엇에 더 비중을 둘지 정하게 만드는 일종의 trade-off 역할을 한다. CS231n 2-2. Linear Classification (Loss function) SVM VS Softmax 부분에서 이와 관련해 간단히 설명하는 부분이 있다.
   • 실제 점수에 직접적인 영향을 미치지 않음
   • 중요한 것은 람다를 이용한 regularization의 비중 정도를 통해 가중치의 크기(Weight)를 얼마나 허용할지이며 어차피 data loss에서는 람다($\lambda$)가 바뀌는 것이 의미가 없고 regularization에서만 의미가 생기게 됨
2. 이진 SVM과의 관계:
3. 최적화 관련 사항: 제약이 없는 원형태의 최적화 목표를 다룸
   • 부분 기울기(sub gradient)를 사용하는 것이 일반적
4. 다른 다중 SVM 형식: 일대다(ONA: 클래별 독립적인 이진 SVM), 다대다(모든 클래스간 이진분류)

CS231n 2-2. Linear Classification (Loss function)