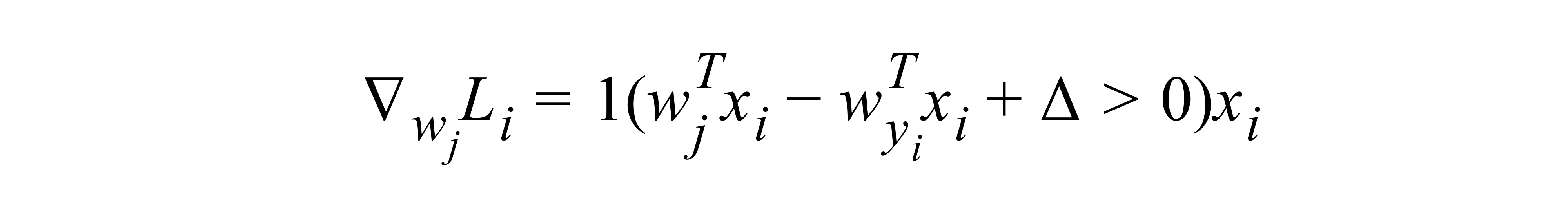CS231n 4-1. Backpropagation (gradient for neural network)

그렇다면 복잡한 모델에서 어떻게 weight들이 optimization될까?

앞선 강의에서는 결국 analytic gradient의 방법으로 gradient descent를 하는 것이 가장 효과적인 최적화(opitmization) 방법이라는 것을 말했다. 그렇다면 단순한 함수가 아니라 복잡한 함수들, 그리고 여러가지 layer들을 지나갈 때 어떻게 gradient들이 전달되고 이로 인해 weight W들이 바뀌게 될까? 이번 강의에서는 이와 관련하여 computational graph를 만들고 이를 통해 backpropagation을 하는 것에 대해 다룬다.

우리가 이 강의에서 알아보고자 하는 것은?

---

실제로 앞서 다룬analytic_gradient 를 어떻게 계산하는지에 대해 알아볼 것이다.! 앞으로 다룰 Neural Network는 여러개의 linear classifier을 사용하며 이로 인해 각 layer마다 weight가 존재하게 된다. 그렇다면 어떻게 수많은 weight들의 gradient를 찾을 것인가?

input data $x_i$에 대해 gradient 계산이 쉬울지라도 실제로는 parameter $W$에 대한 gradient를 주로 계산하게 되는데 이 계산된 gradient 값을 토대로 다시 parameter $W$를 업데이트 하는 과정을 반복한다. 후에 neural network가 어떻게 작동,해석,시각화하는지에 대해 $x_i$의 gradient에 따라 활용될 수 있으며 이를 위해backpropagation(역전파) 방법이 필요하다! CS231n 3. Linear Classification (Optimization)

이때 backpropagation(역전파)는 네트워크 전체에 대해 Chain rule(연쇄 법칙)을 적용하여 gradient를 계산하는 방법 중 하나 중 하나로 neural networks을 효과적으로 개발, 디자인 및 디버깅 하는데 중요하다.

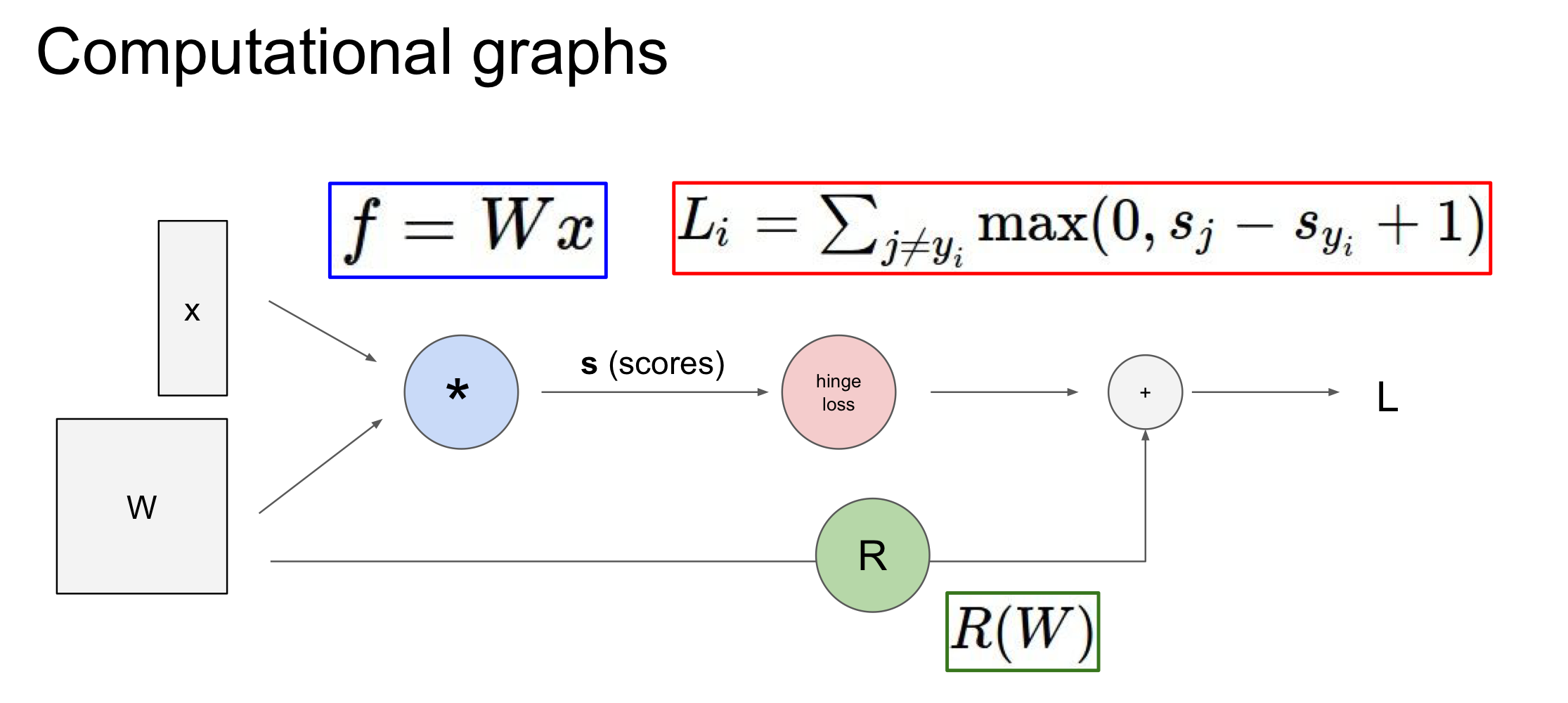
Computational graph

---

Computational Graph는 모델의 input 및 함수, loss등과 같이 전반적인 과정을 graph로 나타내는 것으로 가장 강력한 점은 파악하기 어려운 그 어떠한 함수도 이러한 graph를 이용해 간단히 분해하여 chain rule을 통해 backpropagation을 쉽고 빠르게 구할 수 있다는 것이다! 즉, input value ,local gradient, 복잡한 형태의 analytic gradient를 쉽게 계산하여 update에 용이하게 만든다

Backpropagation 과정

---

일단 gradient를 어떻게 구할 것인지만을 알아보고 이것이 어떻게 update가 되는지는 나중에 알아보려고 하며 결국은 gradient를 얻기 위해서 어떤 과정이 필요한지를 다룬다

1. 전체 과정(함수)에 대한 computational graph 만들기
   • 변수와 미분가능한 연산을 미리 만들어 node를 만들어놓아야 한다. 즉, 복잡한 함수 f를 덧셈과 곱셈 등의 미분가능한 독립적인 node를 만들어 gradient를 구할 수 있도록 설계를 해야한다.
2. 각 local gradient 구해놓기 : 이때 대부분의 경우 node가 곱셈 혹은 덧셈과 같은 형태이기 때문에 미리 local gradient의 값을 구해놓을 수 있으며 이로 인해 위쪽에서 gradient(단순한 숫자)를 받게 되면 바로 계산이 가능해진다. 즉, local gradient를 더 간단한 형태의 값으로 바꾸어 저장을 하게 된다.
3. 최종 loss $L$은 forward pass의 과정이 완료되면 구해지게 됨
4. 구한 loss $L$을 가지고 기존에 구한 local gradient를 이용해 chain rule을 이용해 gradient를 계산
5. 최종 목적지는 input과 weight에 대한 gradient를 구하는으로 뒤쪽으로 오면서 gradient를 계속 계산

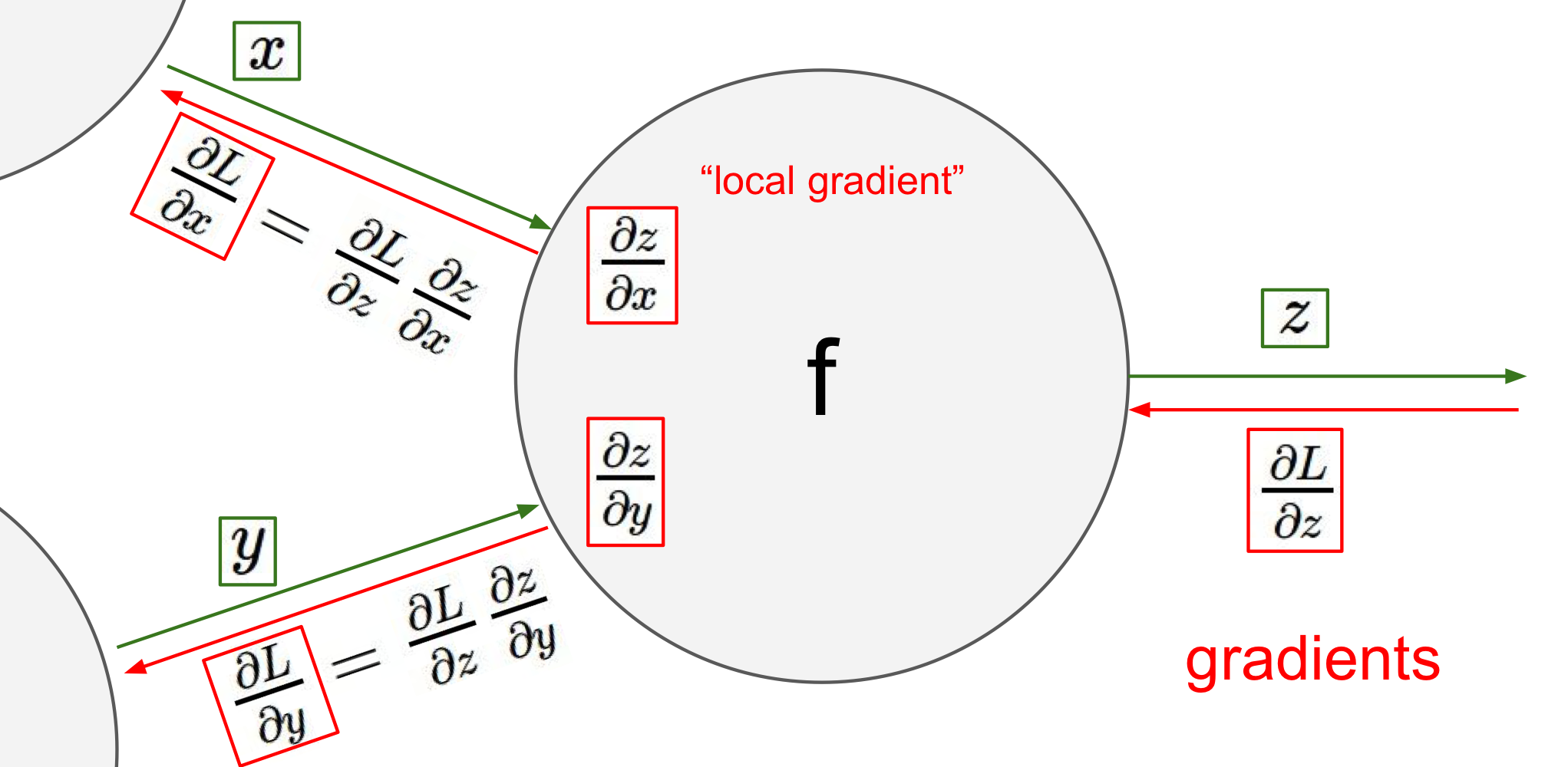
<하나의 node에서의 backpropagtion 과정>

Example 1) 기초

---

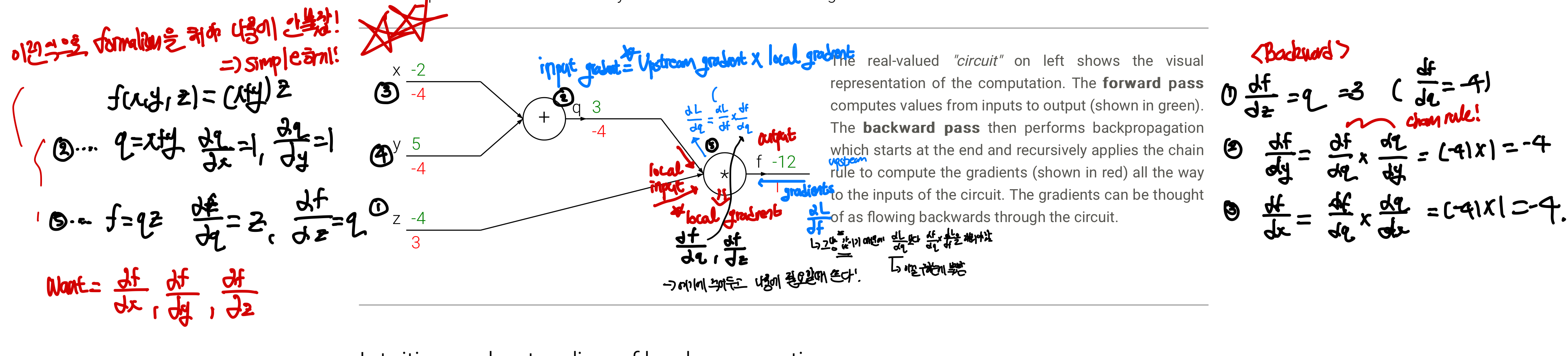$f(x,y,z)=(x+y)z$ 변수는 $x,y,z$이며 이때 함수 $f$를 미분 가능한 단순한 연산으로 바꾸면 $+$와 x

1. computational graph 그리기: 변수에서 시작하여 미분 가능한 연산들이 독립적인 node로 형성되어 추후에 합쳐짐
2. local gradient 구하기: $dq/dx=1$, $dq/dy=1$, $df/dq=z$, $df/dz=q$
3. chain rule: $df/dy=df/dq•dq/dy=(-4)X1=-4$

이때 얻어지는 gradient의 부호는 어떤 의미를 가질까?

이 부분에서 알 수 있는 것은 x와 y는 현재 음의 gradient를 가지고 있는데 이는 곧 4의 힘으로 낮아지기를 원한다고 볼 수 있다. 즉, x와y가 현재의 값보다 더 작은 값으로 이동해야 loss가 감소한다는 뜻이다

ex) x,y가 음의 gradient➡️ x,y 감소➡️ 덧셈gate 출력이 감소➡️곱셈게이트 출력이 증가

• [!] backpropagation은 보다 loss가 최소가 되도록 게이트들이 자신들의 출력을 얼마나 강하게 증가/감소해야하는지 알려주는 과정이라고 볼 수 있다.

Example 2) Sigmoid

---

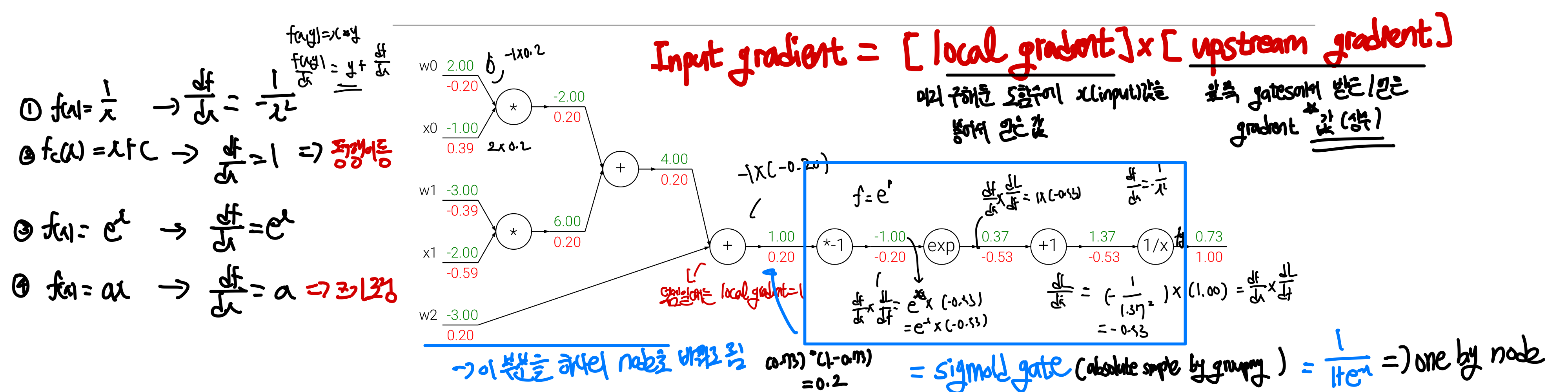
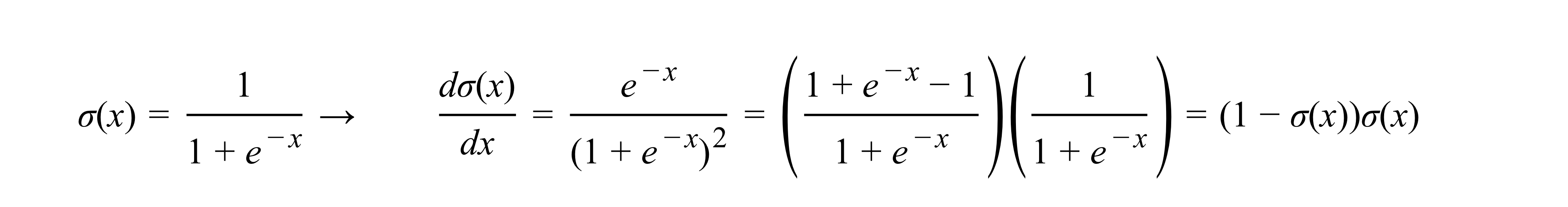이를 통해 알 수 있는 점은 위에sigmoid 예제처럼 간단한 형태로 미분 가능한 식을 알고 있다면 연산 gate를 여러가지로 만들필요 없이 하나로 줄일 수 있다는 것이다. 결국 1) 내가 수학적 능력을 이용하여 더 간편한 graph를 설계할지 아니면 2) 얼마나 간단하게 각각의 local gradient를 구할 수 있는지는 일종의 trade-off라고 볼 수 있다. 즉, graph를 어떻게 설계할지는 상황에 따라, 사람의 능력과 취향에 따라 달라진다

• [!] Input gradient=[local gradient]X[upstream gradient]
  • local gradient: input으로 들어오는 gate들에 대해 간단한 식으로 미리 만들어놓은 도함수
  • upstream gradient: 위쪽 gate에서 받은 gradient 값으로 상수

즉, 이런 식으로 local gradient를 알고 있다면 backpropagation을 통해 복잡한 형태의 함수도 각 weight들과 input 값들이 어떤 식으로 변화해야하는지를 쉽고 빠르게 알 수 있게 된다.

각 gate의 역할

• max gate:gradient router z와 w 두 값이 max gate에서 만난다고 할 때 z>w면 z의 local gradient는 max gate 위쪽에서 받아온 gradient값이 될 것이고, w는 0이 될 것이다. 즉, gradient를 여러가지 길 중에 한쪽으로 보내주는 router의 기능을 한다. 이는 CS231n 3. Linear Classification (Optimization)에서 SVM을 미분했을 때의 식을 보면 알 수 있으며 max값만이 살아남아 loss까지 가므로 gradient도 max값에만 존재하게 된다.
• 
• add gate:gradient distributor gradient의 값을 똑같이 나눠준다
• mul gate: gradient switcher 곱의 미분법에 따라 local gradient가 다른 gate의 결과값에 의해 영향을 미친다

Example 3) ⭐️ input이 vector일 경우(상수X)

---

이럴 경우 gradient가 아닌jacobian 으로 계산하면 된다 이때 Jacobian Matrix는 여러개의 함수들이 여러개의 변수들에 대해 어떻게 변화하는지를 나타내는 수학적 도구로, 주로 다변수 함수의 미분을 다룰 때 사용하며, 함수의 각 변수에 대한 편미분을 모은 행렬이다.

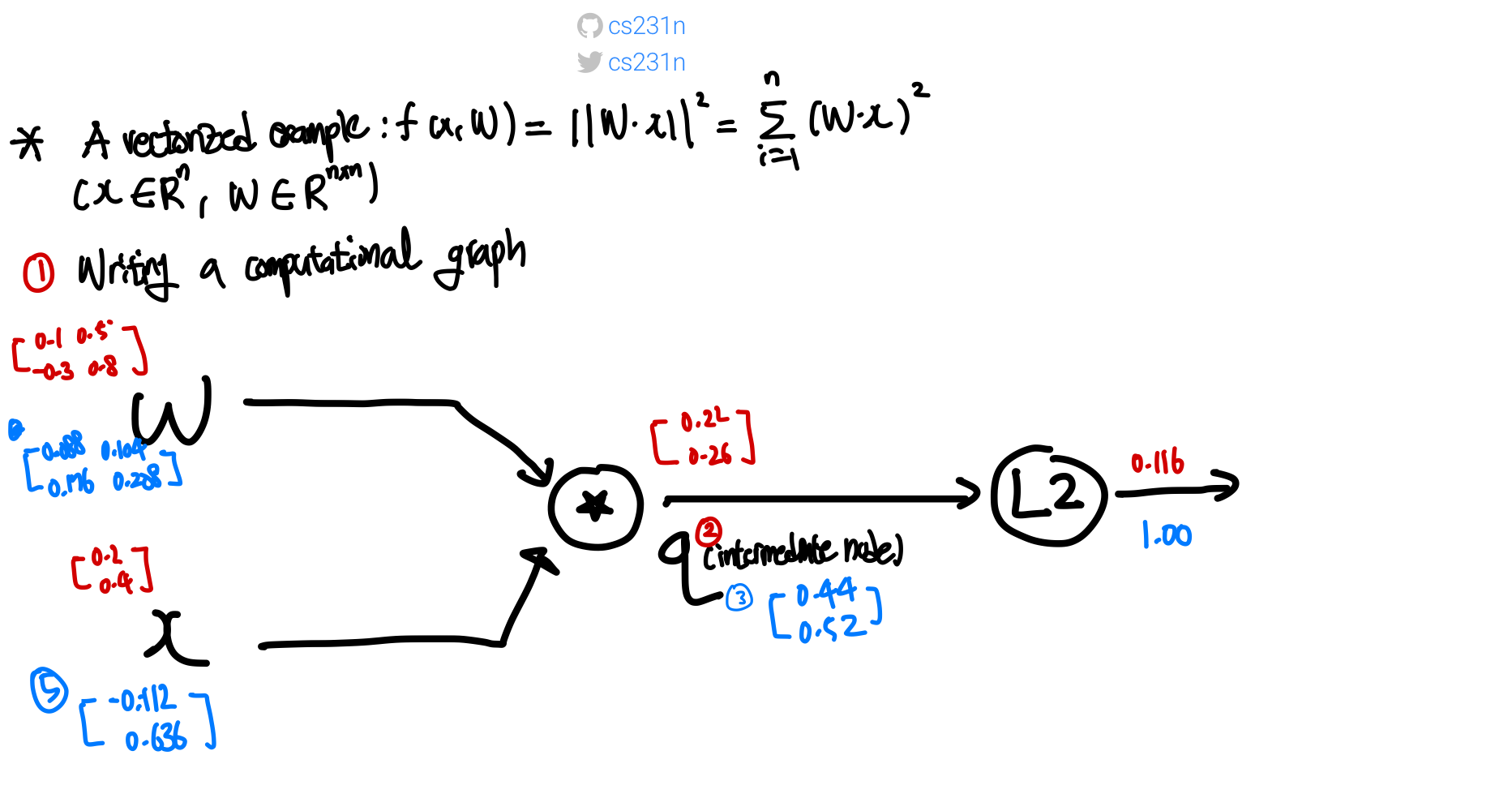
1. computational graph를 구한다
2. mul gate의 node 이름을 q라고 하며. $q=W•x=\left(\begin{array}{c}{W}_{1,1}{x}_1+\cdots +W_{1,n}{x}_n\\ W_{n,1}{x}_1+\cdots +W_{n,n}{x}_n\end{array}\right)$ , L2 gate에서는 $f(q)=||q|{|}^2=q_1^2+\cdots +q_n^2$으로 표현이 가능하다.
3. 최종 loss가 1이라고 한다면 L2 gate에서 local gradient가 ${\nabla }_{q}f=2q$이기 때문에 q값의 2배가 곧 local gradient가 된다
4. q gate는 mul gate이므로 local gradient값이 다른 input gate에 영향을 받게 된다. input W에서 local gradient는 $\frac{d{q}_k}{d{W}_{i,j}}=1_{k=i}{x}_j=\left[\begin{array}{c}0.2\\ 0.4\end{array}\right]$ 이 되며 $\frac{df}{d{W}_{i,j}}={\sum }_{k}2q_k(1_{k=i}{x}_j)=2q_i{x}_j$ 즉, ${\nabla }_{w}f=2q\ast x^T$ 가 된다. 2X1 X 1X2이므로 총 2X2 matrix인 $\left[\begin{array}{cc}0.88& 0.104\\ 0.176& 0.258\end{array}\right]$ 만들어진다
5. 마찬가지를 input x에서 local gradient는 $\frac{d{q}_k}{d{x}_i}=W_{i,j}=\left[\begin{array}{cc}0.1& 0.5\\ -0.3& 0.8\end{array}\right]$ 이 되며 $\frac{df}{d{x}_i}={\sum }_{k}2q_k{W}_{k,i}$, 즉 ${\nabla }_{x}f=2W^T\ast q$ 2X2 X 2X1이므로 2X1 matrix가 만들어진다

• [!] variable과 관련된 gradient에서 항상 variable과 같은 차원인지를 확인해야하며 ⭐️chain rule에서 무엇을 먼저 연산을 해야할지 차원에 맞추어 확인해야한다!

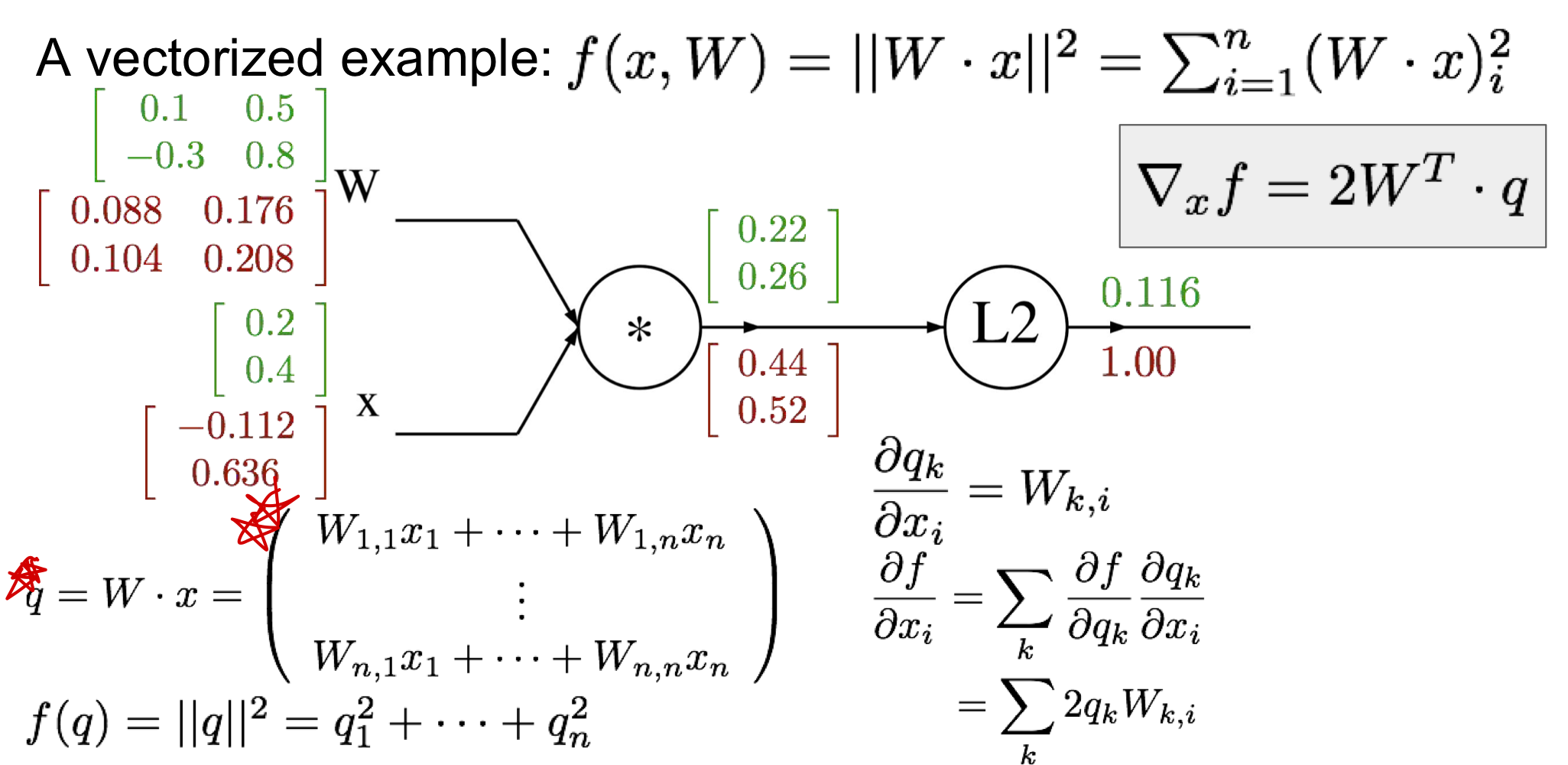백터의 gradient는 항상 원본 백터의 사이즈와 같다는 것을 유의하여 검산시에 참고해야함!

실제 구현 사항

forward에서는 위상 정렬된 node들을 순차적으로 이동하면서 loss를 알아낸 뒤 backward에서는 위상정렬된 반대방향으로 chain rule을 이용하여 backprop을 진행한다

class ComputationalGraph(object):
	def forward(inputs): # input gate의 input을 넣고 computational graph에 따라 forward 시킴
		for gate in self.graph.nodes_topologically_sorted():
			gate.forward()
		return loss # 마지막 gate에서 나온 최종 loss를 의미
	def backward():
		for gate in reversed(self.graph.nodes_topologically_sorted()):
			gate.backward() # chain rule을 이용한 backprop 진행
		return inputs_gradients	

gate 구현은 다음과 같이 진행한다. forward에서는 단순히 두 값을 곱해주면 되고 backward에서는 dz 즉, 위에서 받은 gradient $\frac{\nabla L}{\nabla z}$ 를 input으로 받아 각각 x와 y에서의 local gradient $\frac{\nabla L}{\nabla x}$와 $\frac{\nabla L}{\nabla y}$를 return하게 만든다. 단, 이때 중요한 것은 $x,y,dx,dy$ 값들을 저장(cache)해야만 나중에 back propagation을 진행할 때 바로 진행할 수 있다.

class MultiplyGate(object):
	def forward(x,y):
		z=x*y
		self.x=x 
		self.y=y
		return z
	def backward(dz):
		dx= self.y* dz
		dy= self.x* dz
		return [dx,dy]

deep learning layer을 구현한 github 코드를 보게 되면 다 이런 식으로 구현하는 것을 알 수 있다.(Caffe layer 소스코드)