구성한 모델을 어떻게 효율적으로 학습시킬까?
이전까지는 data 전처리 방법, weight 초기화 방법, hyperparameter 최적화 방법 등 학습에 필요한 모델을 어떻게 구성할지를 알아봤다. 그렇다면 이렇게 구성한 모델이 역전파를 이용해 어떻게 더 효율적으로 학습을 할 수 있을지 확인해봐야한다. 즉, 이제는 loss가 최소가 되도록 가장 효율적으로 weight 값을 바꿔주는 과정을 알아본다고 생각하면 된다!
Optimization
loss가 최적인 지점을 찾기 위해backpropagation 을 이용하게 되는데 가장 빠르게 최적점에 도달하기 gradient를 이용하여 parameter들을 update하게 된다. 이때 이 어떤 방식으로 gradient를 이용하고 역전파를 활용해야지 최적화하기에 유리한지 알아보고자 한다.
1. Momemtum을 이용하여 최적화
1. SGD(Stochastic Gradient Descent)
기존 값에서 단순히 gradient를 빼서 update하는 것으로 기존에 배웠던 방식과 동일하면서 가장 기본적인 방법이다. CS231n 4-1. Backpropagation (gradient for neural network)SGD 초기에 설정한 learning rate를 이용해 각 차원의 모든 gradient를 합쳐 update의 정도와 방향을 계산하는 방식이다.
🤬문제점
1. 느리다!: 백터들의 합백터가 가장 가파른 방향으로 weight들이 변하게 되는데 이때 딥러닝에서는 높은 차원의 weight들을 사용하기 때문에 연산하는데 걸리는 시간이 많이 걸린다. 또한 zig-zagging 문제가 생길 수 있다. 이 zig-zagging은 각 차원이 loss 공간에 미치는 영향이 다를 때, 즉 경사면의 기울기가 축에 따라 다를 때 나타난다.
y축을 가파른 축, x축을 완만한 축인 loss 공간이 타원형이라고 생각해보자. y축이 가파르다는 뜻은 그만큼 업데이트에서 큰 영향을 받는 것이기 때문에 y축 방향으로 민감하고 크게 움직일 수밖에 없다. 이때 만약 SGD가 아닌 GD(full gradient descent일 경우 y축에서 가장 loss가 작은부분으로 움직인 뒤 x축으로 움직일 것이다. 하지만 실제로 full gradient descent는 매우 비효율적이기 때문에 사용하지 않는다.
SGD에서는 mini batch등을 이용하기 때문에 gradient를 계산하더라도 noise가 생길 수 밖에 없다. 이 noise로 인해 y축에서 가장 작은 부분에서 멈추지 않고 경사면을 더 올라가는 경우가 많으며, 특히 y축으로 매우 민감하기 때문에 작은 noise에도 크게 반응하게 된다. 이때 x축으로 방향으로는 gradient update가 둔하기 때문에 y축 방향으로 왔다갔다하면서 매우 느리게 최적화가 진행되게 된다.
요약하자면, objective function이 각 차원마다 민감한 정도가 다르게 설정이 된다고 한다. 이때 각 차원마다 민감한 정도의 차이가 크게 될 경우 문제가 생길 수 있으며 예를 들어, 아래 그림에서 y축으로 매우 민감하고 x축으로 민감하지 않다면 최적의 값을 찾는데까지 크게 돌아갈 수 있다. 이 문제는 특히 고차원에서 더 커지는데 수십만개의 parameter가 존재하는 deep learning에서는 이러한 차원의 loss에 대한 민감성의 차이가 더 커져 최적화에 오래 걸린다.
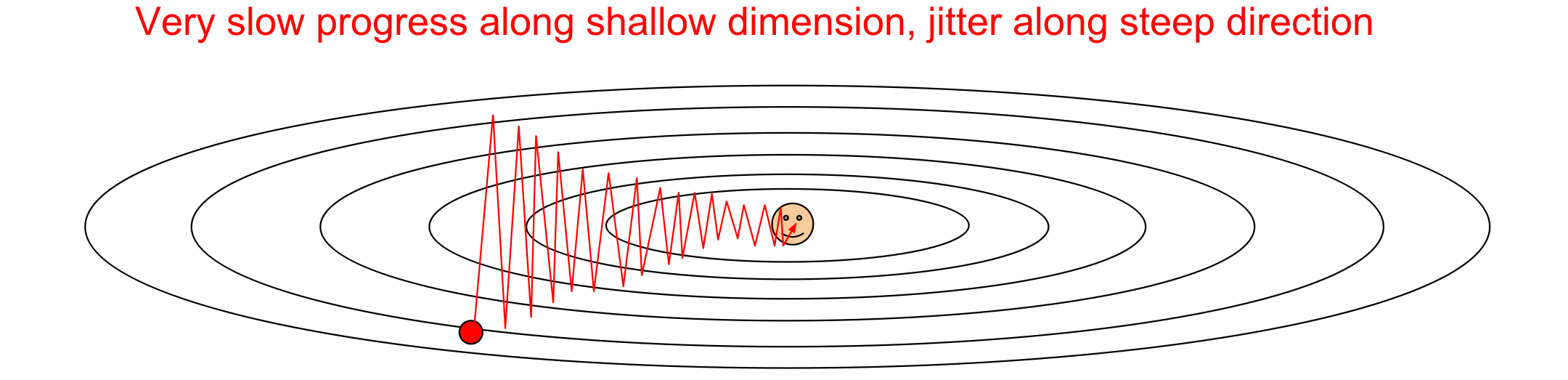
- local minima에서의 문제
loss 공간에 일종의 valley가 존재하는 지역으로 어떠한 지점에서 모든 차원 축에서의 gradient가 0인 상황이다. 이 경우 실제 최적의 값이 존재함에도
SGD가 더 이상 학습을 하지 못하고local optima에 멈추는 문제가 생길 수 있다.
즉, 주위에 기울기가 0일 경우 더 이상 gradient update가 이뤄지지 않는다. 이는 2차원과 같은 저차원에서만 흔히 일어나며 고차원에서는 모든 차원에서의 기울기가 한꺼번에 0이 되는 경우가 매우 드물기 때문에 deep learning에서 크게 문제가 되는 경우가 되지 않는다.
-
Saddle point에서의 문제 여러가지 차원 중 하나의 차원에서 gradient가 0이 될 때를 말하며 이 경우에 이 차원에서의
SGD의 gradient값이 0이 되어 update가 되지 못한다. 고차원을 다루는 deep learning의 특성상 한 지점에서 임의의 차원에서 gradient 값이 0이 되는 경우가 많기 떄문에 실제로는 생각과 다르게saddle point가 문제가 되는 경우가 많다 -
비싼 연산 비용 만약 실제로 모든 input data들을 이용하여 loss를 구해 update하는 경우에는 시간이 매우 오래걸리기 때문에
mini batch를 이용하는데 이럴 경우 실제 값과 달라져 최적의 값까지 가는데 문제가 생길 수 있다. 또한 이 경우 위에서와 같은zig-zagging문제가 나타난다. 이에 더불어mini batch를 사용한다고 하더라도 loss function을 계산할 때 N개의 평균을 이용하여 시간이 오래걸린다는 단점이 존재한다
즉, zig-zagging 문제와 saddle_point 문제를 해결해야할 필요가 있다.
2. Momentum(+SGD)
SGD에서의 local minima, saddle point, zig-zagging등의 문제점을 매우 간단히 해결하였는데 그러기 위해 도입된 개념이 물리에서 속도(velocity)이다.맨 처음 시작하는 위치를 일종의 위치에너지라고 생각하고 이것이 내려가면서 운동에너지로 바뀐다고 생각을 하면 쉬운데, 더 십게 생각하자면 loss 공간에 공을 놓는다고 비유할 수 있다.
차이점
- update되는 요인:
SGD: gradient값 자체가 바로 다음 weight 업데이트에 영향을 주어 다음에 어디로 내려가야할지가 정해진다Momentum: gradient가 일정한 비율만큼 velocity에 영향을 주고 이 velocity를 이용하여 어디로 내려갈지 위치가 정해짐
- step의 방향 및 크기
SGD: 백터들의 gradient 합 방향으로 update가 이루어지고 step의 크기는 떄에 따라 큰 차이가 없음Momentum: velocity의 방향(gradient들이 많이 향하는 방향)이 곧 step의 방향이 되며 velocity가 있기 때문에 step의 크기가 커질 수 있게 된다(속도가 빠를 때는 한번 update될때 많은 step을 내려가게 됨)
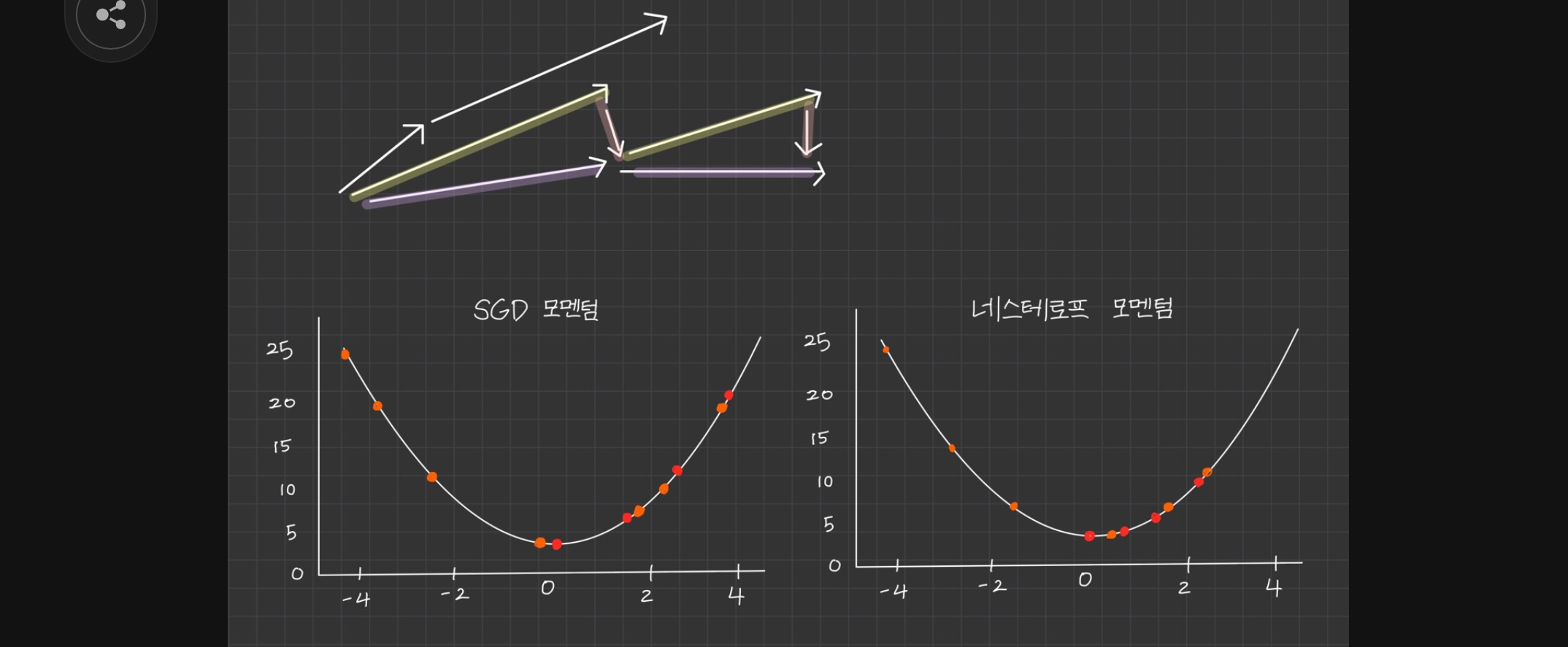
즉, SGD+Momentum 방법에서는 update를 gradient로 하는 것이 아닌 velocity를 이용해 진행한다. 이때 새로운 velocity는 기존의 velocity값에 마찰력을 담당하는 hyperparameter 를 추가해 값을 살짝 줄이고, 여기에 gradient vector항과 합하여 만들어진다. 기존에 optima로 떨어지고 있는 힘 혹은 속도에 gradient 항을 합쳐 기존의 SGD 문제점들을 해결한다. 이때 값은 주로 0.9나 0.99를 사용한다고 한다. 즉 이때 velocity는 지금까지의 gradient들의 weighted sum이라고 볼 수 있다. (최근의 값에 비중 크게, 예전 값에 비중 작게)
계산과정:
- 기존 속도에 friction을 (속도를 늦추는 마찰력이라고 생각)담당하는 momentum(주로 0.9)값을 추가하고 여기에 기존 위치의 gradient를 빼서 예측 속도(v)를 정함
- 이후에 기존의 위치에서 v만큼 이동하게 됨
🤬 문제점?
- 현재 위치에서 gradient로 얼마나 갈지, velocity로 인해 얼마나 갈지를 구한 후 이들의 합백터로 진행한다.
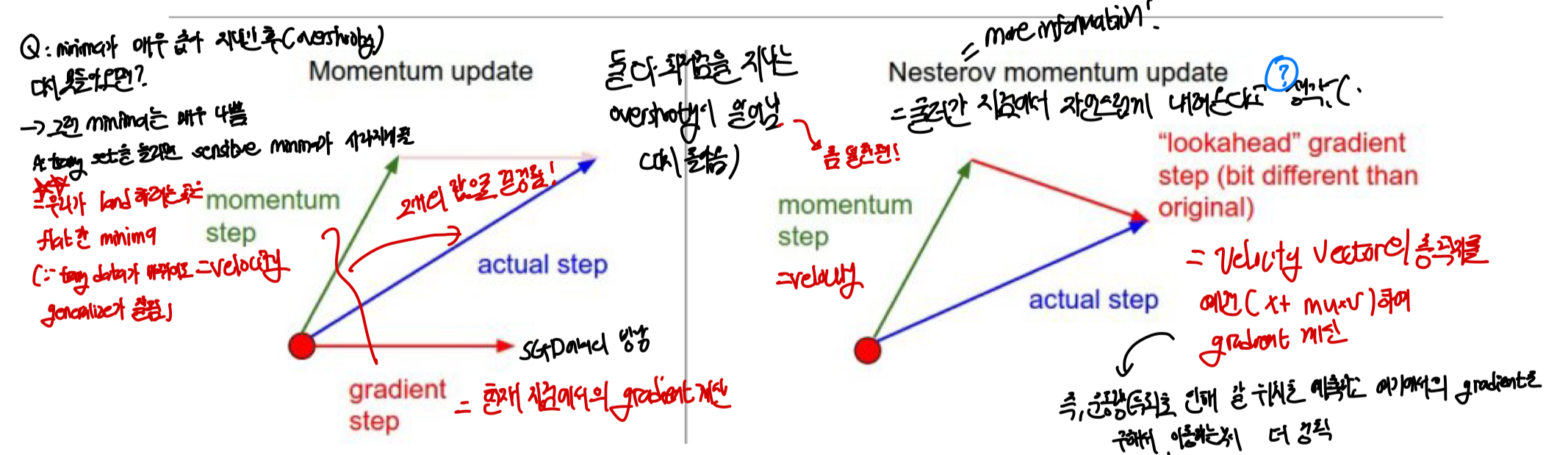
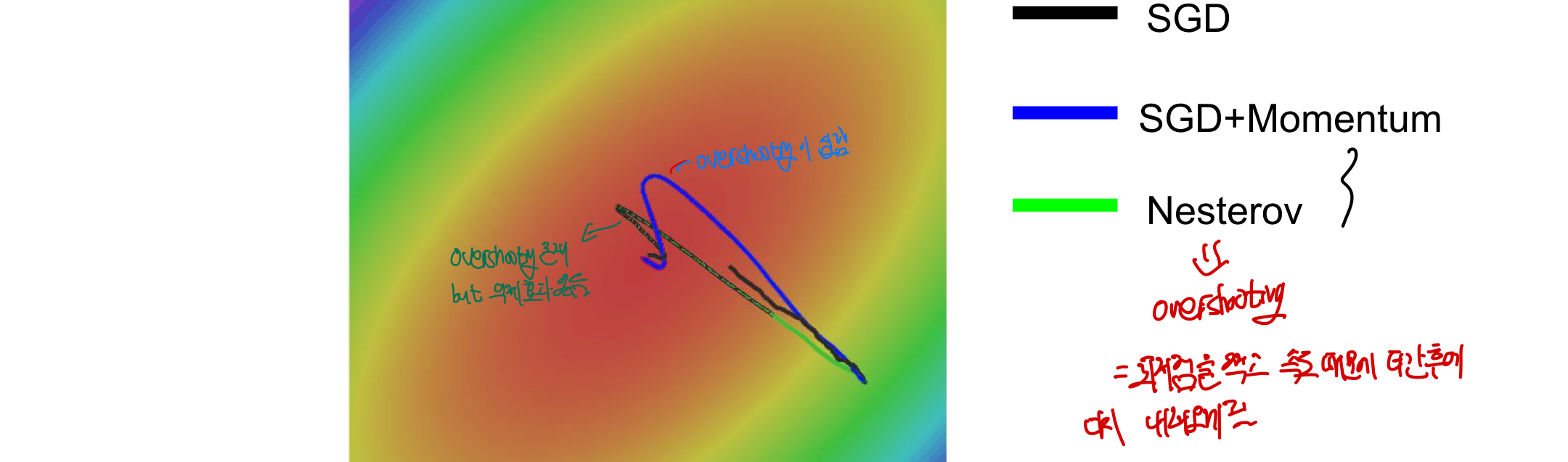
- 속도가 빨라 최적점을 지나가는 overshooting 현상을 억제할 수 없다.

3. Nesterov Momentum
앞서 구한 velocity만큼 이동한 곳에서 gradient를 구하는 방법으로 미래의 정보를 알고 있는 상태에서 가는 update를 진행한다고 생각하면 된다. 주로 convex function(볼록함수)에서 자주 사용된다.
차이점(VS SGD Momentum)
- step의 방향과 크기
Momentum: 현재의 gradient ste + 현재의 velocity step을 합쳐서 합백터값으로 방향이 결정Nesterov: 현재의 velocity step+ velocity step으로 간 곳에서의 gradient 계산한 값이 합쳐져 update가 결정된다. 이때 gradient를 구하는 지점과 velocity를 구하는 지점이 서로 다른 것이 계산에 불편할 수 있는데 이를 식을 변경하여 하나의 지점에서 gradient와 velocity를 구하게 바꿀 수 있다.- 예상 위치 계산: ⇒
- 예상 위치에서의 gradient 계산 및 속도 업데이트: ⇒
- 위치 업데이트: ⇒ …?
- ❓이럴 경우
velocity의 차이가 일종의error term이 되어 update에 역할을 할 수 있다.⇒ 이해가 잘 안된다..!
- overshooting에 정도
Momentum: overshooting 억제 불가Nesterov: overshooting을 막기 위해 한걸음 미리 가보고 overshooting이 될 것 같으면(gradient의 방향이 바뀌어 다시 오르막이 정도가 심해질 경우) 그만큼 직접가지 않도록 만들어 방지한다.
왜 나중에 gradient를 정하는 것이 더 정확할까?
A: 아마 overshooting을 억제할 수 있는 듯! 특히 최적점(
optimal minima)을 지나갔을 때 나아가는 정도가 줄어듦 (gradient와 velocity의 방향이 다를 때 더 빠르게 이 정도를 줄임으로써 overshooting을 억제하는 효과가 나타남)현재 위치에서 기울기를 뺏다가 이게 생각보다 가파르지 않을 수 있으니까 그 다음 위치에서 기울기가 가장 가파른 곳으로 내려가는게 더 합리적(다음 위치의 기울기를 먼저 계산하여 정확히 이용가능)이다. 즉 한발자국 더 빨리 대응이 가능하게 되어
overshooting정도를 줄일 수 있ㄷㅏ.
minima가 매우 좁아 overshooting후 다시 못돌아오면?
A: 우리가 찾고자 하는 곳은 새로운 데이터에도 적용이 가능한 minima이다. 매우 좁은
minima에 경우에는 특정 dataset에서만 나타나는,overfitting을 일으키는 구간일 수 있으며 이러한 곳은 다른 dataset이 들어왔을 때 사라질 가능성이 있다. 이러한 관점에서momentum은 이러한 좁은 minima를 효과적으로 무시하여 지나갈 수 있다는 장점이 존재한다.
 🤬 문제점:
🤬 문제점:
- 현재까지 알아본 optimize 방법들은 모두 learning rate가 고정된 경우(속도 항이 step size를 결정하게 됨)이고 이로 인해 효과적이지 않게 update가 되기도 한다.(step size가 때에 속도나 기울기에 영향을 받지 않고 그 당시에 가장 효과적인만큼 움직일 겨우 더 효율적으로 원하는 최적점에 도착 가능)
- overshooting의 정도는 줄었지만 여전히 존재한다
2. learning rate를 최적화하여 학습
1. AdaFrad
이전에 많이 변화한 parameter는 미래에 적게 변화할거라는 믿음을 가진 방법으로, 각 update마다 얼마만큼의 step으로 움직이는 것이 좋을지 최적화하여 weight를 학습시킨다.
cache: 각 성분이 해당 성분에 대응하는 gradient 제곱값들을 계속 추적(차원마다 추적한다고 생각)
Update 방법
- cache를 이용해 현재까지 각 차원에서 얼마나 많이 변화했는지를 기록하며 gradient가 많이 변화했다면 cache에 해당하는 값이 크게 된다.
- cache값을 분모로 나누어 normalize를 진행한다.
- gradient 크게 변화 → 분모의 값이 커짐→ 변화되는 값 줄어듦 → step 줄어듦→ learning rate가 준 효과
- gradient 적게 변화→ 분모의 값 작아짐→ 변화되는 값 커짐 → step이 커짐 → learning rate가 늘어난 효과
결국 이것은 민감한 차원은 조금만 움직이게 만들고 (큰 gradient 변화→ learning rate 준 효과), 둔한 차원으로는 많이 움직이게 만들어 차원간의 update 속도를 적절히 맞추어 zig-zagging 문제를 velocity 개념 없이 해결이 가능해졌다.
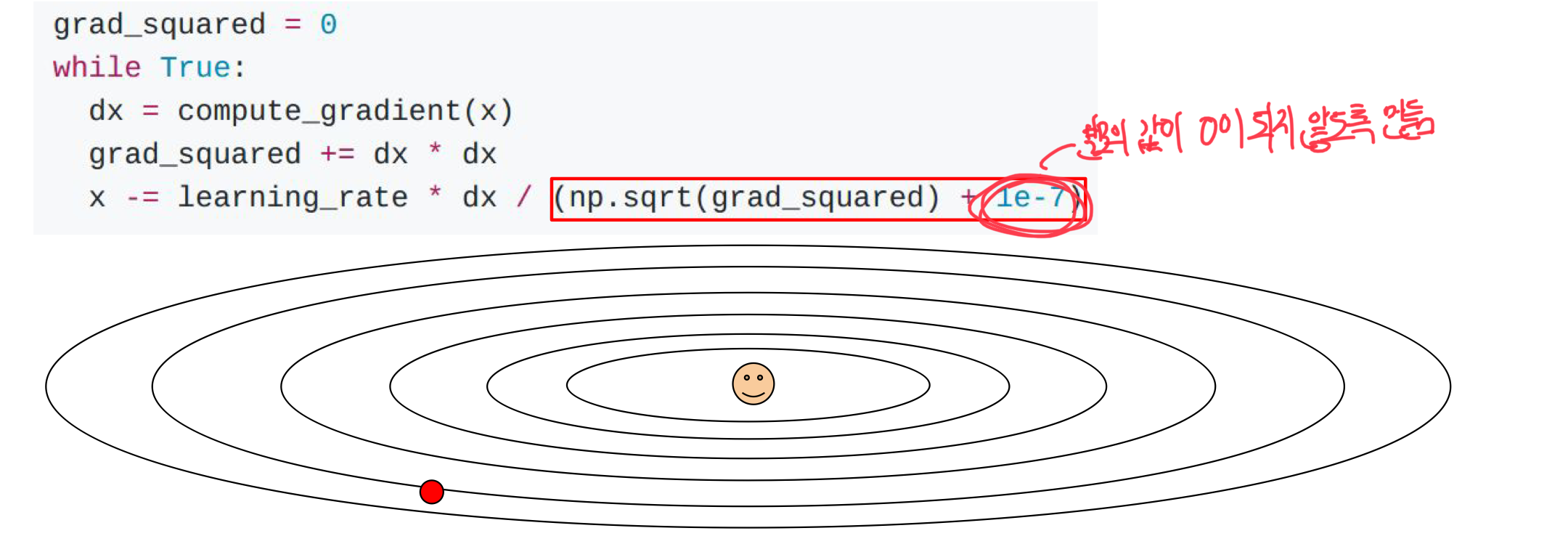
🤬문제점
- stop learning too early
- cache에 gradient값이 갈수록 누적이 되어 learing rate가 매우 크게 감소하게 됨
- learning rate가 0에 수렴하게 되면 더이상 update가 되지 않아 학습이 종료됨
2. RMSprop
RMSprop
learning rate가 0이 되는 것을 decay효과를 이용해 해결하는데 기본적인 개념은 cache를 똑같이 쓰지만 오래된 gradient에 가중치를 낮게 줌으로써 최근의 정보만 사용하게 만든다.
Update 방법
- 기존에 방법과 같이 cache를 구함
- decaying rate를 이용하여 기존 cache와 곱하고 새로 들어온 값은 (1-decay rate)와 곱하여 업데이트
- 지수 평균을 사용하여 과거의 정보를 쓰면서도 최신 값에 큰 가중치를 두어 gradient의 제곱값이 지나치게 증가하는 현상을 완화하여 빠르게 학습이 종료되는 문제를 해결한다.
장점
- learning rate를 변화시킬 수 있음과 동시에 learing이 stop되는 현상을 줄임
- momentum에서 나타났던 overshooting 문제가 해결이 됨(learinig rate를 적절히 조정하여 최적점까지 가는 최단경로와 비슷하게 가게 됨)

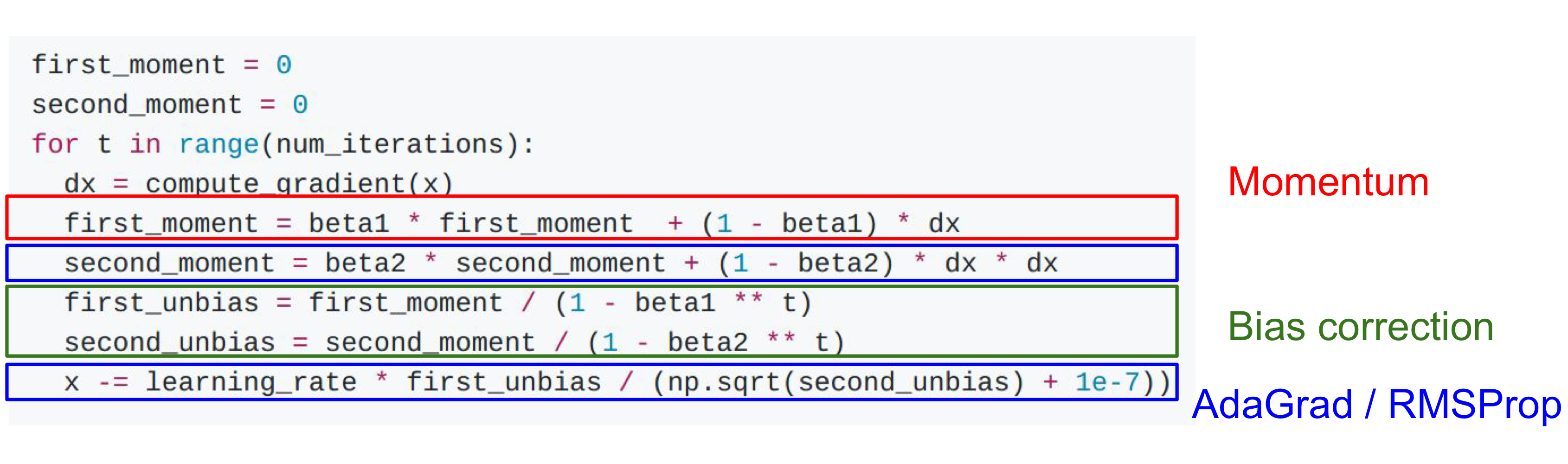
3. Adam
Adam
앞에서 나온 momentum과 RMSProp의 장점을 합친 새로운 방법으로 momentum을 이용해 gradient가 0이어도 넘어가되 너무 빨리 굴러가는 것을 막는다!. 이때 overshooting이 조금 존재하게 된다
Update 방법
- 이동할 크기를 정함 by momentum (후에 learning rate에 의해 나누어져 어디로 얼마나 이동할지 계산이 되며 momentum을 구할 떄도 decay rate가 존재)
- 때에 따라 learning rate를 조절 by RMSProp(
decay_rate를 이용하여 최신 정보 위주로 update) - 실제 이동할 방향과 크기를 계산하여 값을 update by RMSProp&momentum
 🤬 문제점
🤬 문제점
- 초기에는 cache에 값이 0이고 두번째에도 0에 가까운 매우 작은 수이므로 이 수가 분모에 들어가게 되면 learning rate가 매우 커져 처음에 large step을 할 가능성이 있어 수렴에 실패할 수 있다.
- 물론
momentum도 0에 가깝지만 분자(m)에 비해 분모(v)의 scale이 훨씬 작은 경우가 종종 생김
🤩 해결
- bias correction: 초기 학습단게에서 parameter update가 잘 될 수 있도록 만듦
- 작은 값일 때 분모에도 작은값을 넣어 m과 v를 초기화해 첫번째와 두번째 update때 큰 step을 하는 문제를 해결한다

 이
이 Adam의 방식이 유명한 방법이기 때문에 효과적인 hyperparameter 값들이 무엇인지 알려져 있는데, 주로 , , 의 값을 가진다
🤬 문제점..?
- 굳이 문제점을 찾자면 dimension이 기울어져있을때 좌표가(vector) rotate 되지 못하므로 제대로된 경로를 가지지 못하는데 이 문제는 지금까지 알아본 모든 방법에서도 해결이 불가능하다.
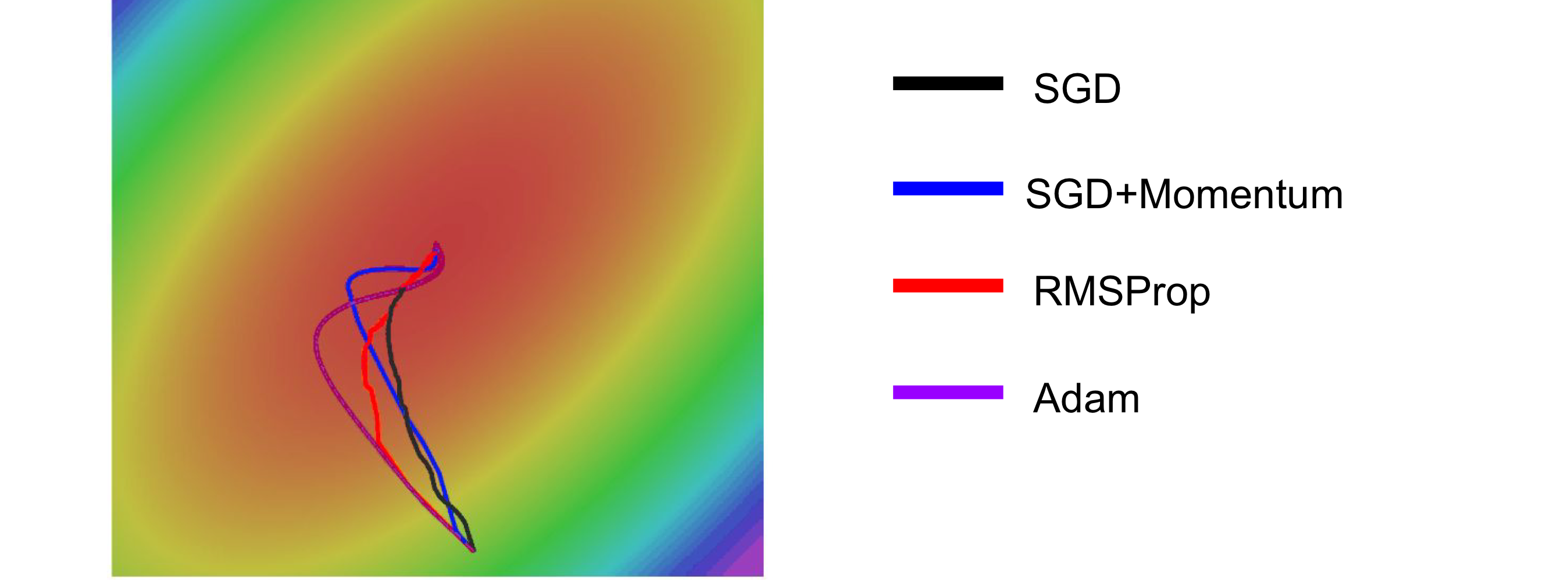
최적의 learning rate는?
앞서 배운 모든 알고리즘(방법)들은 learning rate를 hyperparameter로 갖고 있으며 주로 초기에는 큰 learning rate, 뒤로 갈 수록 learning rate를 낮추는 방법을 주로 사용한다.
- step decay: 특정 epoch마다 일정한 간격으로 learning rate를 감소시킴
- expotential decay, 1/t decay: 특정함 함수를 따라 learning rate를 감소
그런데 이 강의에서는 맨 처음에는 decay하지 않게 하고 나중에 decay가 필요할 때 위의 방법을 사용하라고 추천함
Second order methods(이차근사방법)
특정 지점에서 기존 함수에 근사하는 2차함수를 구하는 것으로 hyperparameter와 learning rate를 구할 필요가 없다는 점에서 장점을 가진다. 하지만 실제 계산에서는 매우 많은 메모리가 필요하고 시간이 오래걸리기 때문에 쓰지 않는다. 자세한 내용은 CS229 3. Logistic RegressionNewton_method 에 정리되어있다
LBFGS: Hessian matrix 방법을 근사한 방법이며 대규모 최적화 문제를 해결하기 위해 고전적인 뉴턴방법을 개선한 알고리즘이다. 가장 큰 특징은 메모리 사용량을 줄였다는 것이다
- 전체 training set을 모두 계산해야함 (mini batch로 하지 않음)
- 가능하다 싶으면 좋은 방법(style transformer에 사용)이지만 주로 사용되지 않음
- 직접 Hessian matrix를 계산하지 않고, 과거의 기울기 정보만을 사용해 근사함