Question
Linear Classification의 문제점
linear classifier은 결국에는 선형적으로 분류할 수 밖에 없다는 특징을 가지고 있는데 (function이 단순한 내적만 존재) Neural network에서는 비선형성도 학습이 가능하다. 이는 모델 중간에 단순한 non-linear layer을 여러개 추가하며 이루어지고 더 복잡한 패턴을 학습할 수 있게 되는데 이는 CS231n 4-1. Backpropagation (gradient for neural network)에서 다뤘던 backpropagation을 통해 여러 layer을 거쳐 parameter들을 학습시키고 loss를 최적화 시킬 수 있기 떄문이다.
기존 classifier의 문제점은 weight W가 곧 하나의 template만을 만든다는 것이었는데 neural network에서 layer가 늘어남에 따라 W가 여러개가 됨으로써 여러 특성들을 반영할 수 있게 된다. 예를 들어 template이 빨간 자동차만을 학습하였다면 기존 classifer에서 노란 자동차를 구별하지 못했는데 더 많은 들이 추가되어서 결국 가장 마지막 에서는 여러가지 색깔의 자동차들도 구별이 가능하다.
이때 추가적인 들은 이전까지의 template의 합인 template이라고 볼 수 있다 ex) template이 왼쪽을 바라보는 말과 오른쪽을 바라보는 말 2개가 있다고 했을 때 x로 왼쪽을 바라보는 말이 들어오게 될 경우 왼쪽을 바라보는 말의 template에서는 높은 점수를 얻게 되고 오른쪽을 바라보는 말에서는 그것보다는 낮은 점수를 얻게 될 것이다. 이것들의 중간 점수 h의 합(weighted sum)을 하여 다음 layer을 통해 또다른 적절한 값의 score을 얻게 되면서 일반화 능력이 커진다
Neural Network 형태 및 구조 by 생물학 비유
앞쪽 layer의 axon에서 보낸 정보()를 synapse(: 고유의 값으로 학습 가능함=synaptic strengths)를 통해 받아 dendrite가 cell body에서 이 정보와 강도를 곱해 () activation function을 거쳐 다음 layer로 이동하며 이때 activation function에는 여러가지가 존재한다
Neural Network 구조에는 크게 fully connected layer과 CNN이 있음
Modeling one Neuron
생물학(뇌)와의 연관성
실제 생물학과의 강력한 연관성은 없지만 이해를 돕기 위한 비유정도로 알아놓으면 좋다
- neuron: like와 dislike를 할 수 있는 능력이 있음
- dendrite: 정보를 받아들이는 역할(수용체)
- synapse: 뉴런들간의 신호가 전달되는 부분 ⇒ 강도와 효율성이 있음
- cell body: 모든 정보를 모음
- axon: 정보를 내보내는 역할
실제 computational 모델
- 앞쪽 layer의 axon에서 보낸 정보()를 synapse(: 고유의 값으로 학습 가능함=synaptic strengths)를 통해 받아 dendrite가 cell body에서 이 정보와 강도를 곱해 () 특정 값을 만들어내게 된다.
- cell body로 오게 된 정보()는 activation_function 의 input이 되어 뉴런의 firing rate 를 반환하게 된다. 이때 cell이 얼마나 firing이 되는지(frequency)만이 모델을 학습하는데 활용이 되는 정보가 된다
- activaition function을 지나고 나온 정보는 다시 axon을 거쳐 다음 neuron, 즉 다음 layer로 넘어감
- [!]
activation function: 비선형함수가 사용되며 입력 신호의 가중치의 합이 input으로 들어와 주로 0~1의 값으로 나오며 1이 될 수록 이 정보(값)을 이용한다고 생각하면 된다. 이때 발화의 빈도에 대해 부호를 해석하여 (시그모이드에서 음수면 가만히 있음)뉴런의 발화빈도를 f로 모델링한다.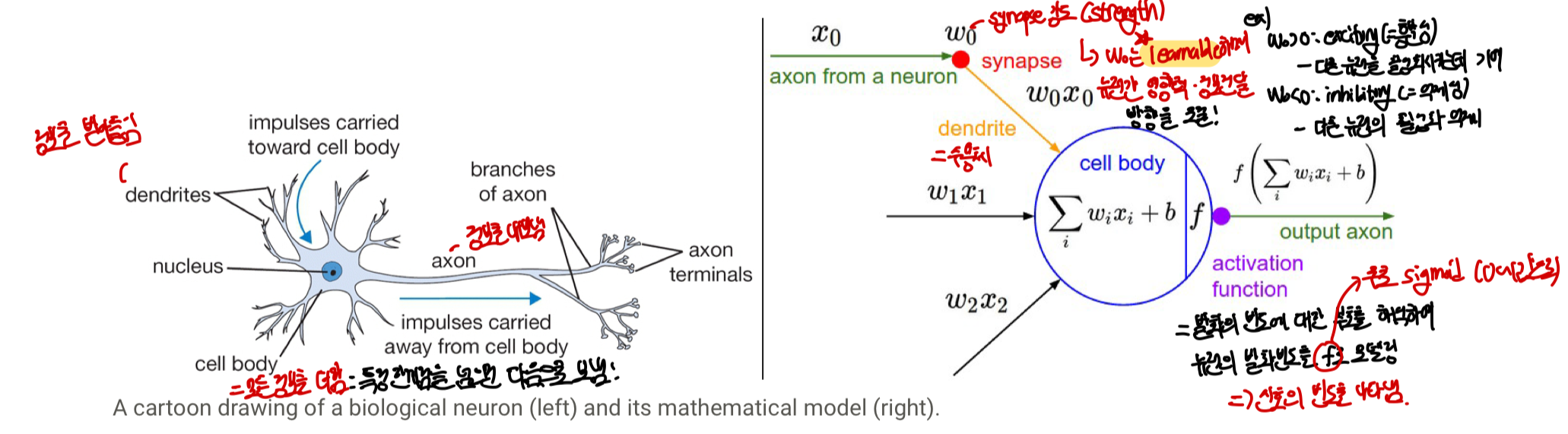 물론 실제뇌는 매우 복잡해서 정밀한 비교를 하기 어려우며 Neuron은 like와 dislike를 할 수 있는 능력이 있기 때문에 각각의 neuron을의 하나의 linear classifier로 볼 수 있다. 즉 하나의 neuron이 Binary Softmax classifier, Binary SVM classifier, Regularization(like, dislike여서 binary인듯)으로 사용이 가능하다는 뜻이다
물론 실제뇌는 매우 복잡해서 정밀한 비교를 하기 어려우며 Neuron은 like와 dislike를 할 수 있는 능력이 있기 때문에 각각의 neuron을의 하나의 linear classifier로 볼 수 있다. 즉 하나의 neuron이 Binary Softmax classifier, Binary SVM classifier, Regularization(like, dislike여서 binary인듯)으로 사용이 가능하다는 뜻이다
간단하게 activation function을 파이썬으로 표현하면 다음과 같으며 이런 식으로 모든 layer의 neuron의 값을 이런식으로 쉽게 계산할 수 있다.
def neuron_tick(inputs):
cell_body_sum=np.sum(inputs*self.weight)+self.bias
firing_rate=1.0/(1.0+math.exp(-cell_body_sum)) # sigmoid function
return firing_rateActivation Function
간단하게는sigmoid 와ReLU function이 존재하며 뒤에 CS231n 6-1. Setting Up Architecture (Activation Functions)에서 더 자세하게 다룬다.
Sigmoid: 모두 정수값을 가지고 값의 범위를 0~1 사이로 압축시킴 (0: 아예 firing 안함, 1: 완전한 firing)
- 단점1. kill gradient: 함수 값이 0과 1에 근사할 경우 gradient가 0의 근사하여 local gradient가 매우 작아지게 되고, 이때 backpropagation을 하면 gradient를 0으로 만들어 제대로 전달이 되지 않을 수 있다.
- 단점 2. not zero-centered: 함수값이 0을 중심으로 있지 않기 때문에(가운데 값이 0.5) 값이 역동적으로 바뀌지 않고 계속 양수값이거나 음수값이 되어 (처음 시작에 모든걸 결정) 학습에 불리하다.
ReLU (Recified Linear Unit):
- 장점 1. 계산속도가 매우 빠르다: 함수가 linear function이기 때문에 gradient를 계산하고 적용하는데 매우 빠름
- 장점 2. 0을 기준으로 한 임계값에 적용이 가능함
- 장점 3.kill gradient 문제 해결: 함수값이 발산하더라도 gradient 값이 일정하여 kill되지 않고 학습이 가능
- 단점 1. 학습 중 gradient가 죽을 수 있음: 함수 값이 음수값을 가지게 되면 gradient가 0이 되어 다시 살아나지 못함
Neural Network architectures
- Fully connected layer acyclic loop로 두개의 인접한 layer의 모든 뉴런들끼리 완전히 연결되어있는 형태이며 단, 같은 layer 내에서는 연결이 되어있지 않다.
- Naming 규칙: input layer은 N-layer에서 N에 들어가지 않으며 총 3가지 layer(input, hidden, output)은 2-layer Neural Network로 불리며
Outer layer은 activation function을 가지고 있지 않고 class score을 나타내는데 사용 된다 - Parameter의 개수=
neuron의 개수 + Weight의 개수 + bias의 개수로 이를 통해 neural network의 크기를 측정함
# 3-layer neural networ의 forward pass
f=lambda x: 1.0/(1.0+np.exp(-x)) # sigmoid acitvation function
x=np.random.randn(3,1) # 3X1 input vector
h1=f(np.dot(W1,x)+b1) # 첫번째 hidden layer activation 계산 (4X1)
h2=f(np.dot(W2,h1)+b2) # (4X1)
out=np.dot(W3,h2)+b3 # output nueron (1X1)