Decision Tree
지금까지 우리가 살펴보았던 ML 알고리즘들과 모델들 (SVM, linear regression..)은 모두 linear model들이었다. 그리고 이번 강의에서 살펴볼decision_tree 는 첫번째로 우리가 다룰 non-linear model이다. 또 후에 배울ensemble 을 적용하기 위한 기초가 되는 부분이 된다.
Decision Tree는 다음과 같은 목표를 가지고 있다. example들이 분포되어있는 feature space를 각각의 region에 들어가도록 만들어 가장 최적된 region을 찾는 것이다. 이 과정에서 3가지 특징을 지니고 있다.
- Greedy: 각각의 split을 하는 step마다 그 당시에 가능한 최선의 partition을 진행한다.
- Top-Down: 하나의 큰 region에서 조금씩 partitioning을 진행해서 쪼개져 나가는 top-down 방식을 취한다.
- Recursive Partitioning: split된 부분에서 또 다시 partitioning을 진행하여 반복한다
Decision Tree의 한가지 예시를 살펴보도록 하자. feature로는 Time(months)와 location(위도)가 있기 ski를 탈 수 있는지 binary classification을 진행하면 밑에 그래프와 같이 example들이 나열이 된다 (+:스키탈 수 있음 -: 스키 못탐). 이때 여러가지 질문들을 통해 점점 region을 나누게 된다.
이런식의 데이터 분포에서는 linear model들로 분리하고 학습하기 쉽지 않다. 물론 SVM 알고리즘과 Kernel을 같이 사용하면 가능하지만, decision tree를 사용하는 것이 훨씬 자연스러운 방법이다.
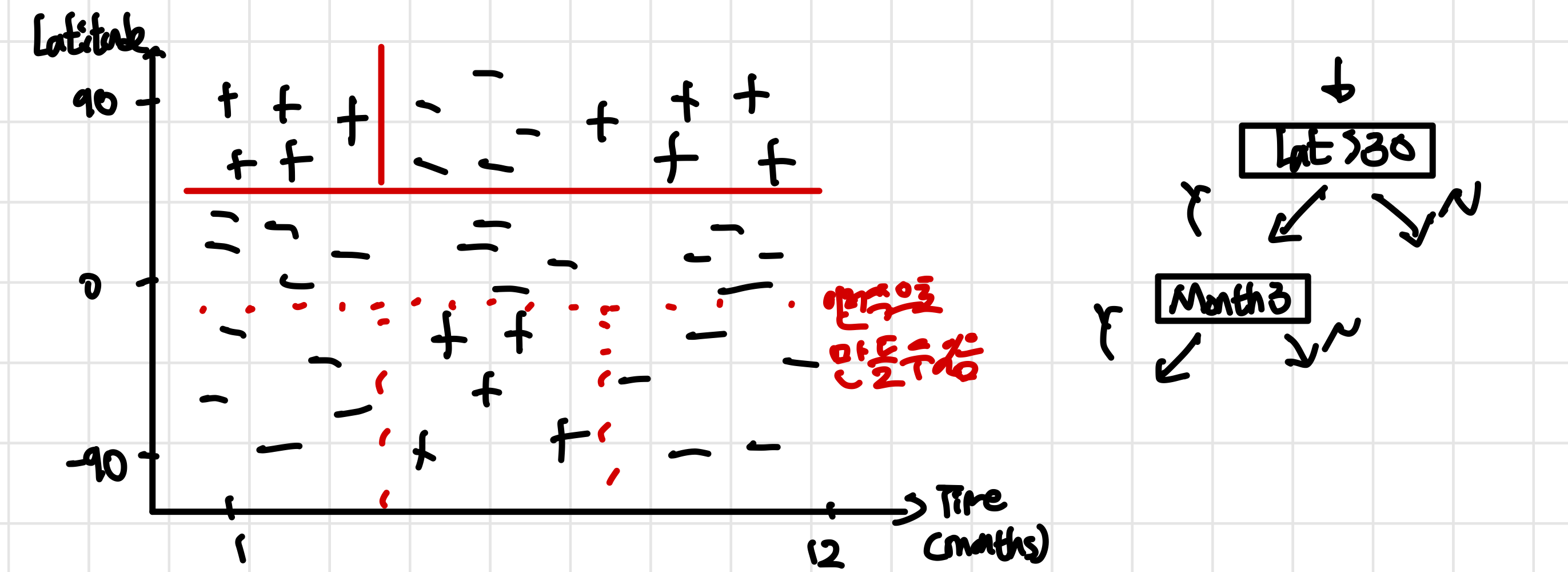그리고 이런 질문들과 도식화 된 그림을 더 수학적으로 표현하기 위해서 split function을 사용한다. 이때 region을 정의하는데 여기서는 상위 region(즉, parent)를 Region 로 하위 region들(즉, 자식)들을 라고 한다. 즉, 로 split이 된 것이다.
이때 우리는 split을 진행하는 split function을 로 정의하고 다음과 같이 표현이 가능하다 $$ \begin{aligned} s_{p}(\overbrace{ j }^{ \text{feature num} }\underbrace{ t }{ \text{threshold} })=&({x\mid x{j}<t,x \in R_{p}},\ &{x\mid x_{j}≥t,x \in R_{p}})\ =&(R_{1},R_{2}) \end{aligned}
즉, 여기서는 j가 feature number(<mark style="background: #ADCCFFA6;">example number?</mark>)이고 t가 split의 경계가 되는 threshold가 된다. parent region 안에 속해있는 example들에 대하여 threshold보다 큰지 작은지에 따라 children region이 정해지게 되는 것이다. ## How to choose splits? --- 그렇다면 부모노드에서 자식노드로 split이 될 때 어떤 split을 해야하고 어떤 split이 좋다고 볼 수 있을까? 그건 바로 **region의 loss**를 통해 알 수 있다. 그리고 여기서는 먼저 #misclassification_loss 에 대해서 알아볼 것이다. 함수들과 parameter들을 정의하면 다음과 같다 - L(R) : Region R에서의 loss - $\hat{p_{c}}$: Class C가 주어졌을 때, Region R안에 있는 example들이 class C에서 차지 하는 비중 - 위 예시에서 class C는 +/-(스키를 탈 수 있다/ 없다)이고 이때 +/-의 비중(비율)을 의미하는게 $\hat{p_{c}}$ $L_{\text{misclass}}=1-max_{c}\hat{p_{c}}$ : misclassifcation한 loss! - 이때 $max_{c}\hat{p}_{c}$를 구하는 것은 **region안에 있는 가장 흔한 class를 예측**하는 것이기 때문이다. 즉, 위 예시에서 북위 30도 이상 3월 이전의 region에서는 +가 -보다 많기 때문에 $\hat{p_{+}}>\hat{p_{-}}$ 가 되어 $max_{c}\hat{p_{c}}=\hat{p_{+}}$가 되며 나머지 $\hat{p}$들에게는 관심을 가지지 않는 것이다. 이런 상황에서 우리는 loss가 가장 많이 줄어드는 split을 원하게 되며, $R\to R_{1},R_{2}$로 split될 때 loss가 최대한 줄어들기를 원한다. 이를 식으로 표현하면 다음과 같이 나타낼 수 있다. $$\max\limits_{j,t}\{\underbrace{ L(R_{p}) }_{ \text{parent loss} }-\underbrace{ (L(R_{1})+L(R_{2})) }_{ \text{children loss} }\}$$ 이때 parent loss $L(R_{_{p}})$는 이미 주어지고 계신되어 있는 값이기 때문에 상수라고 생각하면 되며 여기서 중요한 것은 children loss가 최대한 작아야지만 split했을 때의 값이 최대가 되게 된다. ## Misclassification loss VS Entropy loss --- 하지만 이 *misclassification loss*에도 문제점이 존재한다. 바로 split을 했을 때 성능이 나아지는 것(loss가 줄어드는 것)을 제대로 설명을 하지 못한다. 밑과 같은 예시를 보게 된다면 가장 성능이 좋은 경우는 $R_{p} <R_{1}+R_{2}<R'_{1}+R'_{2}$ 과 같다는 것을 알 수 있다. parent일 때보다 1번의 경우 $R_2$ region에서 200개의 postive 0개의 negative를 가지기 때문에 성능이 더 좋고 loss가 적다는 것을 알 수 있고 2번의 경우에는 $R_{2}$ region에서 500개의 positve, 0개의 negative를 가지기 떄문에 가장 성능이 좋고 loss가 적다는 것을 예상할 수 있다. ![[Pasted image 20240310205953.png]] 하지만 misclassification loss를 살펴보게 되면 이 3가지 경우가 모두 같다는 것을 알 수 있다. 여기서는 틀린 비율이 아니라 틀린 수를 구하고 있다 1. $L(R_{P})=100$ : 100개의 negative가 존재 (postive가 $max \hat{p}$이기 때문에 모든 것을 postivie라고 했을 때 100개의 misclassification이 있다고 새각하면 됨) 2. $L(R_{1})+L(R_{2})=100+0=100$ 3. $L(R'_{1})+L(R'_{2})=100+0=100$ **즉, misclassifcation loss는 sensitive한 loss를 구하는 방식이 아니며 informative하지 않다는 것을 알 수 있다!** ### Cross entropy loss --- #cross-entropy_loss [[KL divergence]]에서도 information theory를 다룸[[18. Mutual Information]]에서도 엔트로피 개념을 다룬다!$$L_{cross}=-\sum_{c}\hat{p_{c}}\log_{2}\hat{p_{c}}$$ 이것이 misclassification 대신에 사용할 수 있는 cross entropy loss의 식으로 information theory와도 밀접하게 관련이 있다. 이때 $\hat{p_{c}}$는 위에서와 같이 region 내의 class의 비율이며, log의 밑이 2인 이유는 cross entropy loss가 정보이론(Information Theory)에서 나왔고 이 정보이론에서 사용하는 단위가 bit이기 때문이다. [[CS231n 2-2. Linear Classification (Loss function)]] 여기서는 information theory의 관점으로 SVM에 사용된 cross-entropy를 설명하고 있다, Cross entropy는 정보이론(Information Theory)에서 두 확률 분포의 차이를 측정하는 지표로 활용이 된다. 그리고 #information_theory 는 **이미 어떤 class에 들어갈지에 대한 확률(분포)을 알고 있는 다른 사람과 소통하거나 얘기할 때 필요한 bits의 수와 관련이 있다고 생각하면 된다.** 예를 들어 누군가 이미 확률을 알고 있을 때 이것이 특정 class라고 100% 확신하고 있다면(region안에 하나의 class밖에 없다면) 그 사람과 소통해서 알려줄 필요가 없어(보내야할 bits가 없음) loss가 작게 된다. 반면에 region안의 class가 동일하게 분포되어 있다면 그 사람에게 많은 정보를줘 어떤 class에 들어가는지 알도록 만들어야하기 때문에(보내야할 bits 많음) loss가 크게 나타난다. >[!important] **Cross entropy & Information theory 요약** > >Cross-entropy는 information theroy에서의 entropy와 관련이 있고 이때 **엔트로피는 어떤 확률 분포의 불확실성을 타나내는 척도로, 더 예측이 가능한 분포는 엔트로피가 낮게 된다** 이때 Cross-entropy는 엔트로피와 모델이 예측한 분포에 대한 엔트로피 기대값을 함께 고려하여 두 분포간의 차이를 측정한다 >결국 cross-entropy의 최소화는 모델이 실제 분포를 정확하게 예측하는 것과 관련이 있으며 classification에서는 loss function으로 사용이 된다 ### Geometric perspective --- miss classification loss와 cross entropy loss 중 어떤 loss가 더 정보적이고 좋은지에 대해서 직관적으로 알 수 있도록 하기 위해 그래프를 통해 설명을 하고자 한다. 이때 binary classification에서 y축은 loss, x축은 $\hat{p_{+}}$라고 가정을 하여 region내 class +에 따른 loss를 나타낸다. 참고로 **이 그래프는 선대칭이 될 수밖에 없는데** +와 -가 동일한 지점에서 loss가 가장 크게 나타난 이후 +의 비중이 그보다 작으면 loss의 값이 $\hat{p_{-}}=1-\hat{p_{+}}$로, 그보다 크면 $\hat{p_{+}}$로 나타내지기 때문에 $\hat{p_{+}}$입장에서 loss의 크기는 대칭적으로 감소하게 된다 ![[Pasted image 20240310220327.png]] 먼저 $R_{1},R_{2}$가 equally weighted(같은 수의 example들을 가지고 있음)하다고 할 때 cross entropy의 그래프를 살펴보면 convex한 형태를 띄게 된다. equally weighted하다면 $R_{p}$에서의 $\hat{p_{+}}$는 $R_{1},R_{2}$에서의 $\hat{p_{+}}$의 평균과 값이 같게 된다. (같은 수의 example들을 가지고 있기 때문에 이 childern의 example들을 합치면 parent에서 class의 비중과 같아져야하기 때문!) 이 경우가 우리가 위에서 본 missclassification이 문제가 되는 부분인데 *cross entropy에서는 $L(R_{p})> \frac{{L(R_{1})+L(R_{2})}}{2}$으로 표현이 되어 일종의 'change in loss'가 발생한다. 즉, parent에서 children region으로 split되면서 loss가 줄어든다는 것*을 알 수 있다. **또한 우리가 가정한 equally weighted하지 않은 경우에도 cross entropy loss function이 볼록하기 때문에 chlidren loss의 두 점으로 이루어진 직선보다 항상 위에 존재한다. 이런 결과로 인해 cross entropy가 더 informative하고 split을 하는게 낫다는 것을 설명가능하다.** >[!question] <mark style="background: #ADCCFFA6;">어떻게 $L(R_{p})> \frac{{L(R_{1})+L(R_{2})}}{2}$가 loss가 줄어든다는 것을 의미하지?</mark> > >$L(R_{p})> \frac{{L(R_{1})+L(R_{2})}}{2}$ 식이 그래프 상에서는 맞는 경우인데 우리가 정의한 loss의 식$$\max\limits_{j,t}\{\underbrace{ L(R_{p}) }_{ \text{parent loss} }-\underbrace{ (L(R_{1})+L(R_{2})) }_{ \text{children loss} }\}$$ 에 넣어보면 값이 음수가 나옴. misclassification의 예시를 넣었을 때는 위 식이 맞는 듯한데, missclassification의 그래프를 봤을 때 이 식이 성립하지 않는다! > >그래서 이 식이 missclassification에서만 쓰는 식인지, 그렇다면 왜 missclassification에 경우에도 성립하지 않는지, loss를 최대한 줄이게 만드는 식은 어떤 것인지 궁금하다. <mark style="background: #ADCCFFA6;">사실 이 식이 평균으로 바뀌어야하는 것은 아닐까?</mark>(사실 그러면 split했을 때 전체 loss는 커지는거니까 더 안좋은건가??, 아마 비중 VS 비율로 확인을 해야할듯) > >**그래프에서는 $\hat{p}$를 proportion 즉, 비중으로 보고 있기 때문에 평균으로 보는 것이 합당하고, 위의 예시에서는 비중이 아닌 수로 확인을 하고 있기 때문에 더하는 것이 합당한듯하다! 그래서 그래프에서는 식을 바꾸어 $$\max\limits_{j,t}\left\{ \underbrace{ L(R_{p}) }_{ \text{parent loss} }-\underbrace{ \frac{{(L(R_{1})+L(R_{2}))}}{2} }_{ \text{average children loss} } \right\}$$이 되어야하는 듯 하다!!** 이번에는 같은 가정하에 missclassification을 보게 된다면 $L(R_{p})= \frac{{L(R_{1})+L(R_{2})}}{2}$가 된다는 것을 알 수 있다. 즉 이 경우에는 region이 split 되었을 때 loss가 줄어든다는 것을 표현하지 못하기 때문에 informative하지 않고 어떤 split이 알 수 없기 때문에 민감(sensitive)하지 않다. 또 다른 decision tree에서 loss function에는 #Geni 가 있는데 $\sum_{c}\hat{p_{c}}(1-\hat{p_{c}})$의 식을 따른다. ($\hat{p_{c}}$에 관한 2차방정식) 대부분의 decision tree의 다른 loss function들은 concave(볼록)하며 $L(R_{p})> \frac{{L(R_{1})+L(R_{2})}}{2}$ 특성을 가져 infromative한 function이 된다. ## Extensions --- 지금까지 살펴본 것은 decision tree가 binary classification에서 어떻게 동작을 하는지였는데, 다른 경우에서도 decision tree가 적용 가능하다는 것을 알아보고자 한다! ![[Pasted image 20240311111235.png]] decision tree를 *regression*에 사용할 수 있다. 위도와 시간에 따라서 강설량이 얼마일지 예측을 해본다면 binary classification에서와 똑같이 각각의 region을 만들고 purity를 늘리도록(특정 class, 값의 분산이 적도록) split을 진행한다. 이때 각 region의 평균을 예측함으로써 regression이 가능하다. 예측하고자 하는 $\hat{y_{m}}$과 loss $L_{\text{squared}}$를 구하면 다음과 같아진다.$$\begin{aligned} \text{Predict: }\hat{y_{m}}=&\frac{\sum\limits_{i \in R_{m}}y_{i}}{\mid\mid R_{m}\mid\mid}\\ L_{\text{squared}}=&\frac{\sum\limits_{i \in R_{m}}(y_{i}-\hat{y_{m}})^2}{\mid\mid R_{m}\mid\mid} \end{aligned}$$ 이때 $\mid\mid R_{m}\mid\mid$은 한 region안에 있는 example의 개수를 의미하며 $L_{\text{squared}}$는 평균에서 얼마나 멀어져있는지를 통해 loss를 구하고 regression을 진행한다. 또한 decision tree는 categorical variable에 도 사용이 가능하다. 위치의 feature가 North/ Equator/ South로 이루어진 categorical variable일 때 '위치가 North에 포함되어 있나요?'라는 질문을 통해 split이 가능해진다. 즉, category의 어느 부분집합으로 들어갔는지 판단하여 split을 진행하는 것이다. 다만 q개의 category가 존재한다면 $2^q$ split이 가능해지기 때문에 category가 너무 많다면 decision tree를 사용하는 것이 좋지 않다. <mark style="background: #ADCCFFA6;">하지만 binary classification에서는 category가 많아도 사용이 가능한데 각 category에 얼마나 많은 positive(class)가 있는지를 확인하여 이것을 linear하게 탐색한 뒤에 최적의 답을 고를 수 있다고 한다.</mark> ## Pros & Cons 결론부터 말하자면 장점과 단점에는 다음과 같이 있다. Pros: - easy to explain (split by question) - Interpertable - Extensions (categroical, regression, classification) - fast Runtime Cons: - High variance -> overfitting - No additive structure - Low predictive accuracy 이렇게 볼 경우 성능면에서 장점보다 단점이 많아 그렇게 도움이 되지 않을 알고리즘이라고 생각할 수 있다. 하지만 맨처음에 얘기했던 것처럼 decision tree 자체가 강력하다기보다는 decision tree에 Ensemble 기법을 넣었을 때 강력해진다. 이 Ensemble 모델을 통해 variance를 줄이고 accuracy를 높일 수 있다 ### Runtime (Pros) --- n개의 example, f개의 feature(가능한 split의 수와 유사), depth가 d라고 했을 때! - **Test time**: *O(d)* -> split을 통해 지나가면 됨 - $d<\log_{2}n$: 어느정도 balanced tree라고 생각했을 때 이 수식이 성립한다. - **Train time:** - *O(d)* nodes: 각각의 point들은 자기자신의 region에 가기까지 d만큼의 시간이 걸린다 - *O(f)* : 각각의 region에서 f개의 split이 가능함! - *O(nfd)* : Total cost!! Train time의 total cost에서 nf는 기존의 matrix와 같은 크기이기 때문에 **사실상 depth d가 runtime에 영향을 주고 이때 $d<\log_{2}n$이기 때문에 굉장히 빠른 runtime을 가지고 있다는 것**을 알 수 있다 ### Regularization (Cons) --- decision tree를 계속하게 진행하게 된다면 각 example 하나가 하나의 region이 되어 overfitting의 문제점을 가지게 된다. 특히, 이런 경우에는 #variance 가 매우 높아지게 된다. **이런 특성 때문에 decision tree는 high variance 모델이라고 불리며, 어디서 split을 멈춰야하는지를 정해야한다!** [[CS229 9. Approx, Estimator Error & ERM]] 1) min leaf size : region안에 있는 data 개수의 하한을 설정 2) maximum depth : tree의 깊이의 상한선을 설정 3) maximum # of nodes : tree의 node(region)의 개수의 상한을 설정 4) minimum decrease in loss : loss가 크게 줄지 않으면 멈추는 방법 - 좋은 방법인 것 처럼 보이지만 **강력한 상관관계를 찾지 못하고 빨리 학습이 끝나 성능이 낮아질 수 있다**. 예를 들어 계속해서 예를 들었던 시간(months)-위치(latitude)와 높은 상관관계를 가지고 있어 같이 사용을 할 때 효과가 매우 커지는 경우가 있다. 하지만 하나의 질문을 통해 split을 했을 때 informative하지 않다고 생각하고 끝날 경우, 그 다음의 질문과 같이 사용했을 때 매우 informative하더라도 끝나게 된다는 문제점을 가진다. 5) #pruning (가지치기): **일단 full tree를 만든 뒤에 되돌아가며 어떤 노드를 없앨지(가지치기)할지 정하는 방법!** - validation set에서 특정 노드를 없앴을 때 misclassification error을 구해 노드의 삭제 여부를 결정하게 된다. 이것이 4)의 문제점을 해결하면서도 regularization을 가할 수 있는 좋은 방법이다 ### No additive structure (Cons) ![[Pasted image 20240311155355.png]] **additive structure이란 모델에서 예측변수 간의 덧셈적인 관계를 가진다는 것을 의미하며 각 요소가 독립적으로 예측에 기여를 한다.** 즉, $Y=f_{1}(x_{1})+f_{2}(x_{2})+\dots+f_{n}(x_{n})+\epsilon$과 같은 관계가 성립하며 logistic regression과 linear regression에서는 쉽게 이 관계를찾을 수 있다. 하지만 decision tree에서는 non-linear 한 특성이 있고, 여러가지 질문을 통해 region을 split 해야만 실제 decision boundary와 근접하게 되기 때문에 additive structure에서 성능이 나쁘다. 또한 decision tree에서는 feature들간의 조합과 상호작용을 고려하지만 additive structure는 각 요소가 독립적으로 예측에 기여하는 경우이기 때문에 이 경우의 decision tree가 알맞는 알고리즘이라고 할 수 없다 # Ensembling decision tree는 바로 위에서도 언급했다싶이 high variance, low accuracy등의 문제점들 때문에 그 자체로 강력하지 않다. 하지만 decision tree에 ensembling을 추가하여 variance를 줄이고 문제점들을 해결해 강력한 알고리즘이 된다. 그 중 먼저 ensembing을 통해 어떻게 variance를 줄이는지 부터 알아보자 ### How to decrease variance --- **Simplistic version** $X_{i}$를 *independent identically distributed(iid)* 한 random variable이라고 가정하면 independent하다는 가정으로 인해 이때 각각의 random variable은 서로 correlate되어 있지 않다. 이런 경우 [[Central Limit Theorem(Gaussian distribution)]] 에 따라 Gaussian을 따르게 되고 random variable의 분산과 표본평균(Sample mean)의 분산을 구하면 다음과 같이 나타나진다 $$Var(X_{i})=\sigma^2\text{ , }Var(\bar{X})=Var\left( \frac{1}{n}\sum_{i}X_{i} \right)=\frac{\sigma^2}{n}$$ 이때 결국 Sample된 X의 variance는 표본(sample)의 개수 n과 밀접한 관련이 있다는 것을 알 수 있다. ($\sigma$는 일종의 결과값이므로 바꾸지 못함). **즉, independent한 경우 variable의 수가 많아지면 많아질 수록 model의 variance는 줄어든다** **General version** 하지만 꼭 random variable x들이 independent한 것은 아니다. 특히 decision tree에서는 X들이 서로 correlate가 되어있기 때문에 independent 가정을 빼고 $X_{i}$들이 identically distributed (id)한다고 하자. 이때 X가 얼마나 correlate되어 있냐를 $p$로 나타낸다면 표본평균의 분산은 다음과 같이 나타낼 수 있다 $$\begin{aligned} Var(\bar{X})=p \sigma^2+&\frac{{1-p}}{n}\sigma^2\\ \text{fully correalte: } Var(\bar{X})&=\sigma^2\\ \text{fully decorrleated: } Var(\bar{X})&=\frac{1}{n}\sigma^2 \end{aligned}$$ fully correlated한 경우에는 $\sigma$=1인 경우로 사실상 모든 variable들이 하나의 variable인 것과 마찬가지이기 떄문에 $Var(\bar{X})=Var(X)=\sigma$가 된다고 생각하면 된다. 반대로 fully decorrelated한 경우에는 independent한 경우이기 때문에 Simplistic version과 같다. 이때 *결국 Variance를 줄이기 위해서는 variable의 수 n을 늘리거나 variable들이 decorrelated($\sigma\to 0$)하게 만들어야 한다* ### Ways to Ensemble --- 그렇다면 이렇게 variance를 줄이기 위해 어떤 방식으로 ensemble을 만들어야할까? 1) different algorithms : 각각의 알고리즘을 설정하기 때문에 시간이 오래걸리지만 kaggle에서 많이 사용 2) different training set: training set을 구하는 것이 쉽지 않고 역시 오래 걸린다 => 1,2번 방법이 성능이 좋지만 시간이 오래걸리는등의 단점이 존재한다 3) Bagging: 서로 다른 training set을 사용하여 근사적으로 학습시키는 방법(완전히 독립적이 아니라 데이터 생성기법으로 통해 다양성 추가) => #randomforest 4) Boosting => AdaBoost, #XGBoost ## Bagging #bagging ensemble의 한 종류로 Bagging을 이용해서 *모델의 variance를 줄일 수 있다* ### Bootstrap Aggergation --- #bootstrap:**통계학에서 추정치(estimate, mean..variance..)의 불확실성(uncertantiy)를 추정하는 방법으로 sample의 복원추출을 통해 sample들을 반복적으로 생성하고, 이를 통해 추출한 sample에서 추정치(estimate)를 계산함으로써 추정치(estimate)의 분포를 근사화하는 방법이다(approximate)** 이를 수학적으로 나타내면 다음과 같다. 실제 분포 $P$를 가지고 있을 때 Training set S는 $S\sim P$를 따른다. 즉, P라는 분포안에 training set S가 존재하다는 것이다. 하지만 ensemble 방법의 2)와 같이 $S_{1},S_{2}\dots S_{n}$을 뽑아 학습시킨다면 시간이 많이 걸리게 된다. **Bootstrap** 그렇기 때문에 $P=S$라고 가정을 한다. 즉, S가 P를 근사하는 것으로 true population을 sample된 값으로 생각하겠다는 것이자 **S에서 복원추출을 통해 Sample을 생성하겠다는 것이다** . Bootstrap sample Z는 $Z \sim S$ 에서 sample을 한다. 이때 Z는 같은 sample S내에 있기 때문에 sample 내에서는 매우 높은 correlation이 존재하게 된다. 이후 모델에 모든 bootstrap sample에 대해 동일한 모델로 학습을 하게 되면,각 모델은 서로 다른 데이터 부분집합(Z)에서 학습이 되어 서로 다른 특성을 학습하게 된다. (불확실성을 추정!) **Aggregate** Bootstrap 하나 자체가 중요하지는 않다. 모든 bootstrap sample들을 모델에 학습시킨 후 평균을 매기는 aggregate과정이 중요하다! 따라서 bootstrap sample들을 $Z_{1},Z_{2},\dots,Z_{m}$라고 하고 $Z_{m}$에 대해서 학습한 모델을 $G_{m}$이라고 한다면 bootstrap 모델은 다음과 같이 나타낼 수 있다. $$G(m)=\frac{\sum_{m}G_{m}(Z)}{M}$$ >[!important] **bootstrap을 이용하면 decorrelation이 일어나는 이유!** > >1. **sampling 변동성** >각각의 sample은 random하게 선택된 데이터로 이루어져있어 sample간에 변동성이 생긴다. >2. **복원 추출** >중복을 허용하는 복원추출은 각 bootstrap sample을 다르게 구성하여 sample내에서는 correlation이 높을 수 있지만 sample간에는 독립성을 부여할 수 있다 > >즉, *중복을 허용하면서 랜덤하게 sample을 추출했을 떄 sample내에서는 correlation이 높을 수는 있지만 sample들 사이에는 서로 다른 구성을 가지기 때문에 decorrelation이 일어나게 된다* ### Bias-Variance Analaysis on Bagging --- 표본평균의 variance가 $Var(\bar{X})=p \sigma^2+\frac{{1-p}}{n}\sigma^2$인 것을 통해 Bagging이 어떻게 variance를 줄이는지 알아보자 1. *Increase n* (random variable의 수를 늘림) bootstrap sample들을 늘리게 되면 variable의 수가 늘어나 n이 증가하고 이로 인해 variace가 줄어든다 2. *decorrelated p* bootstrap을 이용하면 model의 correlated 정도를 줄일 수 있다! 단, 이때 decorrelated 된 p의 lower bound가 존재한다고 한다. (아무리 bootstrap을 진행해도 variance가 0이 될 수는 없음) 또한 bootstrap의 sample들이 증가한다고 하더라도 n이 증가하여 hypothesis 영역은 줄어들고 이로 인해 variance가 줄어 overfit이 일어나지 않는다 [[CS229 9. Approx, Estimator Error & ERM]] 물론 variance가 줄어듦에 따라 bias가 늘어나는 tradeoff가 일어나게 된다! 하지만 decision tree가 high variance 모델이기 때문에 도움이 된다! <mark style="background: #ADCCFFA6;">(random sampling이 일어나게 되면 bias가 줄어들지 않나? 왜 늘어난다고 했지? 그리고 training on less data 때문에 bias가 늘어난다고 했는데 n이 증가하면 결국 더 많은 데이터와 학습하는거 아닌가?</mark>) ## Random Forests --- 지금까지 배운 개념을 통해 random forest 알고리즘과 매우 가까워졌다. Decision tree는 high variance 모델이고 대부분의 error 역시 variance 때문인데 Bagging은 variacne를 줄이는데에 효과적이기 때문이다. (Decision Tree + Bagging ) 하지만 한가지 개념이 더 추가되어야한다. 바로 bootstrap sample로 가능한 $p$(correlate의 정도)의 최저점 보다 더 decorrelate하게 만드는 것이다. 즉 **Random Forest = Decision Tree + Bagging + decrease p** 으로 표현 가능하다. **각각의 split에서, 전체 feature중에 일부분을 고려하여 decorrelate 시키는데** 예를 들어 첫번째 split에서 위치(latitude)만 보고,두번째 split에서는 오직 시간(month)만 확인하는 것이다. 이렇게 되면 각각의 feature들이 최대한 독립적인 것 처럼 보여 p를 줄일 수 있다. 결국 하나씩 다른 feature들과 완전히 decorrelate를 진행시키는 거이다. (*Decrease p + decorrelating Model*) > [!question] **Algorithm VS Random Variable** > > 매우 고차원에서는 알고리즘이 data를 받아 prediction을 output으로 만드는 일종의 classifier로써의 기능을 할 수 있다. 이때 **알고리즘의 output이 특정한 확률적 관점(probabilistic perspective)를 내놓는다면(distribution이 output으로 나올 경우) 알고리즘을 일종의 random variable**로 볼 수 있다. > 즉, Baggining에서와 같이 특정 분포에서 random sample을 할 경우 이를 random variable로 볼 수 있다 ## Boosting --- #Boosting 은 여러개의 약한 학습기(weak learner)들을 결합하여 강한 학습기(strong learner)을 만드는 ensemble의 *bias를 줄이는 알고리즘(근데 variacne를 줄이는게 본 목적이라고 나오긴 gpt가 말해서 bias만 획기적으로 줄이는 것은 아닌듯?)* 이다. Boosting은 Bagging보다 더 additive한 알고리즘으로 하나의 모델을 학습시킨 후에 prediction을 ensemble에 추가를 하는 방식으로 진행이 된다. 이때 이전 학습기(learner)의 오차에 집중하여 새로운 학습기를 훈련시키고, 학습기(learner)의 예측을 가중 평균(weight 존재)하여 최종 예측을 만든다. ![[Pasted image 20240312110208.png]] 위 예시는 오직 하나의 question이 존재하는, 즉 region이 2개밖에 없는 decision tree이며 이떄에 depth가 1인 경우이므로 bias는 크고, variance는 작다. 학습 방법은 일단 +,-의 분포에서 decision boundary를 생성한다. 이때 잘못 예측한 경우(mistake)의 weight를 증가시켜 다음 학습기(learner)에서는 제대로 학습을 할 수 있도록 바꾼다. 이를 반복적으로 진행하여 최적의 decision boundary를 생성한다. 결국 classifier $G_{m}$을 통해 weight $\alpha_{m}$을 결정하여 **높은 가중치를 가지고 있는 모델은 오분류(mistkae)된 sample에 민감하게 반응하여 모델의 성능을 높이기 때문에 더 좋은 모델**이 되며, 가중치(weight)가 적다면 나쁜 모델이라고 볼 수 있다.(이를 반대로 좋은 모델에는 높은 weight를, 나쁜 모델에는 낮은 weight를 준다고 생각할 수 있다) 결국 Boosting에서 classifier은 다음과 같이 정의된다$$G(x)=\sum_{m}\alpha_{m}G_{m}$$ 참고로 #AdaBoost 의 경우 $\log\left( \frac{{1-err_{m}}}{err_{m}} \right)$와 같이 classifier의 성능을 측정한다 >[!important] Boosting이 주로 bias를 줄이는 모델인데도 DT와 같이 쓰이는 이유 > >Decision Tree는 variance가 높기 때문에 이를 줄이는 것이 중요한데 왜 bias를 줄이는 boosting을 사용할까?(오히려 variance가 높아질 수도 있는데!) >1. weak learner의 결합: 여러개의 weak learner를 결합하여 strong learner를 만들경우 **이전 학습기의 error에 집중하여 학습이 되기 때문에 overfitting을 방지하면서 복잡한 패턴을 학습이 가능하다.** >2. 높은 표현력 : decision tree의 비선형 패턴을 잘 학습할 수 있는 능력을 유지하며 높은 표현력 가능하게 만든다 >물론 bias가 줄어드는게 가장 큰 특징이지만 error들을 중점으로 학습을 하게 되면 결국 가능한 hypothesis의 영역이 줄어 오히려 variance가 줄어들 수 있다! >