CS231n 14. Deep Reinforcement Learning

Reinforce algorithm Monte Carlo sampling Actor-Critic Algorithm

What is Reinforcement Learning?

Reinforcement Learning(강화학습): reward를 최대화하기 위해 어떤 action을 취할지 학습하는 과정을 의미 구성요소 - agent: - environment - state - action - reward 동작방식

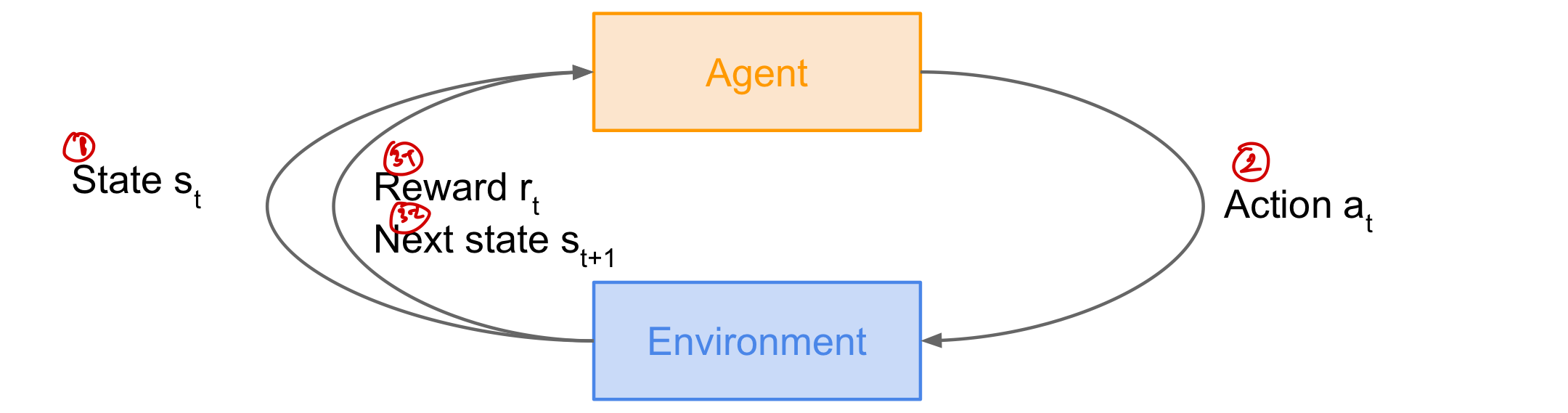
1. environment에서 agent에게 State s_t를 부여
2. agent에 있는 State s_t에서 Action a_t을 하여 environment로 가게 됨
3. environment는 다시 agent에게 Reward r_t와 함께 다음 State s_t+1을 제공
4. 2번과 3번 과정을 반복 Example Cart-Pole Problem(CS229) Robot Locomotion: robot을 앞으로 가게 만드는게 목적(이게 가장 기초적인 방식으로 구현하면 엄청 오래걸리는 예시일거임) Atari Games: 가장 높은 점수로 게임을 끝나는 것을 목적으로 함
   • State: Raw pixel inputs of the game state(action을 통해 pixel이 움직이면서 state 변화)
   • Action: Game control(위,아래,옆..)
   • Reward: 일정한 시간 간격마다 score increase/decrease Go: 게임을 이기는게 목적!
   • State: 모든 pieces(바둑알)의 위치 (바둑판 위에 있는 모든 바둑알의 위치가 곧 state가 됨)
   • Action: 다음 piece(바둑알)을 어디에 놓을지
   • Reward: 게임을 이기면 1, 지면 0

Markov Decision Process

Reinforce 문제들을 수학적으로 표현하기 위해서 MDP(Markov Decision Process)를 사용함! MDP는 Markov property를 만족한다 - Markov property: 다음 상태(state)로의 전이가 현재 상태(state)와 행동(action)에만 의존하며 이전 상태나 행동과는 무관 = 현재 state가 세계의 state를 완전히 나타낸다(미래의 상태는 현재에만 의존, 과거와는 독립!) 구성요소 - S: 가능한 모든 State의 집합 - A: 가능한 모든 Action의 집합 - R: (State,Action) pair가 주어졌을 때 reward의 분포 - P: (State,Action) pair가 주어졌을 때 transition probability(전이 확률)의 분포 - r: discount factor= 최근 reward와 과거 reward간의 차이를 주는 역할 동작방식 by MDP

1. Agent가 Action a_t를 선택한다
2. Environment가 Reward r_t를 sample - r_t~ R(.|s_t,a_t): 현재 State s_t에서 Action a_t를 했을때 (pair가 주어졌을 때) reward의 분포에서 한 reward를 sample!
3. Environment가 next state s_t+1을 sample - s_t+1~ P(.|s_t,a_t): 현재 State s_t에서 Action a_t를 했을때(pair가 주어졌을 때) transition probability의 분포에서 다음 state를 sample
4. Agent가 Reward r_t와 다음 State s_t+1를 받아 위의 과정을 반복

Optimal policy

policy ㅠ: 각 State에서 어떤 Action을 취했는지를 명시해놓은 function 목표: cumulative(sigma:합) discounted(r:감마=할인률), reward(r_t)를 최대화하는 policy ㅠ_star을 찾는 것!! 그럼 우리가 어떻게 RL에서 randomness를 다룰까?(intial state, P:transition probability) = reward의 expected sum을 최대화하는 방향으로 정하면 됨! - policy에 따라 특정 action을 수행했을 떄의 reward를 더한 것이 최대가 되는 policy가 곧 optimal policy

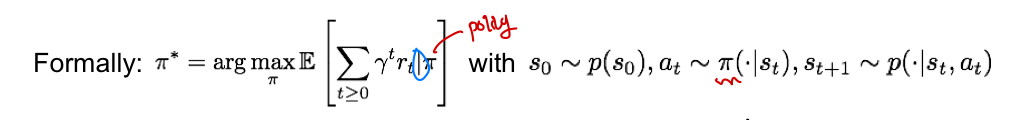
Value function & Q-value function

policy를 따르게 된다면 sample의 자취를 알 수 있음(s_0,a_0,r_0,s_1,a_2..) value function: state가 얼마나 좋을까?= Environment가 state를 고를때! - State s에서 policy ㅠ를 따를 때 기대되는 reward의 총합 - 현재 State에서부터의 reward를 총합을 구해서 얼마나 유망하고 좋은 state인지 확인 Q-value function: state-action pair이 얼마나 좋을까? = Agent가 action을 고를 때 - State s에서 Action a를 하고 policy ㅠ를 따를때 기대되는 reward의 총합 - 특정 state s에서 어떤 action a를 하는 것이 좋은지 확인!

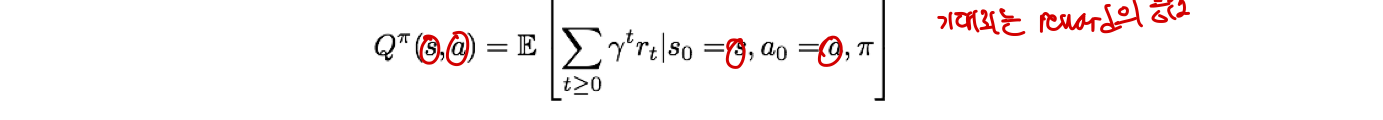
Bellman equation

The optimal Q-value function Q_star는 Bellman equation을 만족한다!! Bellman equation: 다음 state에서의 optimal Q-value function 값에 discount factor r을 곱한 값에 현재 State s에서 Action a를 취했을 때의 reward를 더한 값이 Q_star와 일치한다! - 즉!! 다음 state의 optimal state-action 값 Q_star(s’,a’)를 알고 있다면 optimal strategy는 현재 state에서의 reward를 최대가 되게 만드는 것!! - reward r만 변수가 되게 됨! - 이 bellman equation을 반복하게 된다면 기존 Q-value function을 표현할 수 있음 이렇게 된다면 optimal policy ㅠ_star= 각 state에서 Q_star에 의해 명시된 Action을 계속 취하는 것으로 생각할 수 있음 - maximum future award를 알게 해줌 - 각 state마다 최적의 action을 알게해주는 것이 Q-value function이고 이를 반복한 것이 곧 optimal policy가 됨 - 그럼 value function은 맨 처음 state 구할때만 쓰고 필요가 없는건가? Solving for the optimal policy Value iteration algorithm: 각 iterative update마다 bellman equation을 사용함(이걸 계속 반복한게 곧 Q-value function과 같음) - 아래 식에서 i가 무한대로 갈 경우 Qi가 Q_star로 수렴(converge)되어 Q-value function 알 수 있음! 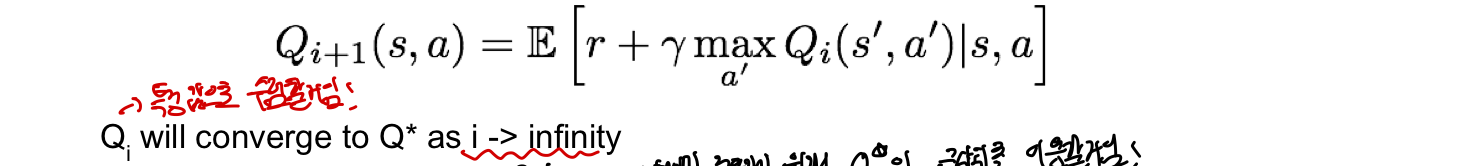문제점: Not scalable함!! - 모든 State-Action pair에 대해 Q(s,a)를 계산해야함 - 모둔 state애 대해서 계산하는 것이 사실상 불가능함! 해결책: Q(s,a)를 평가하는 function approximator를 사용(neural network) - 굉장히 복잡한 function일 때 자주 씀 - GAN과 비슷? non linearity 특성을 사용하여 복잡한 계산을 가능하게?

Q-Learning

Q-learning: action에 대한 가치를 따지는 function(Q-value function)에 대한 function approximator! - 차이점으로는 parameter theta가 있어 이 값에 의해 전체 값이 정해지게 됨! - 만약 function approximator가 deep neural network라면 deep q-learning이라고 불림! 그래도 여전히 우리는 Bellman Equation을 만족시키는 Q-value function을 찾고 싶은거임! (다만 forward와 backward pass에서 계산하는 것이 불가능) - function Q를 학습시켜 bellman equation을 만족시키는 Q-function과 유사하게 만들고 이를 통해 간편하게 forward, backward pass를 진행! Forward Pass: y(target value)는 Bellman Equation을 통해 구한 Q-function값이 되며 이 값이 기준이 됨 - 이 값을 기준으로 Loss function을 만들어 loss를 구하게 만듦 Backward Pass: Q-function의 parameter theta에 대해 update 진행

Q-network Architecture

Q-learning는 결국 neural network를 사용하여 parameter theta를 업데이틑 시켜 Q-value function과 유사하게 만드는 것을 목적으로 하는데 그렇다면 이 neural network는 어떤 형태일까? Q(s,a,theta) neural network: parameter theta를 weight로 사용 - Atari Game을 예시로 듦

1. input: State s_t가 들어감
2. Conv & FC layer: input state가 layer을 거쳐가며 feature로 표현하게 됨
3. Last FC layer: 4개의 output(action)으로 구성되며 이는 각각 Q-value값을 나타냄 - 해당 action을 하게 될 경우 얼마나 많은 reward를 가지게 될지 - 다음은 어떤 action을 취할지 정하는 기준이 됨 Neural Network를 통해 학습하면서 더 정확한 Q-value값을 얻게 되어 이를 통해 다음에는 어떤 action을 취해 전체 reward를 높일 수 있게 만듦 장점: 현재의 state에서 모든 Q-value들을 한번의 forward pass를 통해 구할 수 있음!
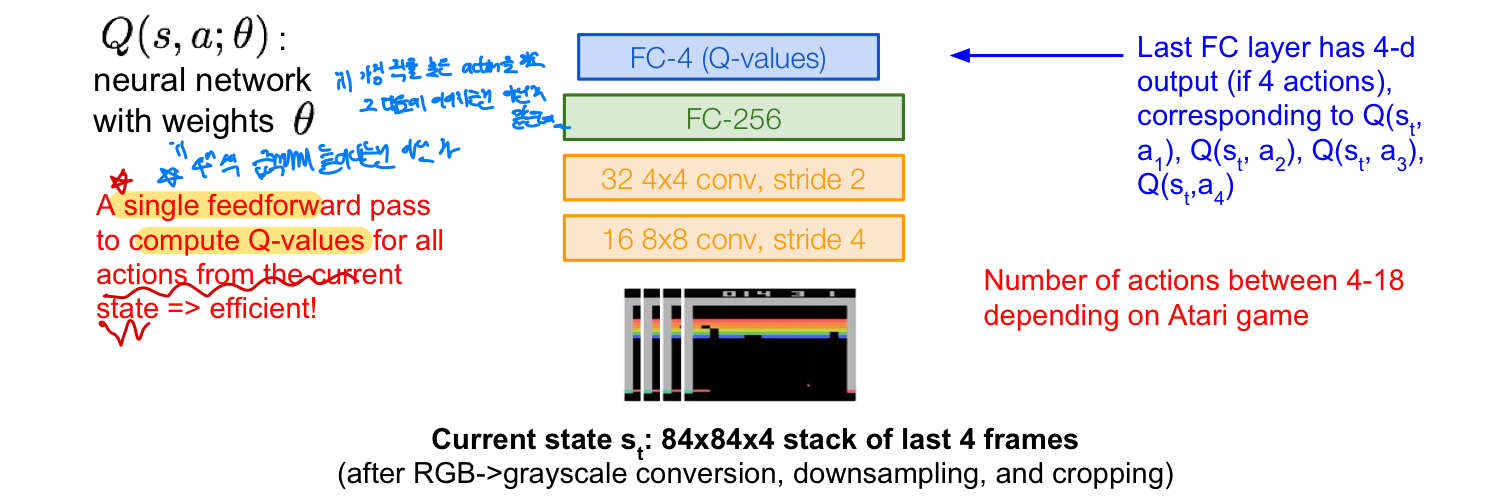
   • neural network를 통해 복잡한 Q-value값들을 계산할 수 있도록 modeling해서 가능한 일!!

Experience Replay

Q-network의 문제점 연속적인 sample들의 bach로 학습할 경우 문제가 생김 - Correlated sample - training은 sample들이 서로 독립적이어야 효율적임 - 앞선 게임처럼 일련의 지속적인 action을 통한 training은 모두 연결되어 있어 비효율적 - Q-network parameter는 다음 training sample에 영향을 받을 수 밖에 없는데 이것이 bad feedback loop로 이어질 수 있음 - 연속적으로 되어있다면 처음에 한쪽으로 치우치게 되면 계속 한쪽으로 치우져 제대로 update가 되지 못함함 해결책: Experience Replay - transition(s_t, a_t, r_t, s_t+1)을 replay memory table에 저장하고 이를 꾸준히 update - 연속적인 sample들을 쓰는 대신에 replay memory로부터 transition의 batch를 random하게 골라 Q-network를 train - 각각의 transition은 weight update에 여러번 기여할 수 있음 - replay memory table에서부터 sampling하면 하나의 sample도 여러번 뽑힐 수 있음! - data efficiency!! 알고리즘 기 Poolicy에 따라 action을 어떻게 뽑을지 정한다 Action을 통해 정해진 State등의 정보를 transition에 넣고 이 transition을 replay memeory에 저장한다. 이후 이 replay memory에서 무작위로 sample하여 Loss를 구하여 gradient descent를 진행하고 다시 이 state에서 action을 고르는 것을 반복! - 이때 다시 action을 고를 때 replay memory에서 sample한 state에서 진행하는지 아니면 그전에 action으로 가게 된 state s_t+1에서 진행되는지? 문제점: experience replay로 문제를 어느정도 해결하더라도 Q-function 자체가 매우 복잡하여 문제가 있음 - ex) 로봇이 물체를 잡는 것은 매우 고차원의 state가 필요함 - 각각의 (State,Action) pair을 정확히 학습하는 것이 어려움 - 하지만 더 간단하게 하는 방법이 있음(그냥 손을 잡으라고 학습시키는 것!) ⇒ directly learn a policy!! (Finding the best policy!)

Policy Gradient

앞선 Q-Learning에서 Q-function 자체가 너무 복잡하다는 단점을 보완하여 단순히 policy를 학습시키자! - 지금까지는 각 action들에 대해서 모두 계산을 했다면 이제는 policy 그 자체를 학습시킴 - 우리는 optimal policy를 구하고 싶음!(지금까지도 계속 optimal policy를 찾는 과정이었음) - optimal policy theta_star=argmax(J(theta)) - policy parameter에 대해 gradient ascent를 진행하여 parameter을 향상사키기고 reward의 총합을 증가시킨다! - policy ㅠ: 각 State에서 어떤 Action을 취했는지를 명시해놓은 function

Expected reward

trajectory(흔적): 특정 policy theta가 정해지면 state,action,reward가 나온 것을 의미 - object function은 이 trajectory를 기반으로 reward를 측정 object function은 기댓값의 합으로 구성이 되는데, 보통 기댓값 = (확률) X (그 확률일때의 값) 이 된다! - 기댓값 = (특정 policy일때 (state,action) pair일 확률) X (reward의 값)

policy reward J(theta)= 우리의 policy(특정 trajectory일 확률을 theta에 대한 확률 분포로 나타낸 곳)에서의 sample한 trajectory에 그때의 reward를 곱해 모든 trajectory에 대해 더한 값 = expected future reward over trajectory! = (value of policy) X (reward of trajectory)

확률 표현식

p(r;k): r이라는 변수가 특정 값일 확률을 k에 대한 확률 분포로 나타내는 것! p(.): 주로 확률 분포를 나타내는 함수 & 세미콜론(;) 뒤에 오는 것은 해당 분포의 매개변수를 의미 p(x;u,a): 평균이 u이고 표준편차가 a이 확률분포를 의미!

Differentiate (Gradient)

Expected reward에 대한 식을 알았으니 이제 gradient ascent를 이용하여 parameter theta를 update하여 optimal policy를 구해야함! - theta에 대해 미분하려고 하지만 이 식은 intractable함 - p가 theta에 대한 분포를 따르기 때문에 결국 theta에 종속되어 있는데, 이것 자체를 미분하기도 어려울 뿐더러 이를 다시 r에 대한 적분을 하기 어려워 intractable함! 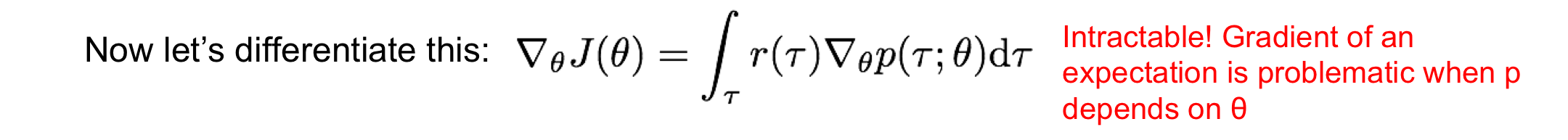Nice Trick: gradient log(f)=gradient log(f)/ f 인 log의 도함수 성질을 이용! - 이후 chat gpt가 알려준 기댓값의 식을 통해 다시 gradient를 구할 수 있는 식으로 만들 수 있음 - expectation의 gradient를 transform시켜 gradient의 expectation을 구하게 바꾸어 계산가능도록! - 그렇다면 이 바꾼 식에서 어떻게 평균을 구해 gradient를 구할 수 있을까? 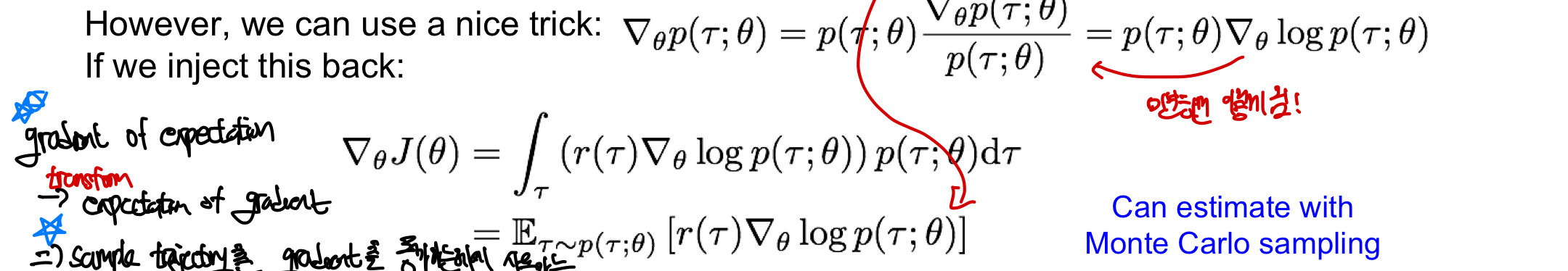Monte Carlo Sampling을 통해 근사해 gradient 값을 알 수 있다!! #Monte_Carlo sampling: 확률적인 방법을 사용하여 수치적 적분이나 예상값을 추정하는 방법! - 여기서는 Expected reward의 gradient 값을 확률적인 방법을 사용하여 예상 값을 추정하는 방법을 사용(특히 평균ㅇ나 적분 값 추정에 많이 사용) 1. Sampling(표본추출): 특정 영역에서 무작위로 표본 추출(난수를 사용) 2. 함수 값 계산: 각 표본에 대해 함수 값을 계산 3. 평균추정: 계산된 함수값의 평균을 이용하여 원하는 값의 추정치를 얻음(표본의 수가 증가→추정치가 실제 값에 수렴) 이 Monte Carlo sampling을 이용하여 transition probability를 알고 있지 않더라 값을 구할 수 있다

1. probability of trajectory=trajectory의 모든 state와 action이 실행될 확률의 곱으로 나타낼 수 있음 - [transition probability(특정 state로 갈 확률)] X [policy ㅠ로부터 받은action이 실행될 확률]의 곱의 반복 - 이를 모두 곱하면 trajectory(경로)에 대한 확률을 얻어낼 수 있음
2. 이 식을 log로 나타냄 - log로 나타낼 경우 log의 성질에 의해 곱셈이 덧셈으로 표현 가능해짐 - log를 씌우는 이유는 우리가 구하고자 하는 식의 형태에 log가 들어가 있음!
3. theta에 대해 미분 진행 - theta에 대해 미분을 진행하기 때문에 theta가 없는(theta입장에서 상수) transition probability가 없어짐 - single expression으로 표현이 가능해짐 trajectory r(tau)를 sampling할때 expected reward J(theta)를 monte_carlo를 이용한 gradient 근사를 통해 구할 수 있게 됨! 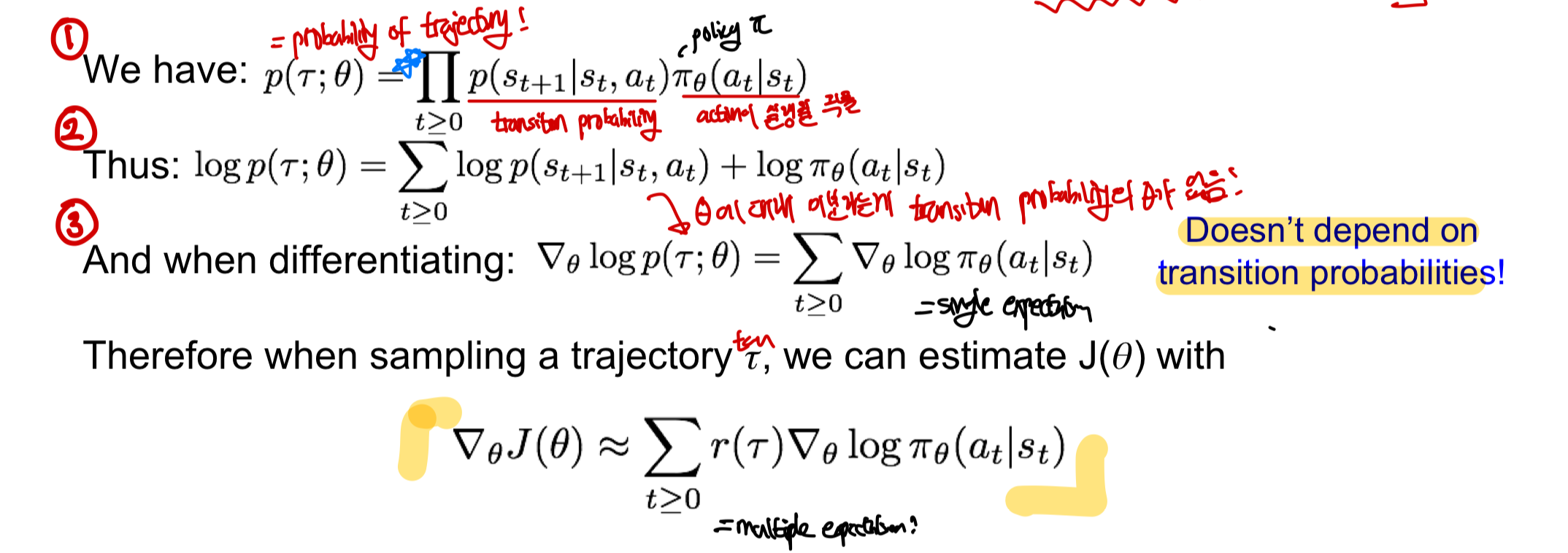Intuition
4. 결국 theta에 대해서 미분을 진행하기 때문에 gradient를 구해 action이 뽑힐 확률을 바꾸게 됨 - ㅠ_theta(a_t |s_t)= policy ㅠ로부터 받은 action이 실행될 확률
5. reward만큼 scale을 통해 Expeceted reward J(theta)값을 바꾸게 됨 - r(r), sequence of action의 reward가 좋다고 하면 이와 관련된 action이 많이 뽑히도록 확률을 올림 - 반대로 값이 낮으면 (reward가 적으면) 이와 관련된 action이 조금만 뽑히도록 확률을 줄임 결과적으로 정리해보면 trajectory의 reward가 좋다면 이와 관련된 모든 action들이 좋다고 판단할 수 있음 - action들의 reward 평균이 곧 trajectory의 성능을 결정 - 충분히 많은 sampling을 통해 시행횟수를 늘리면 최적화가 가능하기는 하지만… credit assingment(신뢰 할당 문제)가 매우 어려움 → high variance 문제를 가짐! - 일단 보상을 받았으면 해당 trajectory의 모든 action이 좋았다는 정보만 알 수 있음 - 하지만 구체적으로 어떤 action이 좋인지 알 수 없고 모두 성능이 좋은 action이 아닐 수 있음 - high variance = 좋은 reward의 분포가 한쪽에 모여있지 않고 떨어져 있음

Variance Reduction

기존의 방법은 variance가 크다는 것이 문제인데 이 variance를 줄이는 것이 중요함(by sampling을 적게하면서도 estimator의 성능을 높이는 방법)

1. 현재의 State으로부터 받을 미래의 Reward만을 고려하여 어떤 Action의 확률을 올려주는 것 - 해당 trajectory에서 얻을 수 있는 전체 Reward 대신에 현재의 time step에서 종료시까지 얻는 reward만 고려
2. delayed effect에 대해 discount factor을 사용하여 무시 - discount factor을 추가하여 가까운 미래에 더 많은 비중을 부여 - 먼 미래에는 더 적은 비중의 reward를 부여하여 가중치에서의 차이를 토대로 estimator의 성능을 높임
3. Baseline!!!!

Baseline

trajectory 자체에서 구한 값이 반드시 의미 있는 것은 아님!(계산한 값을 그대로 사용하는 것이 문제일 수 있음) - reward가 모두 양수인 경우 action에 대한 확률이 점점 올라갈거임 예상했던 것보다 reward가 클지 작을지가 중요함! - baseline function을 사용하여 해당 state에서 우리가 얼마만큼의 reward를 원하는지를 계산 가능 - 즉, reward가 좋은지 안좋은지를 구분해주는 기준이 됨! 그럼 baseline을 어떻게 뽑아?

1. 지금까지의 평균을 기준 - 지금까지의 평균이 baseline이 되어 계산한 reward가 좋은지 안좋은지 판단하는 기준이 됨 - 다음 state로 진행되게 되면서 지금까지의 평균이 바뀌고, baseline도 변화하게 됨
2. Q-function과 value function을 이용 - 어떤 Action이 그 State에서의 기댓값보다 좋은 경우에 그 Action을 하려고 할 것! - Q-function: (State,Action)이 얼마나 좋을지 판단하는 함수로 future reward를 계산할 수 있음 - 즉, 실제 계산한 값이라고 할 수 있음 - value function : 현재 state가 얼마나 좋은지 판단하는 함수로 State에서의 기댓값을 계산 가능 - 즉, 기댓값이 기준이 되는 baseline function이라고 할 수 있음 Q-function과 value function을 통해 얼마나 scaling할지(일종의 scaling factor) 정할 수 있음! 즉, 현재의 Action이 얼마 좋은 행동이었는지 알 수 있게 되었으며 이를 통해 gradient를 구해 더 정확한 학습과 최적화가 가능해지게 됨!

Actor-Critic Algorithm

지금 위에서 구한 Q-function과 value function을 따로 구하지는 않았지만 학습은 시킬 수 있는 방법! - by Q-learning - 앞서 배운 Policy Gradient와 Q-learning을 합쳐서 학습이 가능 - actor=policy, critic=Q-function: 어떤 State가 얼마나 좋았는지 & 어떤 Action이 얼마나 좋았는지! 알고리즘 구성 1. actor(policy)가 어떤 Action을 취할지 정하고, critic(Q)가 actor(policy)에게 이게 얼마나 좋은 Action이었고 어떻게 조절해야하는지를 알려줌 2. critic(Q)는 오직 actor(policy)가 만들어낸 (state,action) pair에 대해서만 학습을 시키면 됨! - 기존의 Q-learning은 모든 (State,Action) pair에 대해서 학습을 했었음 - Q-learning의 일이 줄어들었기 때문에 이를 ‘alleviate’(완화) 되었다고 표현 3. experience replay와 같은 Q-learning의 전략들도 추가 가능 결국 advantage function은 어떠한 Action이 예상보다 얼마나 더 괜찮았는지를 결정하는 함수! - advantage function은 Q(s,a)-V(s)로 표현 가능(위에서와 같음) policy function과 critic function을 반복적으로 학습시키고 gradient를 update하면서 학습 진행 알고리즘 과정 1. Policy parameter theta와 critic paramter phi를 초기화해줌 2. 매 학습마다 현재 policy를 기반으로 m개의 trajectory(경로)를 sampling 3. Gradient를 계산하소 각 trajectory마다 advantage function A_t를 게산 4. 이 advantage function을 이용해서 gradient estimator을 계산하고 누적시킴 5. advantage function를 최소화시켜 value function를 학습시키고 이걸로 ㅠ를 학습시킴 ⇒ 이 과정을 통해 policy와 critic function을 반복적으로 학습시키고 gradient를 update!

RAM(Recurrent Attention Model)

Reninforce를 실제로 사용한 예이며 Image Classification을 목적으로 함 이미지의 전체가 아닌 지역적인 부분만을 순차적으로 glimpse하면서 class를 예측하는 방법! - 이런 방식은 인간이 보는 방법과 비슷하게 작용하도록 만들었음 by 사람의 인지 & 안구운동 - computational 자원을 아낄 수 있음 - low resolution(저해상도)로 각 부분을 지역적으로 살펴보고 고해상도로 세부적인 것을 살펴봄 - 이미지 전체를 처리할 필요가 없기 때문에 크기가 큰 이미지에 효과적 - 이미지의 중요하지 않은 부분을 무시할 수 있음 → classification 성능을 높임 - 즉, 내가 원하는 부분만 학습이 가능하여 ConvnNet에 처리하려는 부분만 선택 가능 이러한 “Glimpsing”은 미분 불가능한 연산 ⇒ Reinforce를 이용하여 glimpse Action에 대한 policy를 통해 학습 가능해짐!! 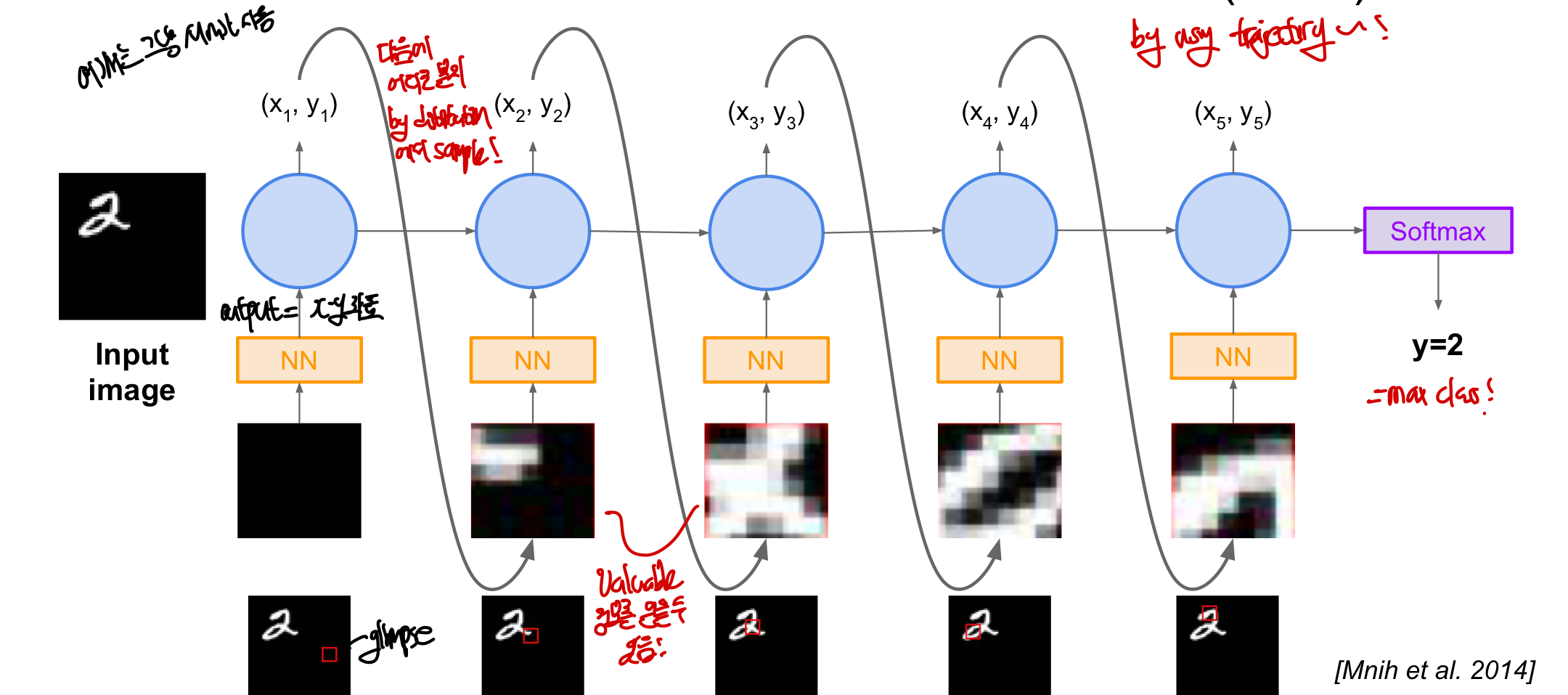- 누적된 glimpse가 주어졌을때 State를 모델링하기 위해 RNN 이용 - State: 지금까지 관찰한 glimpse - Action: image 내에서 어떤 부분을 볼지 선택하는 것(좌표를 선택!) - Reward: image가 제대로 classify된다면 1점을 얻음 동작과정 1. 사진에서 무작위로 한 부분을 잡고 Neural Network를 통과함 2. Neural Network의 결과로 (x,y)좌표가 나오게 되는데 이는, Action에 대한 distribution 형태! - 주로 Gaussian을 따르며, output이 곧 distribution의 평균이 됨! - RNN을 이용하기 때문에 지금까지 있었던 모든 glimpse를 전부 결합시켜야 함 3. 이 distribution에서 특정 x,y위치를 sampling하여 다음 glimpse를 얻어냄 4. 위 과정을 반복 5. 마지막 time step에는 softmax를 통해 각 class의 확률 분포를 출력하여 max class를 output! gradient를 구하는 것은 앞서 배운 reinforce 알고리즘을 통해 모델과 policy parameter들을 학습 가능! - 계산 효율이 좋고 image내 불필요한 정보 무시 가능 - image captioning, visual question-answering task들에 사용

AlphaGo

supervised learning과 reinforcement learning을 혼합하여 학습을 진행! - Action: 새로운 바둑알을 좌표(바둑판) 올리는 것 - State: 바둑판 위에 있는 모든 점 - Reward: 경기를 이길 경우 1 알고리즘 동작과정 1. 입력 백터 생성 & feature board - 바둑판, 바둑돌의 위치들을 특징화 시켜 입력이 될 수 있도록 만듦 - 바둑돌의 색깔, bias와 같은 채널들을 추가하여 바둑의 형세를 표현! 2. 프로 바둑시가의 지도를 supervised learning으로 학습시켜 network를 초기화 - 바둑판의 현재 State가 주어졌을 때 어떤 Action을 취할지를 정함 - 프로 바둑기사의 기보가 주어지면 바둑기사가 놓은 수들을 supervised mapping을 학습 3. policy network를 초기화 - 바둑판의 State를 입력으로 받아 어떤 수(Action)를 둬야하는지를 반환! - policy gradient를 이용하여 지속적으로 학습하며 이전의 자신과 대국을 두며 학습 진행 - 이때 이기면 Reward로 1을 받음 4. value network 역시 학습 5. 최종적으로 Monte Carlo Tree Search와 policy/value network의 결합된 형태가 됨

요약!!