CS231n 10-1. Recurrent Neural Networks(Single RNN) 앞서 본 RNN 모델들은 single layer을 이용하여 hidden state가 하나 뿐 → 더 자주 보게 될 모델들은 multilayer RNN으로 hidden state가 여러개 #RNNLSTM
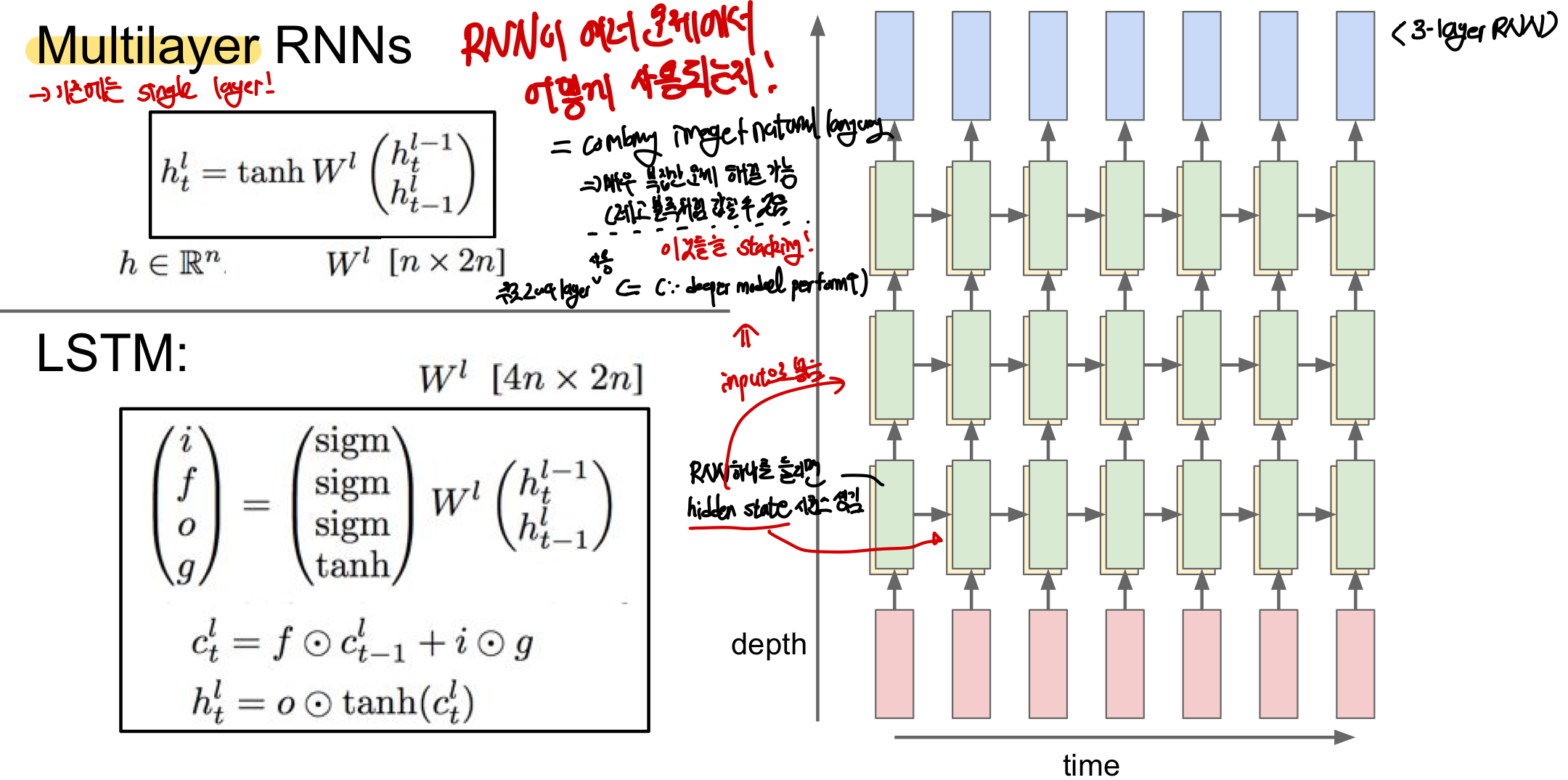
Multilayer RNN
single layer을 사용하지 않고 주로 2~4개의 layer을 겹쳐 RNN을 구성한다
- 입력이 첫번째 layer에 들어가 hidden state를 만들고 이로 인해 만들어진 hidden state를 다시 두번째 layer에 넣어주고 이를 반복하여 구현가능!
- 모델이 깊어질 수록 다양한 문제들에서 성능이 더 좋아짐!
Vanilla RNN Gradient Flow
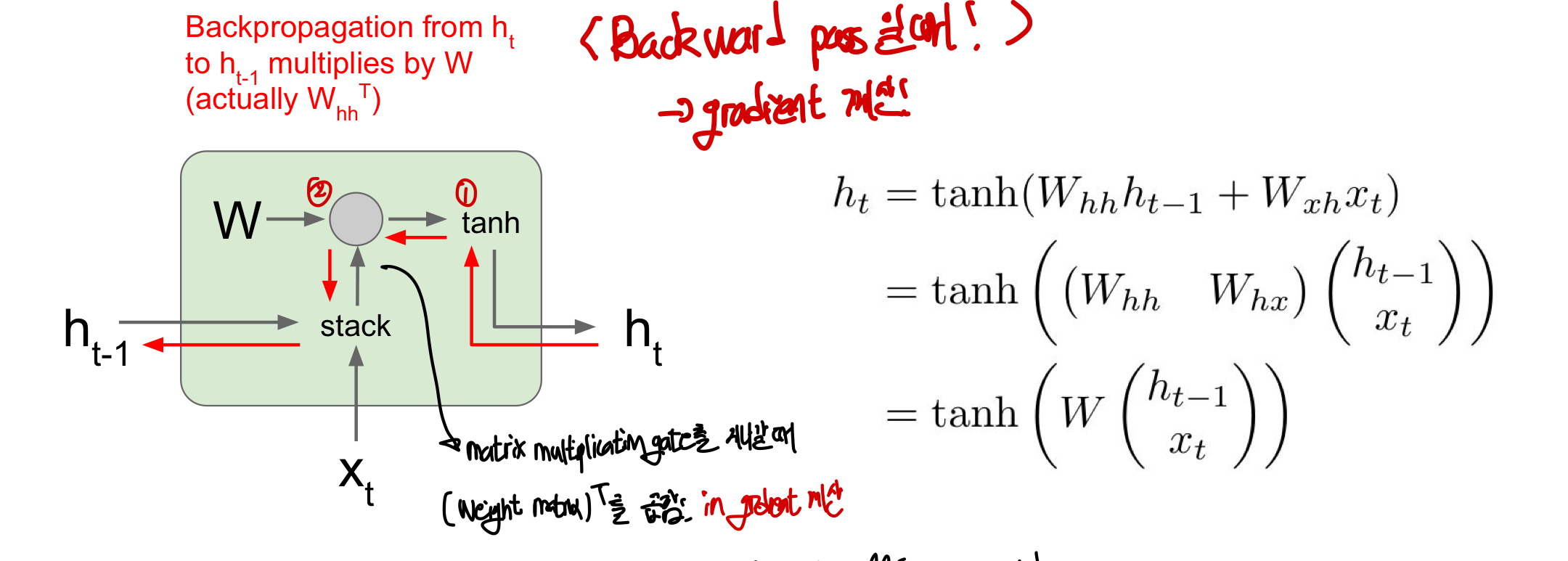
Forward Pass
input x와 이전 hidden state h를 단순히 stack하여 합친 후 weight parameter W와 matrix multiplication 진행
⇒ tanh를 씌운 뒤 다음 state를 만들게 됨!
Backward Pass(gradient 계산)
ht에서 loss의 미분값을 얻어 ht-1의 미분값을 계산하면 됨!
- 이 과정에서 tanh를 지난 후 matrix multiplication gate를 지날 때 transpose(가중치 행렬)을 곱함
- 마지막으로 ht-1의 gradient를 구하게 됨
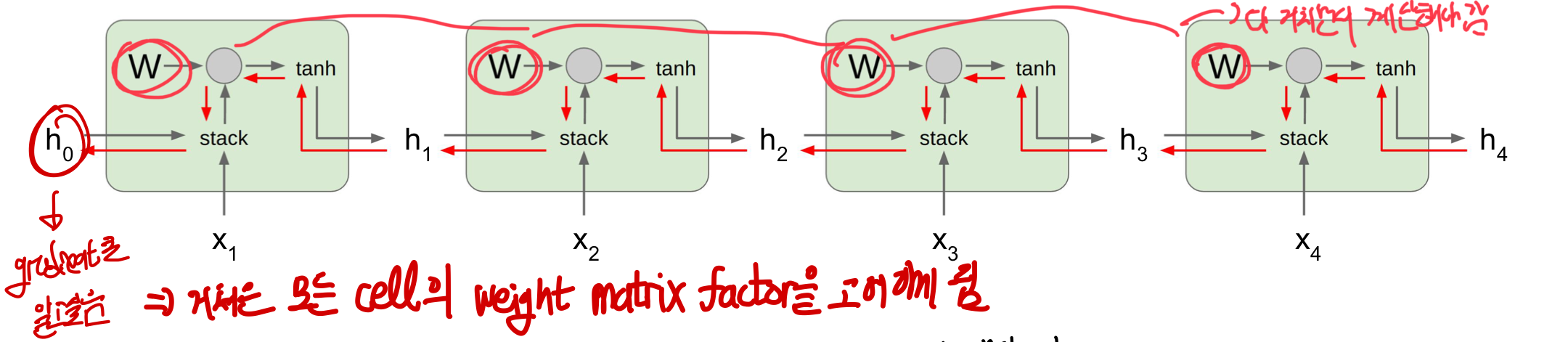
여기에서 문제는 W가 forward와 backward할 때 모두 지나가면서 weigh matrix와 gradient가 곱하게 됨
- RNN 특성상 이러한 sequence가 계속 반복되어 각 cell마다 weigh matrix factor을 고려해야함
- 값이 scalar라고 생각
- W>1: 계속 똑같은 scalar로 곱하게 되면 값이 매우 커져 explode가 됨
- W<1: 계속 같은 값을 곱하게 되면 값이 매우 작아져 vanish!
- 값이 matrix라고 생각해보자
- largest value>1: gradient가 매우 큰 값이 되어 exploding 될거임
- largest value<1: gradient가 매우 작은 값이 되어 vanshing
⇒ 즉, W= 1이 될때만 제대로 학습이 가능!
Gradient Clipping: 임계점을 넘으면 maximum값을 가지도록 값을 줄임!
- 이때 gradient의 값이 L2 norm의 임계값보다 큰 경우 넘지 못하도록 만들 수 있는거임
- 즉, exploding gradient에 대해서는 어느정도 해결함
그럼 vanishing gradient는 어떻게 극복해..?
LSTM (Long Short Term Memory)
동작과정
vanishing과 exploding gradient의 문제를 해결하기 위해 고안되었으며 더 나은 gradient flow를 특성 가짐!
= 한 cell 당 2개의 hidden state(h_t, c_t)가 있는 Multilayer RNN
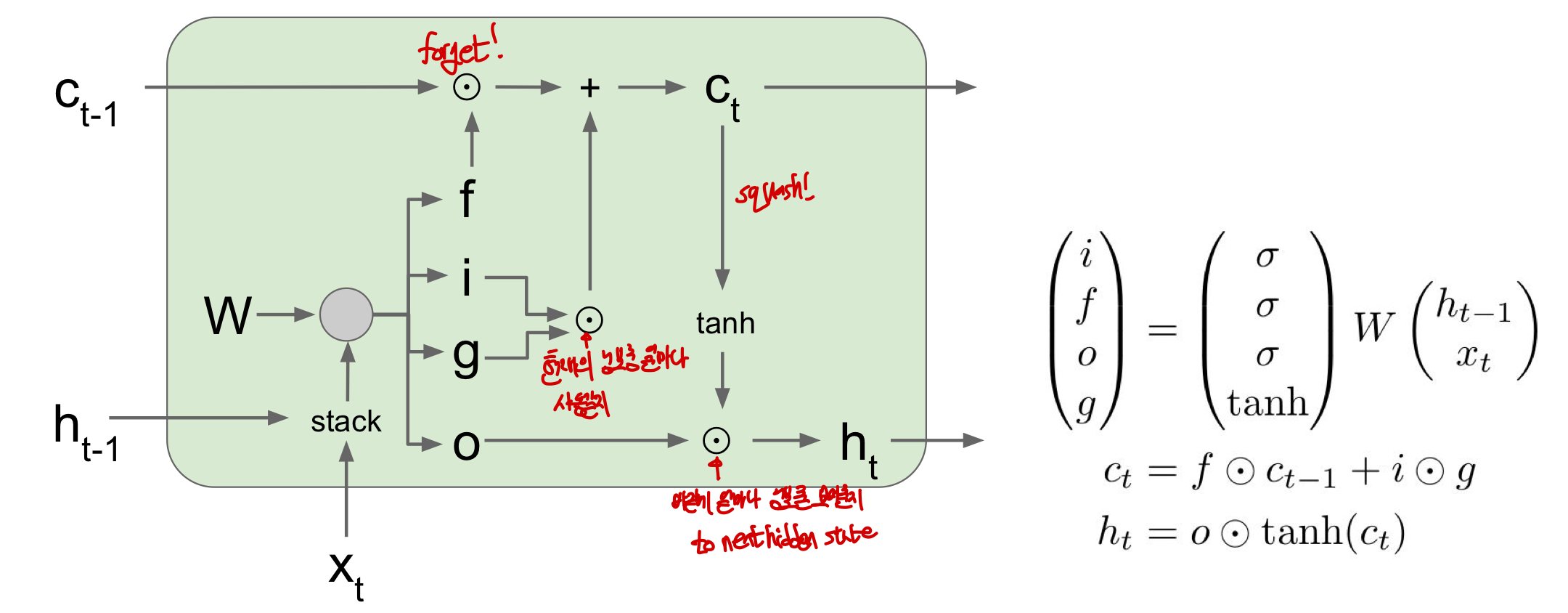h_t : 기존에 봤던 state와 같으며 이전의 state와 새로운 input x로 인해 만들어지는 state!
c_t: LSTM 내부에만 존재하며 밖에 노출되지 않는 변수로 Cell state를 의미
- input: x_t, h_t-1 (h_t가 받는 input과 같을 수 밖에 없음)
- gate: scaler integer counter처럼 값이 줄었다 늘었다 함!
- f (forget gate) : 이전 Cell state를 erase할지를 결정(sigmoid : 0/1값)
- 이전 memory에서 얼마나 정보를 가져올지를 정함!
-element_wise 연산을 이용해 0혹은 기존의 값 둘 중 하나를 가져올 수 있음
- i (Input gate) : 현재의 input에 대해 cell에 정보를 넣을지 안넣을지를 정함(Sigmoid: 0/1값)
- g (gate gate) : cell에 정보를 얼마나 넣을지를 정함 (Tanh : -1~ 1)
- 각각의 값이 -1, +1이 되어 계산이 됨
- 각 step마다 최대 1/ -1씩 세게됨
- o (output gate) : outside world에 cell을 얼마나 보여줄지를 정함
- c_t= f X c_t-1 + i Xg
- 즉, 이전의 cell state에서 정보를 얼마나 가져올지를 정하고 현재의 정보를 얼마나 쓸지를 정한 것이 c_t
-h_t= o X tanh(c_t) : 각각의 cell state의 element를 보여줄지를 정하는 역할!
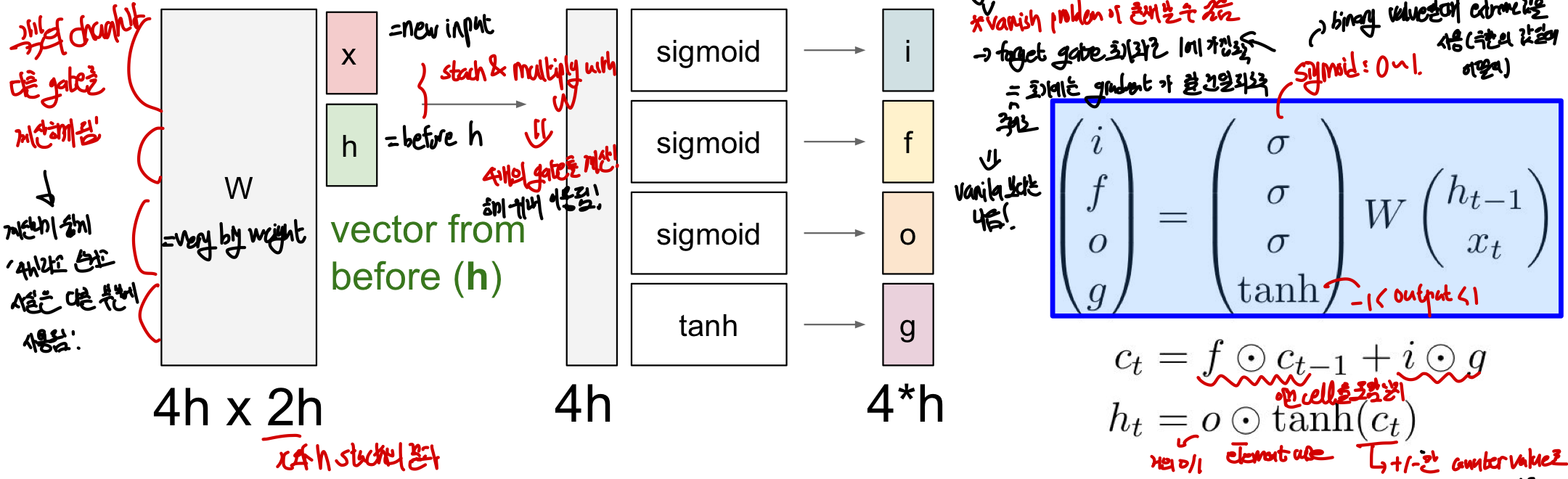이때 W는 very large weight(4hX2h)라고 볼 수 있음
세로의 각 h부분마다 4개의 gate를 계산하기 위해 이용이 되어짐!
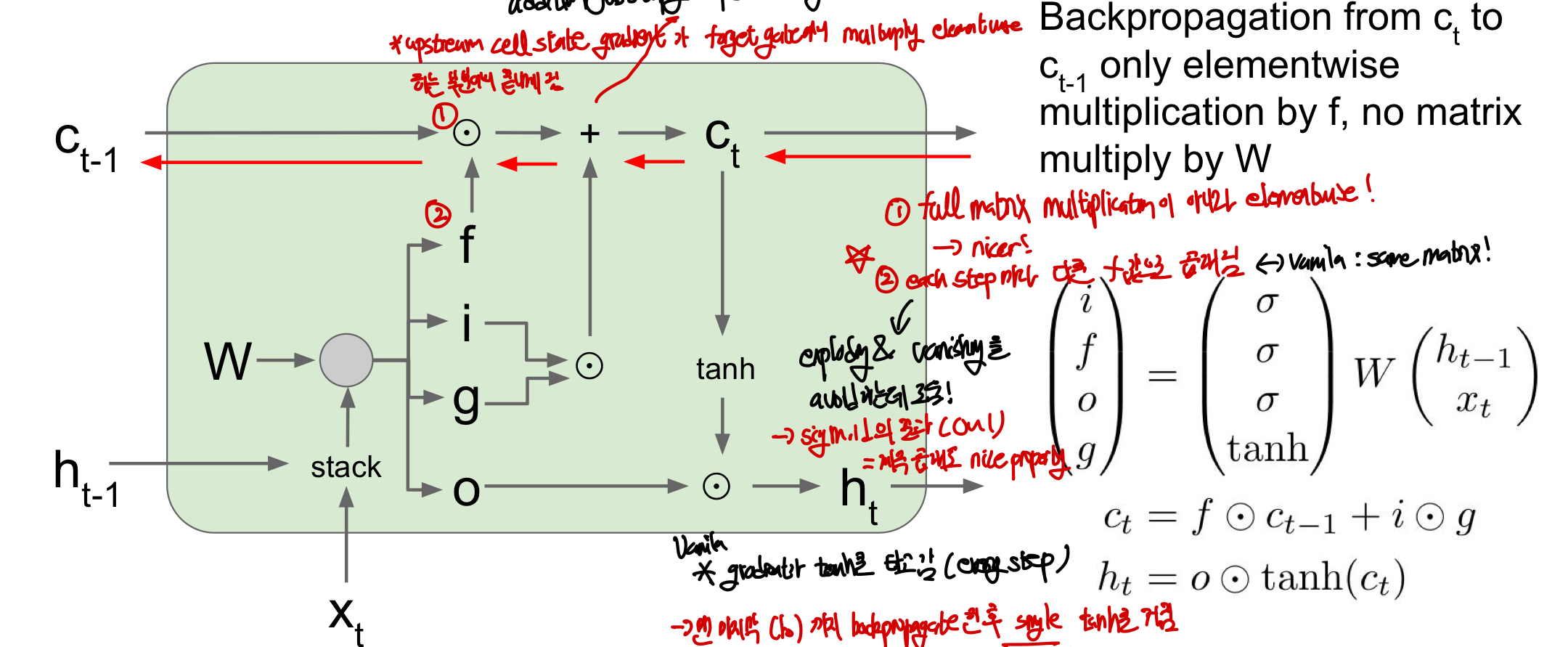
Gradient Flow
Gradient Flow 관점에서 왜 이 방법이 좋을까요???
- full matrix multiplication이 아니라 element wise이기 때문에!! #element_wise: 각 행렬의 원소끼리만 곱하는 것 즉, 각 gate의 과정이 multiplication으로 이루어져있는 것이 아니라 element wise로 이루어져 있기 떄문에 gradient를 구하는 연산이 더 쉬워질 수 있는 것이다 = upstream gradient X forget gate (not W!!)
- each cell step마다 다른 f(forget gate)값으로 곱해지기 때문에 exploding과 vanishing 문제에 효과적! f의 값이 sigmoid의 결과이므로 0~1의 값을 갖고 계속 곱하더라도 nice property를 가짐
- 매 step마다 tanh를 거칠 필요가 없고 처음의 시작한 곳에서 단 한번의 tanh를 거쳐서 backprop을 구함
vanila RNN에서는 매 step마다 tanh를 통한 backprop을 해야함 gradient를 구할 수 있었음
이제는 그렇게 하지 않아도 C_t를 이용하여 gradient를 전달할 수 있으므로 마지막에 한번만 하면 됨
물론 그럼에도 불구하고 gradient vanishing 문제가 생길 수 있음
- 다만, 그 정도가 적음(f값이 매 step마다 다르고 element wise!)
- 적어도 초기에는 gradient가 잘 전달되도록 forget gate 초기화를 1에 가깝도록 만듦
- 학습이 진행되면 f의 bias가 적절하게 조정이 됨
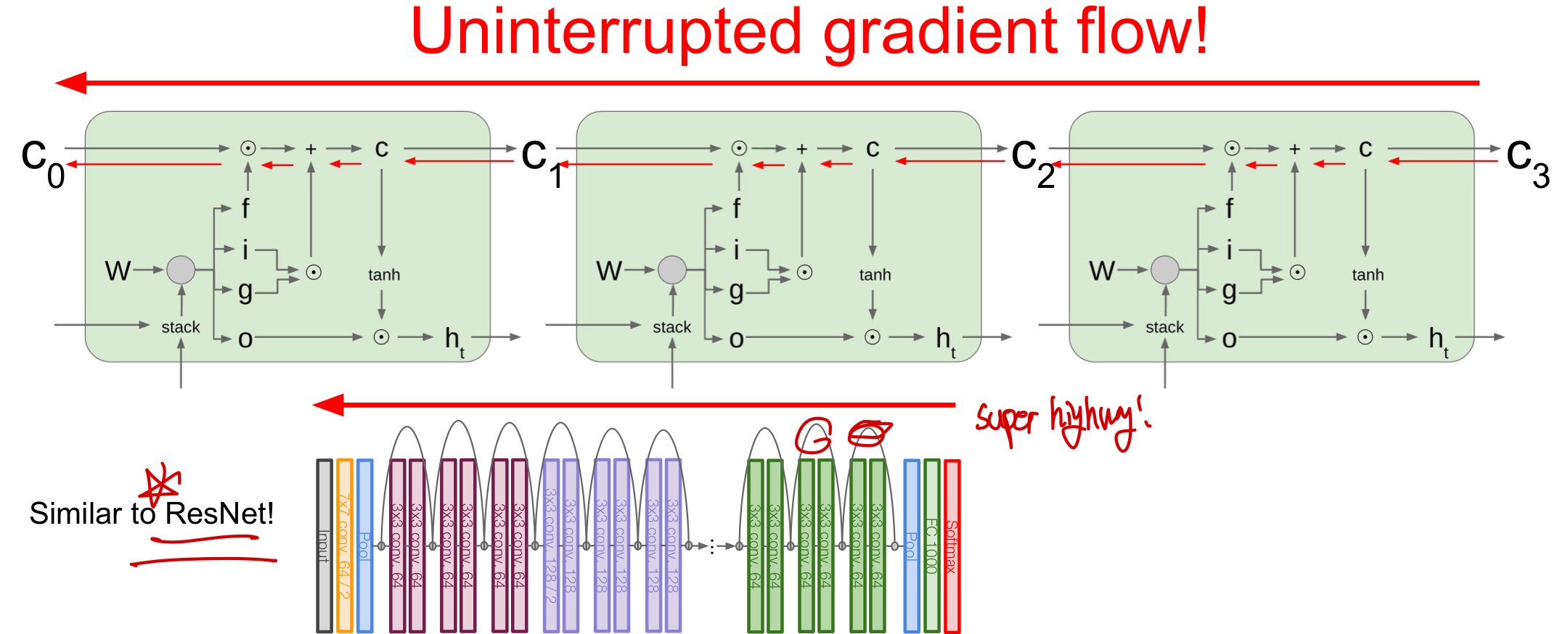
방해받지 않는 일종의 고속도로가 LSTM에서 만들어지며 이는 몇몇 layer 사이마다 값을 직접 전달하는ResNet 과 유사하다고 볼 수 있다.
LSTM에서 W 업데이트는 어떻게 해?
gradient flow를 보게 되면 W를 지나가지 않은데 사실 W가 최적화 되어야 모델이 좋아지는 가장 중요한 부분이잖아!!(vanilla에서는 각 W들이 서로 영향을 미침) A: backpropagation 과정에서 W의 local gradient가 cell과 hidden state로부터 들어오며 cell state가 전달해주어 오히려 더 깔끔하게 local gradient가 전달됨 ⇒ 아마cell state에서 들어온 local gradient를 통해 W를 업데이트 하는 듯..?