CS231n 13. Generative Models

확률곱, gaussian 분포, 확률밀도함수(PMF), covariance, 베이즈룰

Unsupervised Learning

---

지금까지 우리가 배웠던 모델은 대부분 supervised learning을 이용했으며 data의 label이 존재하며 실제 값과의 loss를 최대한 줄여 최적화시키는 것을 목표로 했다. 이번에 새롭게 다루는 것은 비지도학습, unsupervised learning으로 모델 스스로 특정 실제값이 존재하지 않고 스스로 학습하는 것이 특징이다.

Supervised learning

• Data: $X$= input될 data, $Y$=label data(ground truth)
• Goal: $X$를 $Y$에 mapping 시키는 함수를 학습시키는 것이 목표
• example: Classification,Regression, object detection, semantic segmenatation, image captioning CS231n 11. Detection & Segmentation

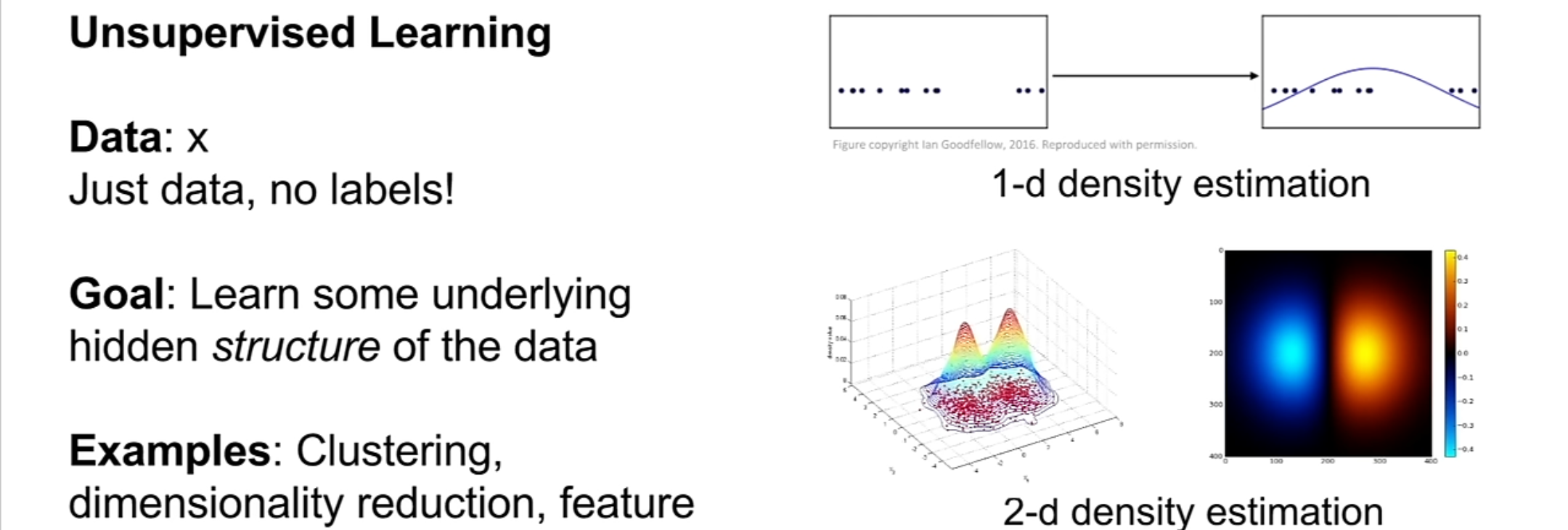
Unsupervised Learning

• Data: label data가 따로 존재하지 않으며 데이터 그 자체를 학습하고 training data에 labeling을 따로 할 필요가 없기 때문에 비용면으로 싸다고 할 수 있다
• Goal: data의 중요하고 숨겨진 구조를 학습하는 것!
• Example:
  • Clustering 20. Clustering With K-Mean
  • dimensionality reduction: 주로 PCA를 쓰며 고차원의 데이터 분포를 저차원으로 만듦 CS231n 6-3. PCA & Whitening 21. Principal Component Analysis(PCA)
  • feature learning: feature을 학습시키는 것으로 input과 autoencoder을 통한 output의 차이를 최적화함으로써 학습을 진행하는 방식이다autoencoder
  • density estimation: data의 density를 구하는 것으로 data의 density를 높게 만드는 것이 좋다. 이때 데이터의 밀도를 추정하는 통계학적 기법으로, 새로운 데이터가 어떤 확률 분포에 속하는지 예측하며 unsupervised learning에서 가장 중요한 문제 중 하나이다.

Generative models

이번 강의에서의 우리의 목표는 입력 data(image)와 똑같은 분포를 갖는 output data(image) 를 unsupervised learning을 통해 만드는 것이다! 즉 $p_{model}$함수를 $p_{data}$함수와 최대한 비슷하게 학습시키는 과정이다.

학습 data가 들어왔을 때 이 data들의 분포를 학습하여 최대한 비슷한 분포 찾아내 여기에서 새로운 data를 sample하는 방식으로 이루어진다. 또한 이것은 데이터의 분포를 알아내는 density estimation을 사용한다고 볼 수 있다. 이러한 generative model은 새로운 사진을 만들어내는데 사용될 뿐 아니라 시계열 데이터들이 강화학습에서 특정 상황을 만들어내고 계획하는데 활용된다. 이런 식으로 generative 학습을 할 경우 데이터 안에 들어있는 숨겨진 특징들(latent feature)을 추론할 수 있다는 점에서 이점을 가진다.

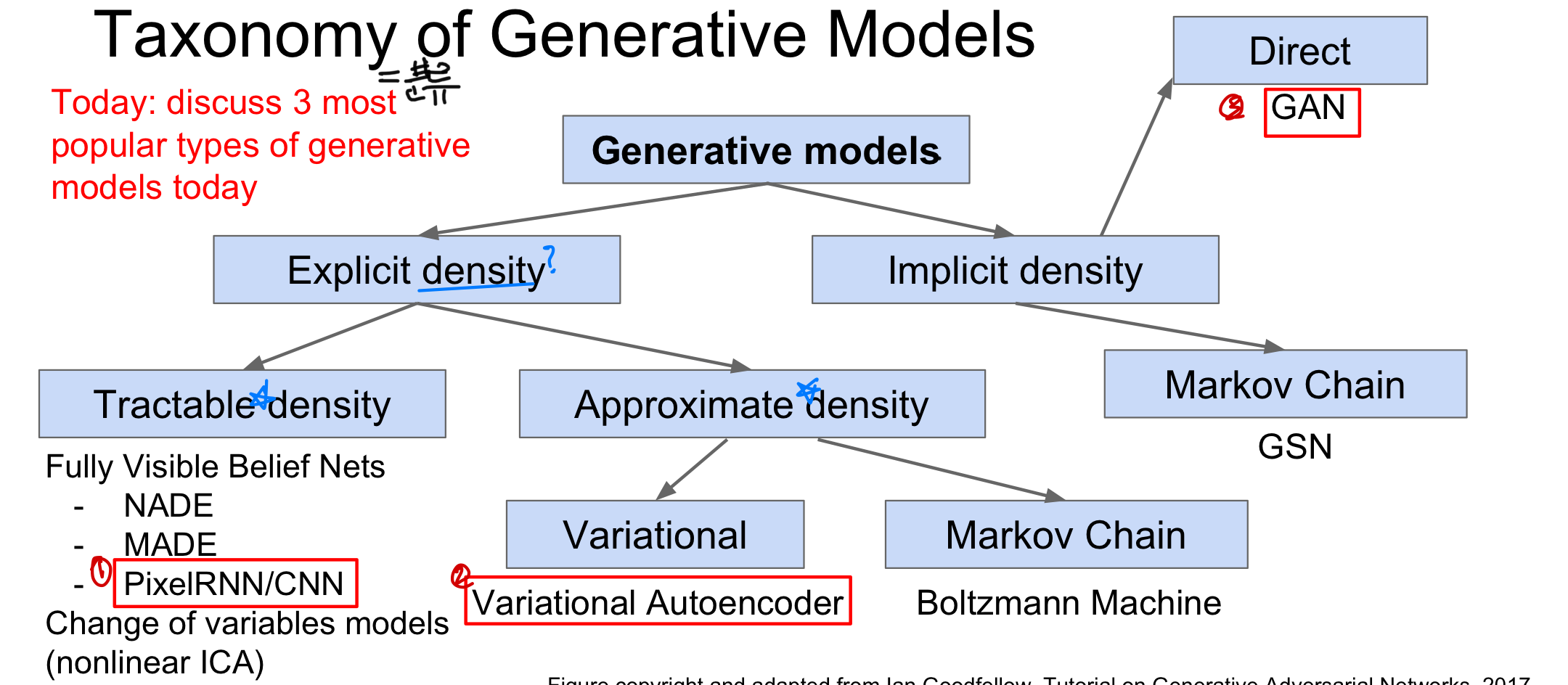
Generative Model의 분류

• Explicit density: 모델이 생성하는 확률 분포가 명시적으로 정의된 확률밀도함수(PDF)로 나타낼 수 있을 때 사용한다.
  • density: 변수가 특정 값 또는 범위에 얼마나 집중되어있는지로, PDF에서는 변수가 특정 값에 속할 확률을 나타내며 이러한 density를 정확하게 tractable할 수 있느냐에 따라서 다시 모델이 나뉘게 된다.
• Implicit density: 명시적으로 정의된 확률밀도함수는 없으나 새로운 분포에서 sample할 수 있는 모델을 학습시키는 것을 의미한다. 즉, $p_{model}$에서 sample을 한다고 볼 수 있다.

Pixel RNN

---

위에서 언급한 explicitly density model로 변수가 특정 값에 속할 확률을 정확하게 구하고, 이러한 정확한 확률로 최적화 진행하는 fully visible belief network이다.

동작 방법

1. 입력 image x의 확률을 chain rule을 통해 1차원 distributin의 곱으로 decompose!
2. 이후 training data의 확률을 최대화하는 것을 목적으로 함! pixel들의 value들이 복잡한 distribution을 갖고 있기 때문에 Neural Network를 이용해 표현! - 복잡한 분포를 갖는 모든 pixel에 대해 계산하는 것이 어려움 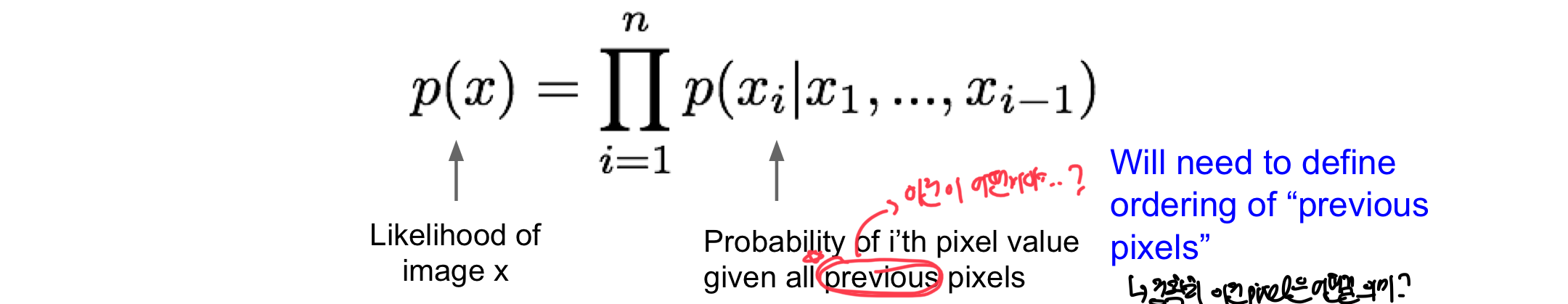여기서 말하는 previous pixel이 어떤 것인지에 따라 2가지 방법으로 나뉨(RNN방식 /CNN방식)

CS231n 10-2. Multilayer RNN 왼쪽 위 픽셀에서부터 시작하여 이미지 픽셀 값을 만드는데, RNN(LSTM)을 이용하며 이전의 pixel 값에 의존하여 진행이 된다. 이때 의존하는 pixel은 화살표로 연결되어 있는 것을 의미하게 된다. 즉, 이전 pixel 값에 의존하기 떄문에 정확한 확률로 값을 예측할 수 있는 explicit density를 갖는다 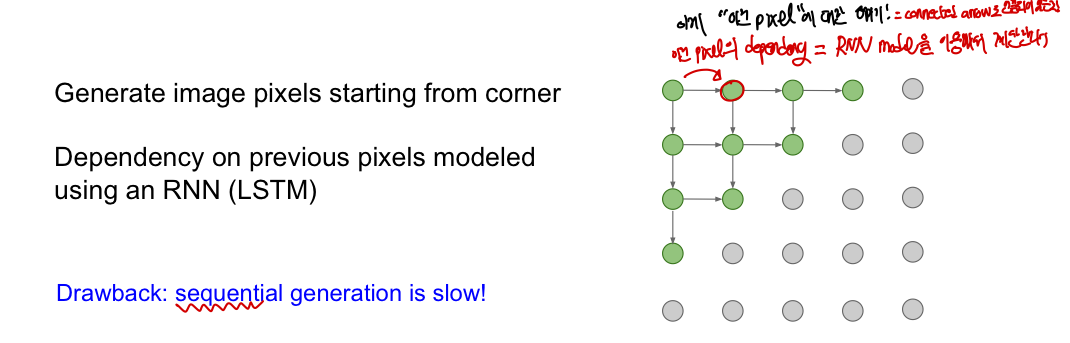단점: pixel의 계산이 이전 pixel에 영향을 받으며 CNN과 같이 한번에 계산되는 것이 아닌 순차적인 생성이 되기 때문에 느리다.

PixelCNN

---

CS231n 5. Convolutional Neural Network (CNN) 여전히 왼쪽 위 코너부터 pixel이 만들어지게 되는데 이때 Pixel RNN과의 차이점은 새로운 pixel을 만드는 과정에서 RNN을 사용하는 것이 아닌 CNN을 사용한다는 것이다. 이때 사용되는 이전의 픽셀들은 화살표로 연결된 부분이 아닌, 일종의 context region(filter)에 들어가는 픽셀들로, 이 픽셀들을 이용해 다음 픽셀이 어떤 값일지 예상하게 된다.

이때 학습은 각 픽셀마다 softmax loss를 이용해 예측한 값과 실제(학습 이미지) 값을 비교함으로써 진행된다. 즉, 각 pixel 위치마다 어떤 pixel 값을 가지게 될지에 관한 분포를 만들게 되고 이를 실제 값과 비교한다는 의미이이며 실제 값이 뽑힐 가능성이 높게 분포를 만드려고 한다 ➡️ 이 비교하는 과정이 지도학습처럼 생각할 수도 있지만 이때 비교하는 값은 입력 이미지이기 때문에 추가적인 labeling이 필요하지 않아 비지도 학습이라고 봐야한다 결국 training data pixel의 likelihood를 최대화하도록 만들어 실제 입력 이미지와 유사하게 만들게 된다

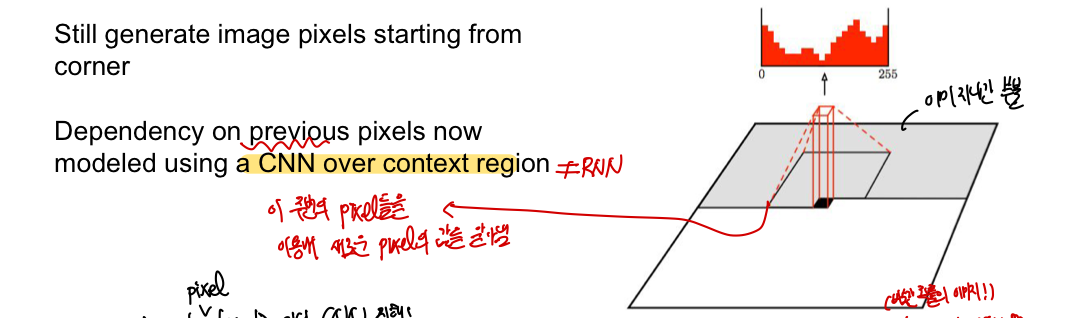
• 장점: PixelRNN보다 training이 빠르다 ➡️ training image으로부터 context region의 값을 알고 있기 때문에 병렬적으로 학습이 가능하다. 이때 tractable density를 매우 잘표현할 수 있고 정확한 likelihood를 구할 수 있음
• 단점: 여전히 이전에 계산된 pixel들이 필요한 seqeuntial한 방법이기 때문에 느리다 - 맨 첫번째 pixel에 따라 chain rule을 진행하기 떄문에 이 pixel이 바뀌면 전체적인 값이 바뀔 수 있음 한꺼번에 pixel들을 처리할 수 있는 방법을 이후에 알아볼거임! 또한 성능으로도 더 향상된 방법을 알아볼거다!

Variation Autoencoders (VAE)

직접적으로 density 함수에 대해 최적화가 불가능하게 만드는 대신에 lower bound의 likelihood를 구하여 간접적으로 최적화하는 방식이다. 먼저 Autoencoder에 대해서 알아본 뒤에 VAE에 대해서 알아볼 것이다!

Autoencoder

---

data를 낮은 차원에서 feature representation을 구하는데 사용된 후(크게 encoder와 decoder로 이루어짐) 새로운 형태의 데이터를 만들어내는 구조이다. 즉, encoder을 이용해 feature을 학습하고 decoder을 이용해 다시 데이터를 복수하는 형식으로 이루어진다.

Encoder

• 입력 data x에서 숨겨진 feature z를 구하기 위해 function mapping이 사용된다. 즉, 함수를 통해 학습을 하여 feature을 만들어낸다
• 처음에는 단순한 linear function을 사용하다가 현재는 주로 ReLU를 이용한 CNN을 사용
• feature $z$를 구할 때 차원이 축소되는데, 이는 데이터의 중요한 variation 요소를 알아내기 위해서이며 중요한 부분의 정보만 추출하고 안중요한 정보는 버리는 것이 효과적이기 때문이다

Decoder

• feature $z$를 입력으로 받아 본래의 입력 데이터와 유사하게 재구성을 진행한다
• 요즘에는 CNN의 upconv를 이용해서 주로 구성함

Loss function

• input data($x$)와 reconstructed data($\hat{x}$)를 유사하게 만들기 위해 따로 classification 문제처럼 ground truth label을 사용하지 않고 둘 사이의 차이를 통해 loss를 구하는 L2 loss function을 사용한다.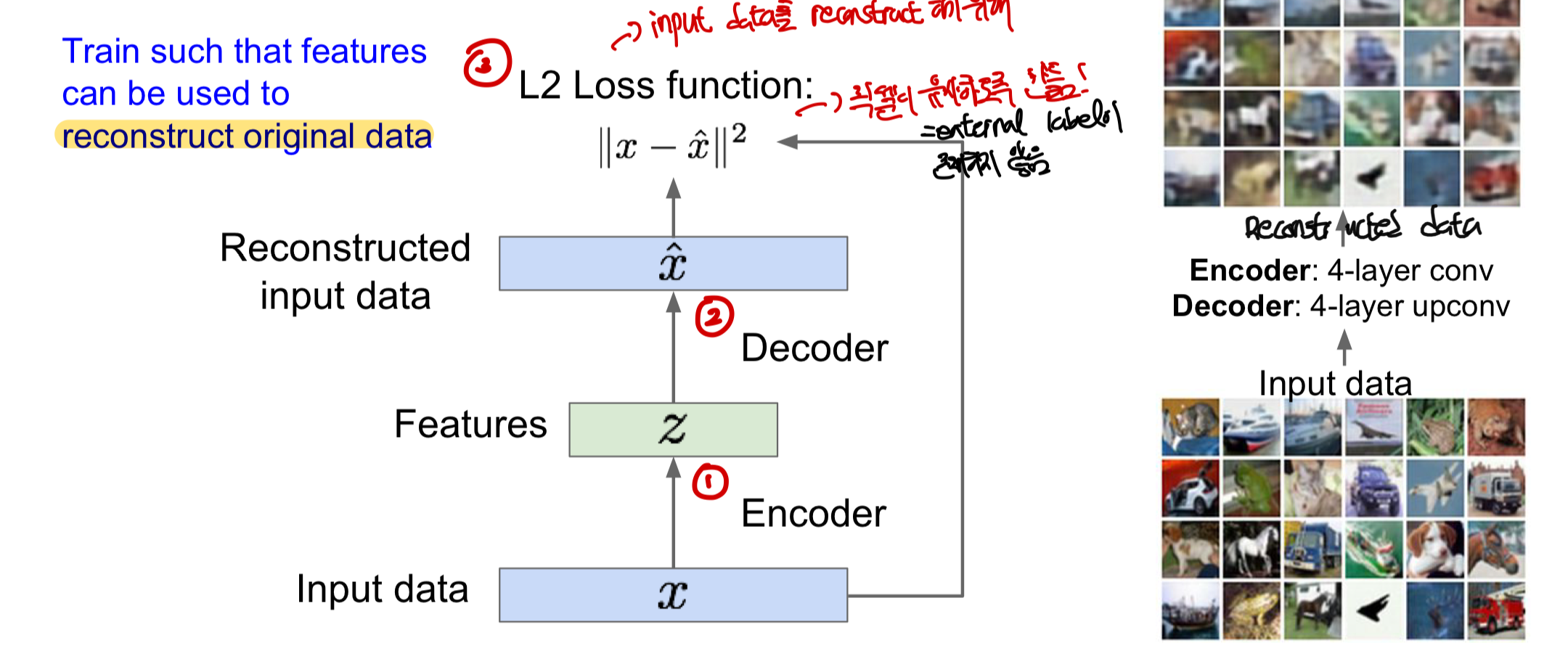

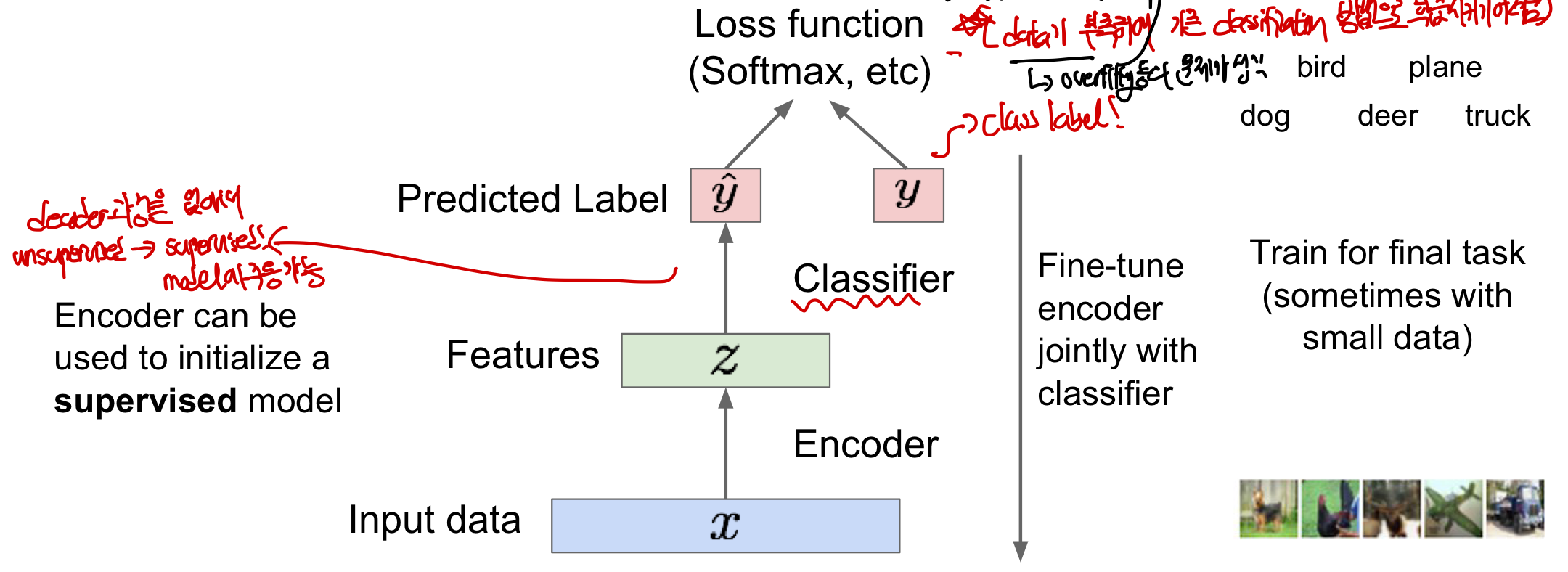
Throw away decoder 위의 3가지 encoder,decoder,loss function을 통해 모델을 학습시킨 후 decoder와 loss function 부분을 없애는데 이는 단지 모델을 학습시키기 위해 필요한 부분이기 때문이다. 이를 통해 입력 data x가 encoder을 지나면서 중요한 feature $z$만 추출하도록 만들게 시킨 후, feature $z$를 보고 예측한 class와 실제 class 사이의 loss function(softmax)등을 이용하여 fine-tuning하여 더 효과적으로 classifcation이 가능하게 된다

즉, labeling 되지 않은 training data를 이용하여 비지도학습으로 일반적으로 좋은 feture을 만들 수 있는 모델을 만들 수 있고 이를 이용해 적은 수의 data들을 가지고도 매우 효과적으로 학습이 가능해진다. 이러한 이유로 주로 data가 부족하여 기존 classification 방법으로 학습시키기 어려울 때 많이 사용하며 data가 부족하면 과적합 문제가 발생하게 되는데 과적합의 본질적인 해결방인 data의 수를 늘리는 것이므로 효과적인 해결방인이 된다.

Variational Autoencoders

---

위에서의 autoencoder의 경우는 비지도 학습을 통해 feature $z$를 학습시키고 이를 적은 양의 데이터만으로 지도학습이 가능하게 만들었다. 여기서 다루는 variational autoencoder의 경우는 여기에서 더 나아가 새로운 이미지 데이터를 만들기 위한 모델이라고 보면 된다.

training data $x$는 숨겨진 feature(latent factor) $z$에 의해서 생성되었다고 가정을 하는데, 이때 $z$는 실제 분포에서 sample 되었다고 보고, $x$는 이 실제 조건에서 sample되었다고 본다. 예를 들어 $z$가 사람이 얼마나 많이 웃고있는지에 대한 실제 분포(ex: gaussian)에서 하나의 값을 sample한거라면, 이러한 사람이 특정값만큼 웃는 $z$가 주어졌을 때 어떤 이미지를 가질지 sample한 것이 $x$이다.

• latent factor $z$: feature을 저장하고 있으며 사람이 얼마나 웃고 있는지, 눈썹의 위치등의 정보를 담은 vector로 이 factor을 이용해 image $x$를 만들어낸다
• prior: 확률분포관점에서 어떠한 event(사건)이 일어날지에 대한 기대값으로 어떤 사건이 발생하기 전에 해당 사건에 대해 가지고 있는 사전지식이라고 볼 수 있다. 사후확률(posterior)를 갱신하기 이전 가수/모수에 대한 믿음으로 latent variable z의 초기분포를 의미(여기서는 주로 Gaussian을 따름)한다.

우리가 원하는 것은 이 generative model의 실제 parameter ${\theta }^{\ast }$를 추정 하여 입력 data와 매우 유사한 재구성 data를 만들어내는 것이다. 그렇다면 이 모델을 어떻게 표현할 수 있을까?

먼저 prior $p(z)$는 모르는 분포이기 때문에 대부분의 자연법칙에 적용되는 gaussian과 같은 분포를 고르는 것이 일반적이다. 여기서 문제는 $p(x|z)$를 구하는 것인데 이는 이미지를 생성하는 decoder 부분이기 때문에 neural network를 이용해 복잡하게 표현이 된다.

그렇다면 이 모델을 어떻게 학습 시킬까? data의 likelihood를 최대화하는 parameter들을 구하면 되는데 여기서 문제는 $p(x)$를 구하는 식이 무한대로 복잡하여 다루기가 어렵다. 즉, 단순히 적분하여 likelihood를 구하는 것이 불가능하다.

• likelihood(우도): 어떤 관측값이 특정한 모델에서 얼마나 자주 발생할 것으로 예상되는지를 나타내며 $Likelihood(\theta ;D)=P(D|\theta )$ 로 모델 매개변수 $\theta$에서 데이터셋 D가 나올 확률을 의미한다.즉, parameter들을 학습시켜 input data가 다시 output으로 나올 확률을 최대화시키는 과정이라고 보면 된다likelihood

Likelihood of parameter와 probability of data는 완전히 같음

• probability of data: parameter가 고정되어 있고 data(variable)이 변화할 때 사용되는 개념
• Likelihood of parameter: training set에서 data(variable)가 고정되어 있고 parameter을 변화시킬 때 사용 즉,likelihood of parameter와 probability of data는 관점에 따라 용어만 다를 뿐 똑같은 뜻이다!

Intractability

1. 모든 z에 대해 x가 sample될 확률을 구할 수 없음 $p_{\theta }(z)$: Gaussian 분포를 따르고, $p_{\theta }(x|z)$는 neural network의 decoder 부분을 이용하기 때문에 계산이 가능하다. 하지만 결국 우리가 구하고자 하는 것은 $x$가 뽑힐 확률이 가장 높게 만들어 입력 데이터와 가장 유사하게 만들어야하는데,$p_{\theta }(x)$의 값을 단순히 적분을 통해 얻을 수 없다, 즉, 두 확률 분포의 곱이 복잡한 형태이기 때문에 모든 $z$에 대해 적분이 불가능한 형태이다.

2. 사후분포(posterior density) 역시 intractable $p_{\theta }(x)$의 값을 알 수 없어 계산이 불가능하다. 이때 posterior density(사후분포)은 적절한 잠재변수 표현(latent variable)을 사용하기 위해 주로 이 분포를 사용하지만 이것 역시 intractable하기 때문에 의미있는 재구성된 data를 만드는 과정을 계산하지 못한다.

 즉, 이와 같은 2가지 이유로 인해 기존의 방법대로 모델을 학습하여 parameter $\theta$ 최적화를 진행할 수가 없다. 해결책 $p_{\theta }(z|x)$를 근사한 추가적인 encoder network $q(z|x)$를 정의함으로써 이를 최대한 $p(z|x)$의 근사하여 data likelihood(우도)의 lower bound를 제공하여 parameter $\theta$에 대한 최적화가 가능하도록 만든다

Optimize 과정 (parameter theta)

1. 확률적인 관점에서의 encoder, decoder network 생성 및 해석 input data(x)를 잠재공간의 확률분포로 mapping(z space) 후 잠재공간의 점을 sample하고 특정 확률 분포에 근사시켜 데이터 학습 1-1. encoder network(x→z): input data x에서 평균과 공분산을 추출 후 z space 상에서 분포를 생성 - 주로 gaussian 분포를 따름 - 이 분포에서 z를 sample하게 됨! - inference network로 불림: latent z이 어떨지에 대한 추론을 하고 있기 때문! 1-2. decoder network(z→x): feature variable z를 sample(encoder에서 구한 분포에서!) - z를 가지고 x space 상에서 확률분포를 생성하고 이 분포에서 sampling! - generation network로 불림: 새로운 이미지를 만들기 때문에! 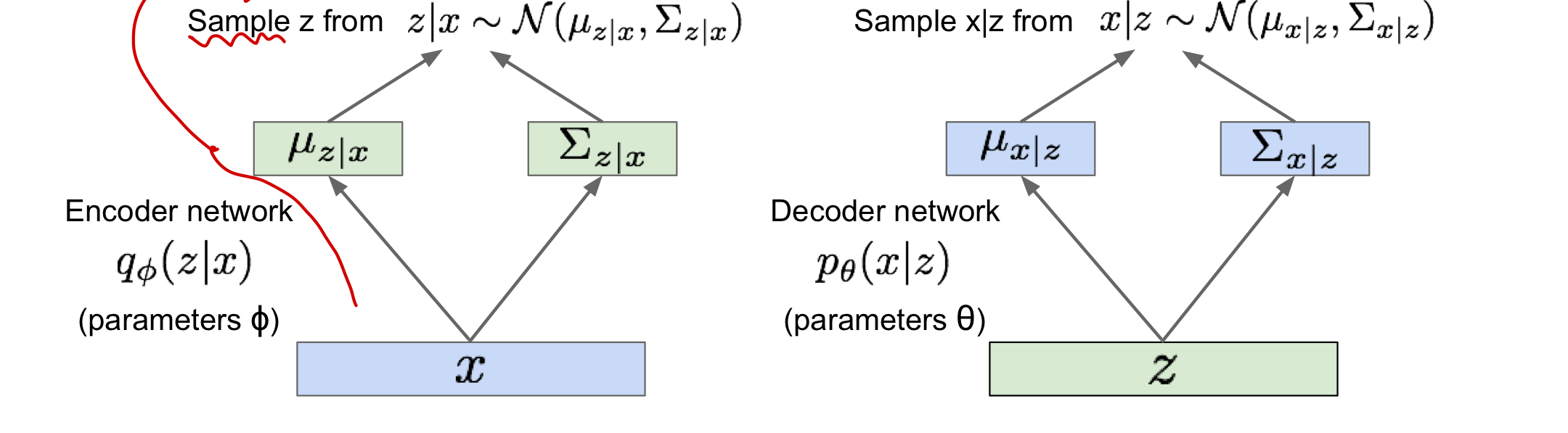2. data likelihood(우도) 계산!! encoder와 decoder network를 만들었으니 data likelihood를 계산하여 식을 만들어 optimize할 수 있도록 식을 전개해보자! (우리가 원하는 값은 p_th(x)의 값!) 2-1. encoder network에서 sampling한 z가 있으며 p(x)의 log값을 취한후 expectiation을 취함 - log값을 취한 이유: 계산의 용이성(곱셈→덧셈) & KL divergence 계산에 필요 - z에 관한여 expectation을 구하는데 이는 후의 계산에서의 유용성 때문에 함 - 근데 왜 expectation을 써서 1번에서의 항등식이 성립되는지는 모르겠음 2-2.Bayes_Rule 을 이용해 식을 변환 2-3. 상수를 곱해줌(1=q_pi(z|x)/q_pi(z_x)) 2-4. 로그의 기본 성질을 이용해 3개의 항으로 나누어 각 항에 따라 해석이 가능하게 만들어줌 2-5. 각 항마다 해석! 1. Computatble! - p_th가 decoder network이고 feature variable z에서 x를 sample하는 것이기 때문에 compute 가능 - sampling과정에서 미분이 가능하게 만들어주는 reparam 기법을 사용한다고 함 2. Computatble! - q_pi는 encoder p_th는 decoder network인데 q_pi에서 input data x에 대해서 z를 sample, p_th에서 feature z를 단순히 sample하고 있어(prior과정) computable - 이때 encoder에서의 분포와 prior에서의 분포가 모두 gaussian이기 때문에 KL을 통해 매우 간단하게 계산가능 - KL divergence: 요약하자면 두 확률 분포사이의 차이를 측정(얼마나 같고 다른지!) - latent variable의 분포를 prior 분포와 가깝도록 유지하고 z space의 표현을 부드럽게! 3. Intractable (Not Computable) - p_th는 decoder network이고 이때 x에 대해서 z를 sample할 수 없음(위의 Intractability의 사후 분포에 나와있음 → 우리가 그래서 이에 근사치인 q_pi를 사용한거임) - 다만 KL divergence는 두 분포가 얼마나 차이가 나는지를 설명한 지표이기 떄문에 0보다 크거나 작다는 것을 알고 있음 2-6. 위에서의 1,2번 항은 계산이 가능하기 때문에 이 부분은 gradient를 구할 수 있고 최적화시킬 수 있음 - p(x|z)와 KL은 모두 미분이 가능 - 또한 3번째항은 0보다 크기 때문에 tractable lower bound라고 말할 수 있음! 2-7. 여기서 구한 lower bound보다는 p(x)가 크다는 뜻이기 때문에 p(x)를 최대화하기 위해서는 lower bound를 최대화 해야한다 - lower bound를 최대화하기 위해 pi와 th에 대한 최적화를 계속 진행하여 training! 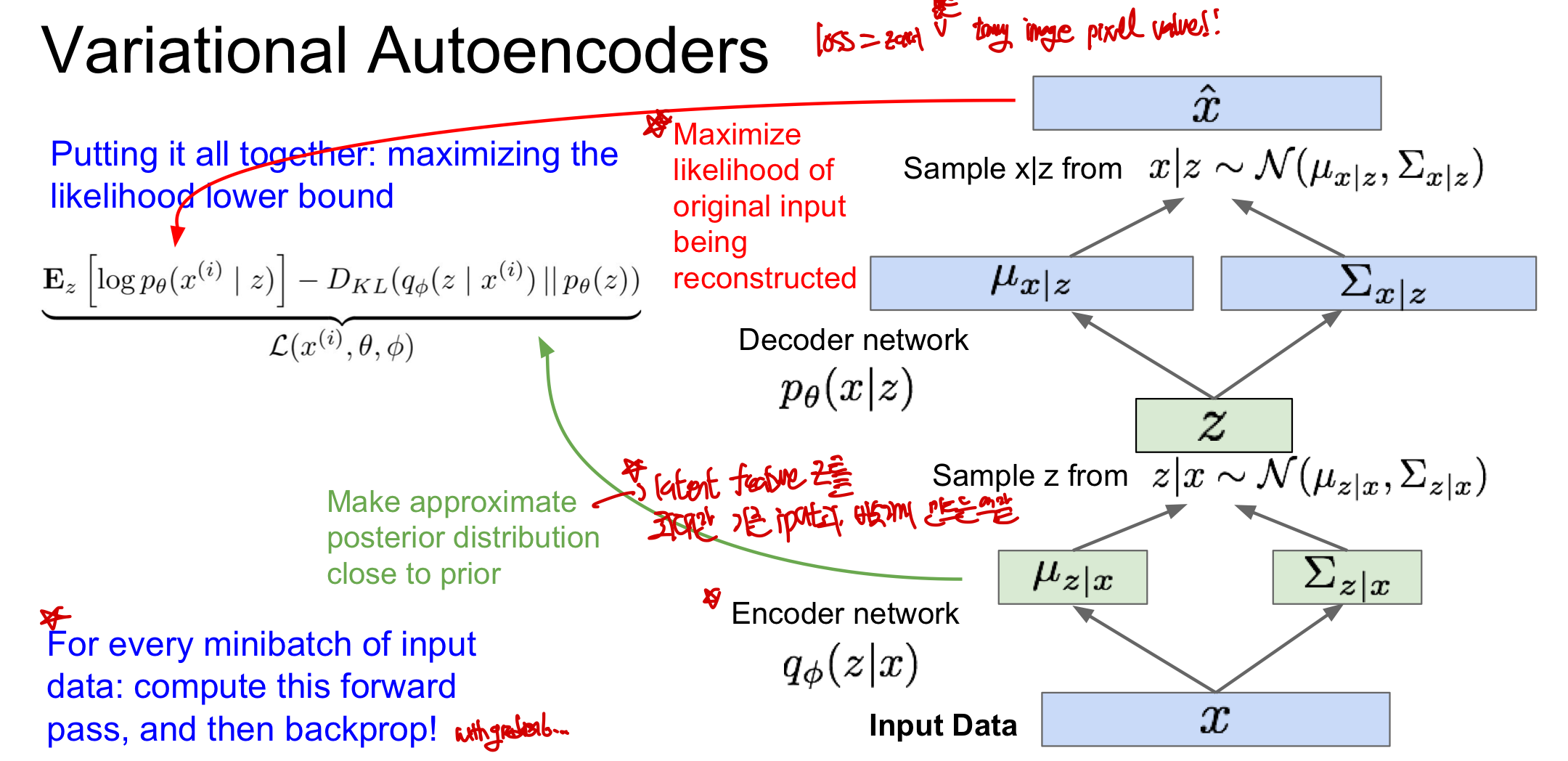3. lower bound를 최대화하기! 3-1. input data를 reconstruct한 data가 기존 data와 유사하도록 만들어야함!(p(x|z)) 3-2. posterior 분포와 prior 분포를 유사하게 만들어 KL divergence값을 작게 만들어야함! 이 3-1을 증가시키고 3-2를 감소기키는 방향으로 backpropagagtion을 진행하여 parameter pi와th를 업데이트해 train data likelihood를 최대화 시킨다

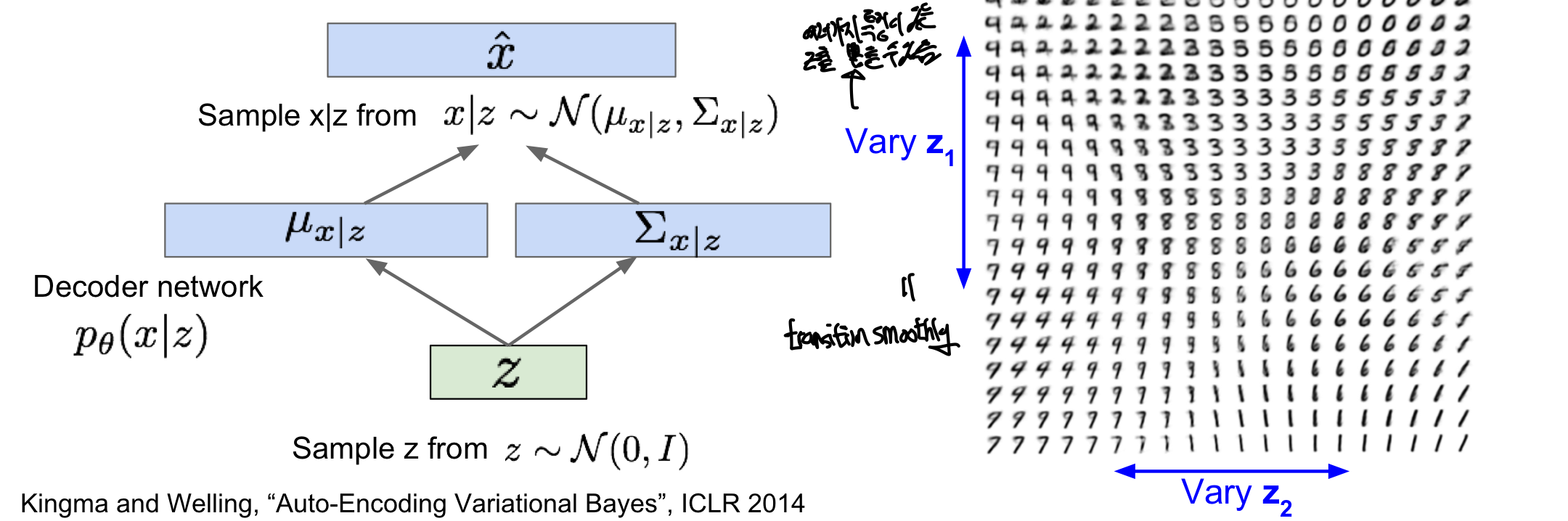
Generating Data!

training때는 encoder가 필요하지만 학습완료되면 decoder만을 이용하여 image를 만들 수 있음 - latent variable z간의 독립을 가정하게 된다면 2차원 상에서 특정 특성을 시각적으로 확인 가능 - encode 과정에서 서로 다른 interpretable semantics을 표현가능해진다(z가 좋은 feature을 갖는다!) - 얼마나 좋은 latent feature인지는 q(z|x)를 계산을 통해 알 수 있다 - 이러한 z를 통해 classification이나 새로운 사진의 생성과 같은 데에 사용이 가능함 장점: - Generative model에 대한 명시된 방법으로 계산이 가능(principled approach) - q(z|x)에 대한 추론 (inference)가능하여 다른 일에서 feature representation에 유용해짐 - z가 얼마나 좋은지, 어떤 특성을 가지고 있는지에 대해서 명시적으로 알 수 있게 됨 단점: - Pixel CNN/RNN과 같이 evaluation이 좋지 않음(정확한 값으로 나오지 못함 by lower bound) - lower bound 때문에 정확한 값으로 최적화가 진행되지 못해 엄밀하지 못함 - GAN에 비해 성능이 좋지 않음(blurrier & low quality)

Generative Adversarial Network (GAN)

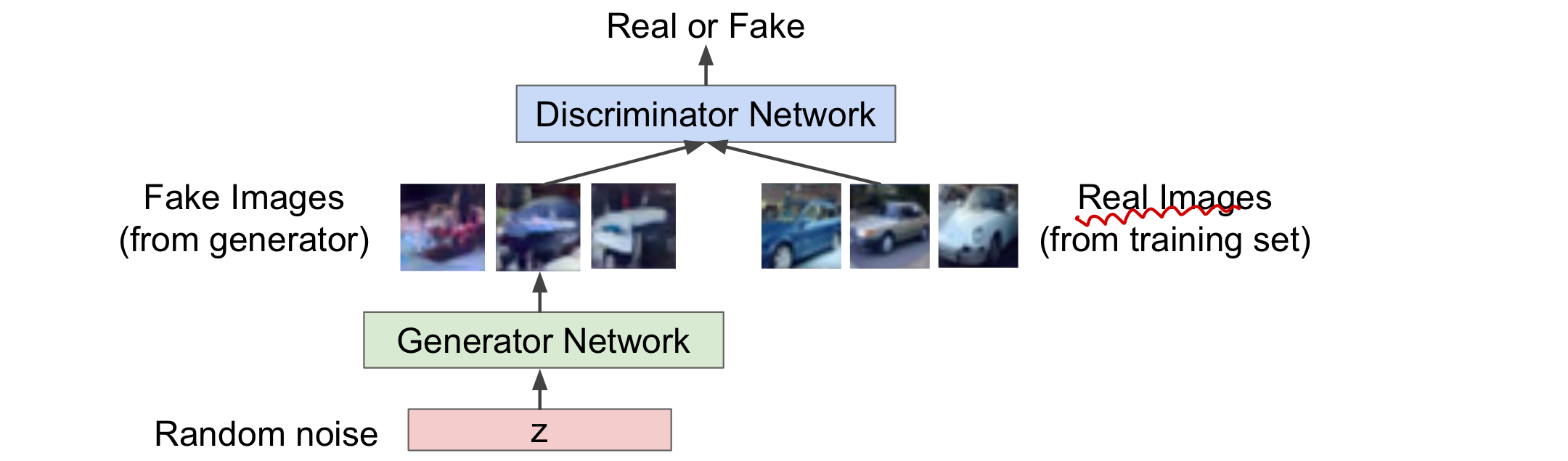
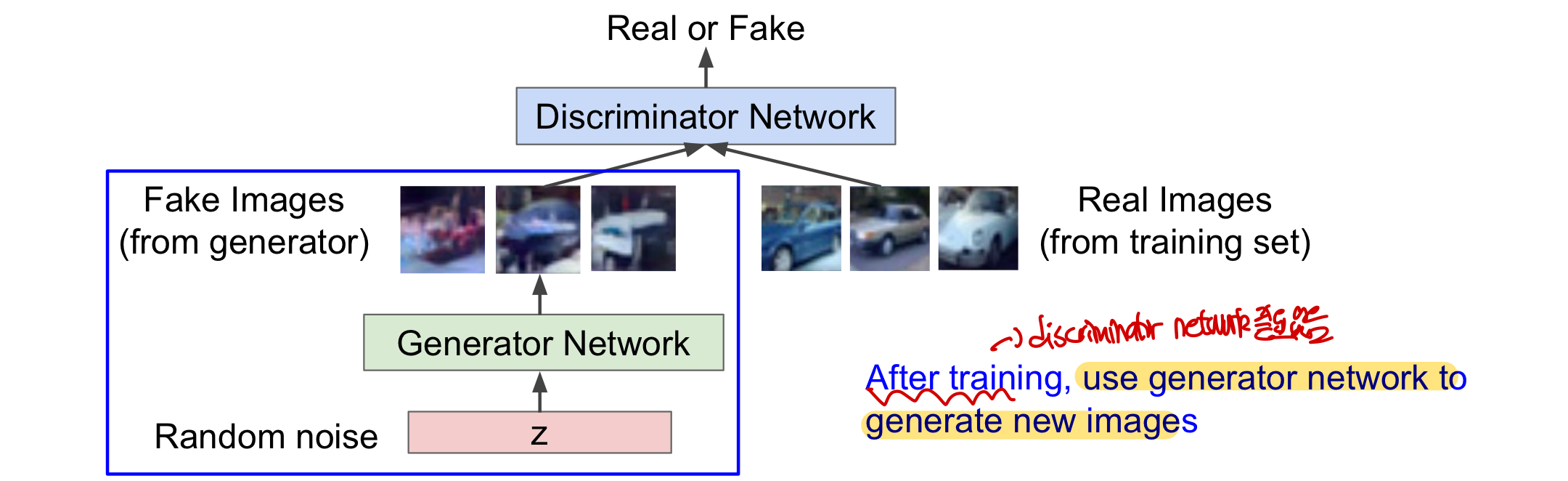
explicitly modeling density를 포기하고 그냥 sample을 하는 능력을 원함! (확률 분포를 명시적으로 정의하지 않고 그냥 sample을 하려고 함!) - 복잡하고 고차원의 training 분포로부터 sample을 하는 것을 목적으로 두는데 여기에서 바로 sample을 하는데에는 어려움이 있음(명시적으로 확률 분포를 만들기도 어려움) - 해결책: 더 단순한 분포에서 sampling하고 이 단순한 분포에서 우리가 원하는 학습 분포로 transformation하는 함수를 배움(by Neural network: 복잡한 transformation!) 게임이론을 가져옴!! (Two-player game) - Generator network: 실제와 비슷한 image를 generate를 하여 discriminator을 속이려고 함 - Discriminator network: 실제(training set)와 가짜(generator가 생성)한 image를 구분함 즉, generator은 discrminator을 속이기 위해 더 정교한 가짜 image를 만들도록 학습되고 discriminator은 실제와 가짜 image를 잘 구분하도록 학습된다. 여러 학습을 걸쳐 discriminator가 구분하지 못할 정도로 generator가 학습되면(성공률 50%) 이 generator network를 이용하여 image를 generate한다!

Training Gan

Minimax objective function: parameter에 따라 학습을 진행하는데, 이때 discriminator와 generator의 목표가 이 식의 값을 각각 최대화와 최소화하는데에 있음! 물론 결국 generator의 목표도 discriminator를 속이는데에 있기 때문에 식의 표현이 discriminator입장에 초점이 맞춰져 있긴 함 - D_theta_d(x): real data x에 대해 discriminator가 진짜라고 판단할 확률 - D_theta_d(G_theta_g(z)): feature z를 통해 generator에서 만든 image 대해 discriminator가 진짜라고 판단할 확률 discriminator 입장: D(x)가 1이 되고 D(G(z))가 0이 되도록하여 값을 최대화 하기를 원함 - 진짜 image에 대해서는 진짜라고 판단하며, 가짜 image에 대해서는 가짜라고 생각하도록 만드는 것 목표 - 결국 discriminator의 정확도를 높이는 것이 목표이기 때문에 gradient ascent를 함 generator 입장: D(G(Z))가 1이 되도록하여 이 식의 값을 최소화하려고 함 - discriminator가 가짜 image에 대해 진짜라고 생각하도록 만드는 것을 목표(정교한 가짜 image) - discriminator의 정확도를 줄이는 것에 목표이기 때문에 gradient descent를 진행 - 이 값이 낮아야 (D(G(z))가 높아야) discriminator가 fake image를 골라서 generator에게 좋음! 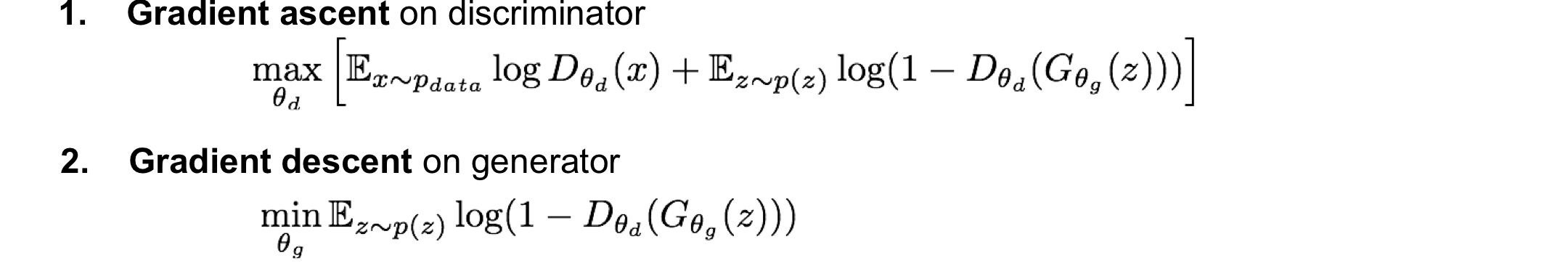문제점!: 이 generative입장에서의 optimize가 잘 진행되지 않음 in log(1-x) 그래프, x=D(G(z)) - x의 값이 낮을 때(DG(z)의 값이 낮음=discriminator가 가짜인걸 구분잘함=fake image인게 티남) gradient가 조금만 바뀌게 됨 - generator의 성능이 안좋아 많이 바뀌어야 함 - gradient가 많이 바뀌어야만 효율적인 학습이 가능함 - x의 값이 높을 때(DG(z)의 값이 높음=discriminator가 가짜인걸 구분못함=매우 정교한 fake image) 많이 바뀌게 됨 - generator의 성능이 이미 좋아 많이 바뀔 필요가 없음 - gradient가 조금 바뀌어야만 optimize가 잘됨 해결책: 관점을 바꿔 DG(z)의 값을 최대화시켜 generator의 gradient ascent를 진행 - discriminator가 맞을 확률을 최소화시키는 대신에 discriminator가 틀릴 확률을 극대화시킴 - 똑같이 generator가 discriminator을 속인다는 점에서 같지만 objective(목적)을 바꿔(flip) backpropagation에서 gradient ascent를 할때 훨씬 효율적log(x) : x=D(G(z)) - discriminator가 틀릴 확률이 적을때 (DG(z)값 낮음=discrimator가 적게 틀림=fake image인게 티남) gradient를 많이 바꿀 수 있게 됨 - discriminator가 틀릴 확률이 높을때 (DG(z)값 높음=discrimator가 많이 틀림=fake image인게 티안남) gradient를 조금만 바꿀 수 있게 되어 optimize가 더 잘 됨 참고: generator와 discriminator network를 동시에 training하는게 힘들고 불안정하기 때문에 더 나은 loss를 가지게 하는 하나의 목적을 가지고 training하는 것이 도움이 됨으로 generator에서 gradient ascent를 하는 것이 더 도움이 됨 GAN training algorithm discriminator에 대해서 train을 진행한 후에 generator에 대해서 train을 진행한다 - 이때 noise prior은 모델의 사전분포로, 노이즈나 불확실성에 대한 정보를 포함하는 분포 - noise prior에서 noise z를 뽑아 gradient를 통해 학습하면서 discriminator와 generator가 학습 - 이때 discrimnator을 학습시키는 횟수 k는 몇번을 해야할지 정확히 나와있지 않음 - 최근 Wasserstenin Gan에서 횟수 k에 대한 문제를완화했고 두개의 network를 balance할 필요가 줄어들었다고 함

After Training Gan

training이 끝난 후에는 generator network만을 이용해 새로운 image를 생성한다(discriminator network 필요 없음!) 이후 NN등을 이용해 sample을 generate할 수 있음 장점: 굉장히 정확도가 높고 멋있는 sample이 가능하다 단점: - 2개의 network를 directly하게 optimize하지 못하기 때문에 까다롭고 불안정함 - VAE에서의 문제점(intractable)이었던 p(x)나 p(z|x)에 대해 inference(추론)을 제공하지 못함 - p(x)값이 무엇인지 구하지 않고 그냥 sample한 것이기 때문에 믿음이 가지 않은 blackbox문제가 생길 수 있음 generator의 성능향상 Convolutional Architecture을 넣은 뒤 성능이 더욱 향상하게 되었다 - Generator: fractionally-strided convolution을 통한 upsampling CS231n 11. Detection & Segmentation (noise/feature z에서 새로운 이미지를 만들어야하기 떄문에 upsampling 필요) - Discriminator: convolutional network 이 모델에서 무작위로 2개의 latent variable을 뽑아 interpolating(두가지 사이의 중간값/ 부드럽게 이동, 전환하는 과정)을 보더라도 매우 정교하고 진짜같은 image를 뽑아낸다는 것을 알 수 있음 - 위에 VAE에서도 2개의 latent variable을 뽑아 비교한 것과 유사 - latent variable이 어떤 역할을 하는지 시각화해주는 것으로 생각할 수도 있을듯

Interpretable Vector Math CS231n 12. Visualizing and Understanding에서 했던 것처럼 숨겨져있는 latent variable이 실제로 어떤 역할을 하는지 이해하고 시각화해주는 역할을 하며 이 모델들도 사람들이 이해할만한 유의미한 과정을 가진다는 것을 알려주는 역할을 한다고 생각해볼 수 있을듯 이외에도 GAN은.. - 더 나은 training과 generation을 제공 - 높은 해상도를 제공 - 특정 부분을 원하는 부분으로 바꾸는 기능 제공 - text를 통해 새로운 image를 생성하는데 제공