매우 중요!! https://youtu.be/kYB8IZa5AuE?si=KGPRHdV1GH4iqbI6 #linear_transformationmatrix
⭐️ matrix(행렬)를 볼때마다 공간의 어떠한 transformation이라고 생각해야함! ⭐️
Linear transformation
공간을 이동시키는 방법, 공간을 이동시키는 와중에 basis vector의 변환을 이용해 얻은 좌표를 통해 다른 vector들이 어떻게 변화하는지를 보여주는 함수라고 생각하면 됨!
transformation
transformation을 그냥 입력이 들어오면 출력은 내보내는 함수(function)라고 생각하면 된다.
- 입력으로 vector가 들어오면 출력으로 vector가 나오게 됨
- 그럼 왜 function이 아니라 transformation이라고 할까?
- 입력에서 출력으로의 movement 변화를 시각적으로 표현하기 위해
- vector을 이해하는 가장 좋은 방법은 움직임!(이동시키는 것으로 생각!)
Linear Algebra 2. Linear combination, span and basis vectors 여기서 나온 여러가지 vector을 표현할 때는 점으로 생각하라는 아이디어를 이용하며 input vector가 tranformation되어 output vector가 되는 것을 점을 이용하면 쉽게 생각 가능하다
Linear
여러가지 형태로 vector의 점들이 transformation 될 수 있지만 여기서는 오직 linear한 형태의 변형만 고려!
- transformation 이전과 이후에도 모두 모든 방향에서 직선이어야만 함(휘면 안됨)
- 원점(origin)은 변환 이후에도 원점이어야함
- 이때 grid line들이 모두 parallel하고 evely spaced(동일 간격)여야함
이러한 transformation을 수치적으로 어떻게 설명할 수 있을까?
두개의basis_vector 만 어떻게 변하는지만 알면 설명이 가능하다. transformation 이전의 linear transformation이 이후의 transformation까지 유지가 되는데 이는 grid line들이 여전히 parallel & evenly space한 특성을 가지기 때문이다. 그렇기 때문에 basis vector의 변형위치만 알게 되면 새로운 vector v를 추론 가능
이렇게 되면 어떤 vector이든지 변환후에 어디로 이동할지 알아낼 수 있게 된다. 식을 이용하여 일반화 가능하며 아래 사진의 경우 vector의 위치는(1x+3y,-2x+0y)가 된다. 즉, 어떤 임의의 vector x,y에 대해서 위치가 어디인지 결과 vector을 알 수 있다
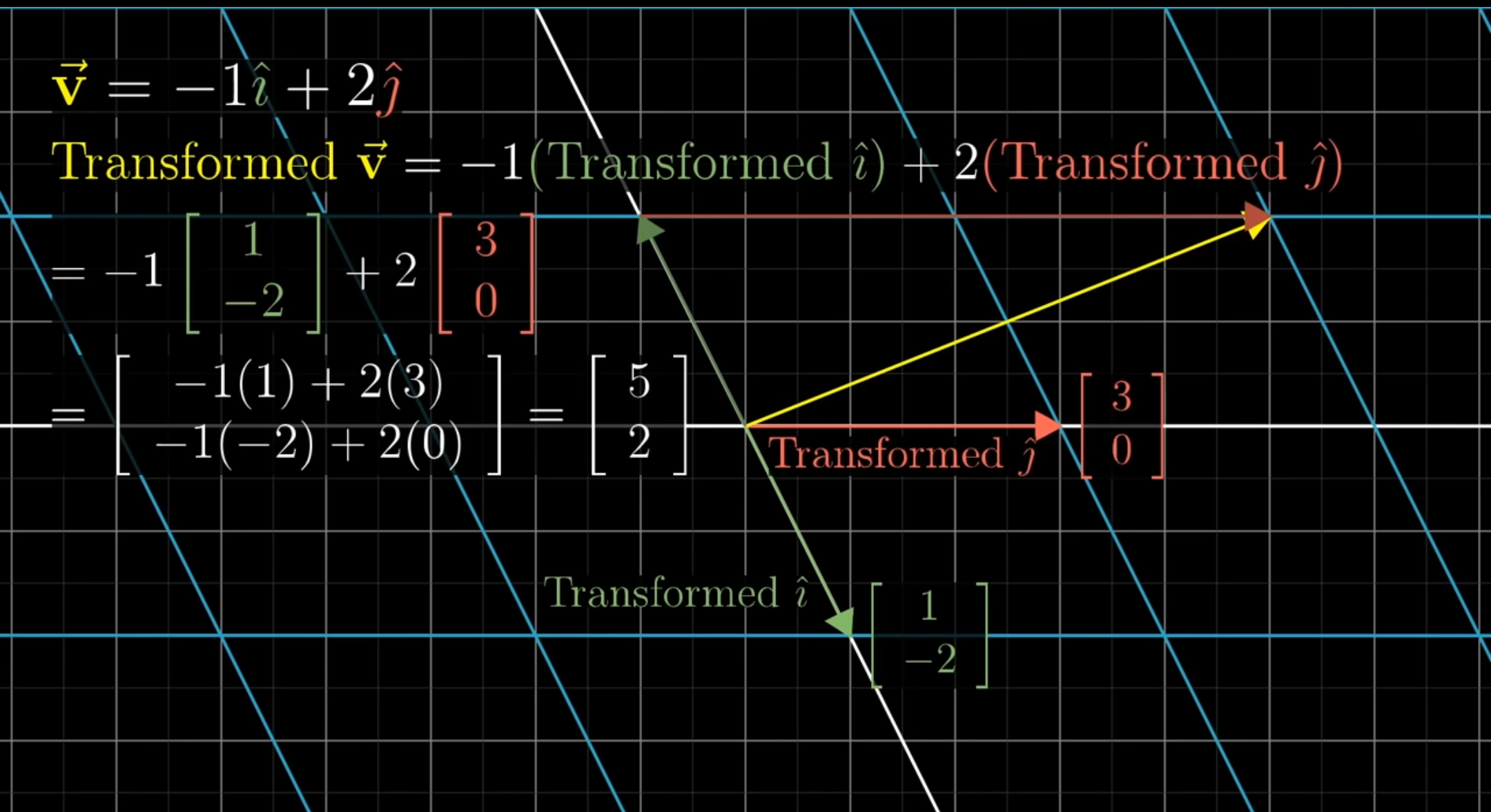
Matrix
행렬은 위에서 언급한 transformation을 설명하는 언어로 matrix는 단지 계산하는방법이라고 보면 된다. 2차원에서 4개의 수(각각의 basis에 transformed 후의 좌표!)로 모든 vector가 표현 가능하다.
matrix에서 각각의 열이 basis vector가 transformation후 land한 vector의 위치를 나타낸다.
- 새로운 vector가 주어졌을 때,matrix와 연산될 경우 어디로 변환시키는지 보여주는 사진!
- 기존의 transformed basis vector을 다른 vector의 값만큼 scaling 후 더하여 변환된 곳을 알려준다
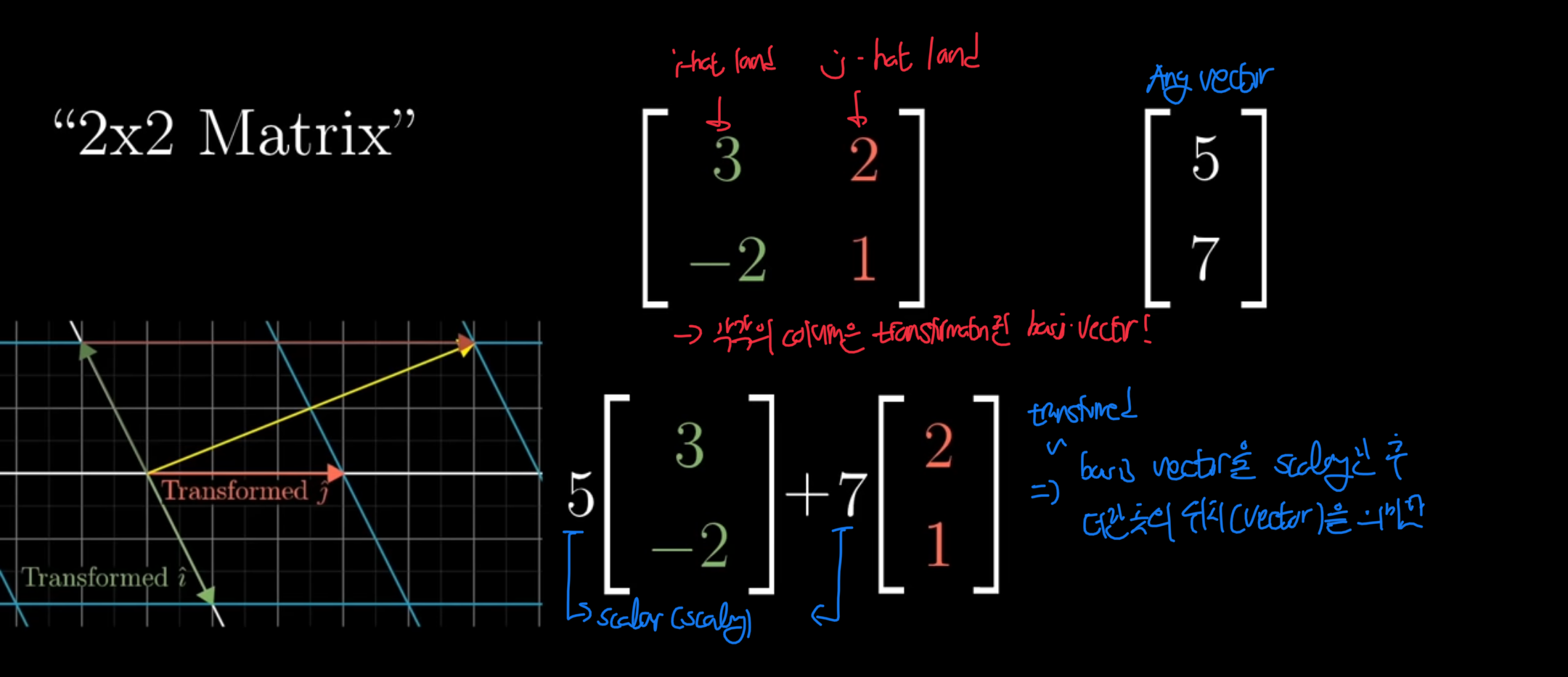
두 transformed basis vector가 linearly dependent이면?
A: vector 하나가 다른 vector의 scaling 버전임 = 2차원 공간을 squish(수축)시켜 두 vector가 놓여있는 선으로 만듦