DDQN(2015) Deep Reinforcement Learning with Double Q-learning

0. Introduction

Summary

Q-learning : 과대평가(overestimation)이 존재 ➡️ 그럼 과대평가가 나빠? 🙋‍♀️일정하면 괜찮은데 일정하지 않으면 나빠(policy에 악영향) ➡️ 그럼 DQN은 과대평가(overestimation) 문제가 있어? 🙋‍♀️ 있다! 그래서 새로운 DDQN 알고리즘을 만들었고 실제 성능 향상이 생김 ‼️과대평가(overestimation)이 줄어들면 policy의 성능이 향상되는구나!

Q-learning 알고리즘은 특정 조건에서 action 값에 대해 과대평가하는 것으로 알려져 있는데, 이러한 특성은 성능을 악화시키며 실제로 DQN에서 과대평가(overestimation)이 진행된 것을 확인하였다. 이 논문에서는 Double DQN이라는 알고리즘으로 overestimation을 줄일 뿐 아니라 몇몇 게임에서 훨씬 나은 성능을 보인다는 것을 보인다.

1989년엔 나온 Q-learning은 action값들을 평가할 때 maximization을 진행하기 때문에 비현실적으로 높은 action값을 학습하게 되고 van Hasselt,2010,2011 논문들을 통해 정확하지 않는 approximation error이라는 조건일 때 overestimation을 보인다는 것을 보인다.

그렇다면 과대평가(overestimation)이 나쁠까? 만약 모든 값들이 일정하게 증가한다면 상관이 없을 뿐더러 exploration (탐험)을 통한 학습을 위해 과대평가(overestimation)은 좋을 수 있다. 하지만 과대평가가 일정하지 않고 우리가 학습하기를 원하는 state의 값이 낮게 나올 떄는 policy의 결과에 부정적인 영향을 준다.

그렇다면 DQN(2015) Human-level control through deep reinforcement learning에 나온 DQN은 과대평가(overestimate) 문제를 가지고 있을까? 이 논문에서 알아본 병가 DQN은 action의 값을 상당히 과대평가 하고 있다. 이에 따라 Double DQN 알고리즘을 만들었으며 값을 평가(estimate)할 때 더 정확할 뿐 아니라 더 높은 점수를 얻음으로써 ,overestimation이 policy의 성능 악화를 낳고 이것을 줄이는 것이 중요하다는 것을 강조한다.

1. Background

Q-learning과 DQN에 대해서는 CS231n 14. Deep Reinforcement Learning와 DQN(2015) Human-level control through deep reinforcement learning을 참고하면 된다. 간단히 설명을 하자면 가장 최적의 action의 값을 찾는 과정이 Q-learning이고, bellman equation을 통해 그 다음 state에서 가장 많은 reward를 받을 것으로 예상되는 action을 취하면서 update하게 된다. DQN은 너무 많은 action과 state 때문에 네트워크의 parameter $\theta$를 이용해 학습을 하며 특히 위 논문에서는 experience replay와 τ step마다 복사가 되는 target network를 구성하여 알고리즘의 성능을 높였다.

Q-learning과 DQN의 문제는 action을 고르고 평가할 때 같은 값을 선택하게 되고, 이것이 더욱 과대평가(overestimate)한 결과를 가져온다. 이것들 막기 위해서는 고를 때와 평가하는 값을 따로 뽑아야하며(decouple) 이는 Double Q-learning의 아이디어를 통해 해결이 가능하다.

Double Q-learning은 2개의 value function($\theta ,{\theta }^{\prime }$)을 학습시키며 이때 각각의 experience들은 무작위하게 2개의 value functon 중 하나로 들어가 업데이트를 진행하게 된다. 각각의 업데이트마다 하나의 weight(function)는 policy를 결정(select)하고 다른 하나의 weight는 그것의 값을 결정(evaluate)한다. 이렇게 되면 Q-learning의 selection과 evaluation을 다음과 같이 풀어쓸 수 있다.

• target: $Y_t^Q=R_{t+1}+\gamma Q(S_{t+1},argma{x}_{a}Q(S_{t+1},a;{\theta }_t);{\theta }_t)$
• ⭐️ error: $Y_t^{DoubleQ}=R_{t+1}+\gamma Q(S_{t+1},argma{x}_{a}Q(S_{t+1},a;{\theta }_t);{\theta }_t^{\prime })$

⭐️⭐️ 여기서 action은(argmax) 현재의 가중치 $\theta$에 대해 선택이 되며 이는 곳 현재의 value에 따라 가장 가치있는 것으로 추정되는 policy를 선택한다는 것이다. 하지만 두번째 weight ${\theta }^{\prime }$를 통해 policy의 값을 평가하여 공정하고 과대평가(overestimate)를 줄일 수 있다. 또한 $\theta ,{\theta }^{\prime }$의 역할을 바꾸어가면서 업데이트하여 서로 학습이 가능하도록 만든다.

2. Overoptimism due to estimation errors

과대평가(overestimation) 문제는 Thrun and Schwartz(1993)이 처음 제기했으며 각각의 target은 error가 ($-ϵ,ϵ$)에 균일하게 분포되어있을 때, 최대 $\frac{m-1}{m+1}$까지(m은 action의 수) 과대평가 될 수 있으며 최적화가 되지 않을 수 있다고 주장했다. 이후 van Hasselt가 environment의 noise가 과대평가를 만들 수 있으며 Double Q-learning을 통해 해결 가능하다고 주장했다. 이 부분에서는 어떠한 종류의 평가오류(estimation error)이든지 간에 상방편향(upward bias)를 만들 수 있음을 강조한다 (van Hasselt가 주장한 enviornment의 noise 이외에도 다수히 실제 값들을 몰라서 생기는 error들도 과대평가를 만들 수 있음!)

Theorm: Q-learning 방식은 lower-bound가 존재

Thrun and Schwartz와는 다르게 과대평가의 상한선이 아닌 하한선이 있음을 증명하여 기존의 DQN이 어떠한 경우든 error가 존재해 과대평가가 존재함을 보여주고자 한다

Theorm1

가정(Assumption)

1. $Q_{\ast }(s,a)=V_{\ast }(s)$: state s에서 어떤 action을 하든지 optimal Q값은 갖다고 가정하며 이때는 s,a에 대한 식이 아닌 s에 대한 식이 됨
2. ${\sum }_a(Q_t(s,a)-V_{\ast }(s))=0$: 모든 bias들의 합이 0이라고 가정(단, 모든 bias들이 0은 아니다!)
3. $\frac{1}{m}{\sum }_a(Q_t(s,a)-V_{\ast }(s){)}^2=C$ :이때 C>0이며 action m≥2이다 결론(Conclusion)

• $ma{x}_a{Q}_t(s,a)\ge V_{\ast }(s)+\sqrt{\frac{C}{m-1}}$
• 즉, 1,2,3번 가정을 만족할 때 error가 최소 $\sqrt{\frac{C}{m-1}}$만큼 생기며 lower bound가 존재하며 이에 반해 Double Q-learning의 lowerbound는 0이다.

이 Theorm은 가치추정(value estimate)가 1. 가장 이상적인 경우라고 하더라도 (모든 가치추정 값이 평균치일 때) 실제 optimal 값과 차이가 생기며 이로 인해 lowerbound가 생긴다는 것을 보여준다. 2. 하나의 맹점은 위의 theorm의 결론이 action이 증가할 수록 lower bound가 줄어든다는 것인데, 실제로는 action이 증가할 수록 과대평가가 증가한다. 즉, 일종의 인위적 오류(artifact)이며 lower bound가 낮아졌다고 해서 꼭 과대평가가 낮아져야 하는 것은 아닌 것이라고 생각하면 될 듯하다 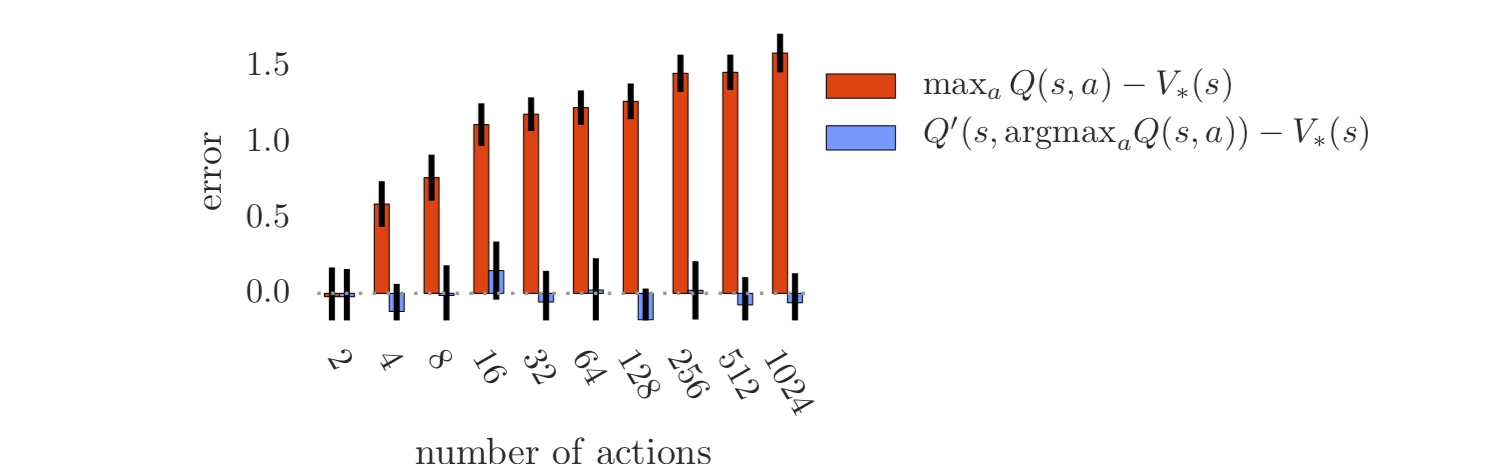또 다른 예로, 위에 Thrun and Schwartz가 쓴 내용을 빌리지마녀 action의 수가 m개 일 때 overoptimisim은 $\frac{m-1}{m+1}$을 따르며 이는 곧 action의 수가 많아질 수록 과대평가가 커진다는 것을 의미한다.

Proof

Experiment : lowerbound 있음을 증명

위에서는 수학적으로 Q-learning의 실제 값과 optimal하다고 생각하는 추정값 사이의 error가 존재한다는 것을 증명했는데, 이를 실제 값(true value)을 알고있는 함수를 이용해 Q-learning으로 학습하여 실제 lowerbound가 존재하는지를 직관적으로 보인다. 이때 총 3가지 함수를 사용하여 여러가지 결과를 도출한다

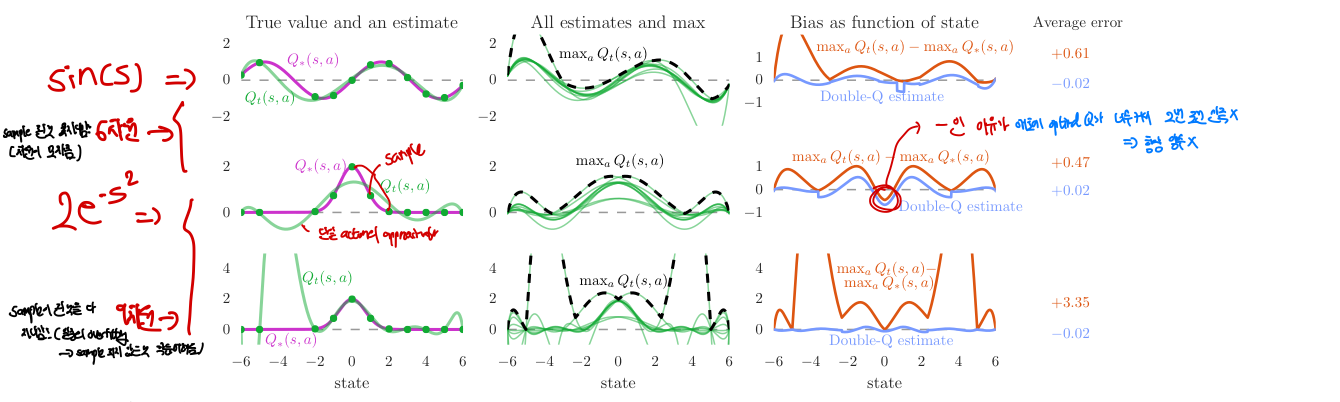
• 초록색 선: 여러 실제 state들을 sample해서 추정된 $Q_t(s,a)$값= 상태(state)가 변함에 따라 한 행동(action)에 대해 예측된 가치가 어떻게 변하는지를 보여줌
• 분홍색 선: 실제 true value들, optimal $Q_{\ast }(s,a)$

맨 왼쪽 사진: 간편성을 위해 theorem에서의 1번 가정: 한 state에서의 모든 action의 ptimal 값은 동일하다는 것을 이용한다. 더불어 true value들의 분포는 간단히 표현할 수 있는 함수($Q_{\ast }(s,a)=\sin (s),-2\exp (-s^2)$)를 사용하고 이 분포에서 값들을 sample한 estimate를 초록색 점으로, 이들을 통해 근사한 state function을 초록색 선으로 표기하였다. 이때 sample들은 정확히 실제 분포에서 뽑았으며, 위 2개의 행은 6차원, 가장 아래 행은 9차원으로 sample을 통해 estimate function을 학습했다.

• 맨 위 2개 행은 제대로 근사(approximation)을 하지 못함 ⇒ 함수의 차원이 낮아서 충분히 학습을 못함
• 가장 아래행은 제대로 근사할 만큼 차원이 높고 유연(flexible) 했지만 오히려 이것이 sample되지 않은 state들에 대한 정확도를 낮춤
• sample state들이 멀리 떨어져있을 수록 estimation error가 증가하며 이것은 우리가 RL에서 몇개를 sample해서 제한적인 값만을 아는 것처럼 매우 일반적인 경우이다

중간 사진:

3. Double DQN

4. Empirical results

5. Conclusion